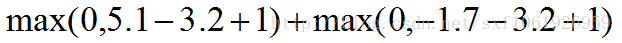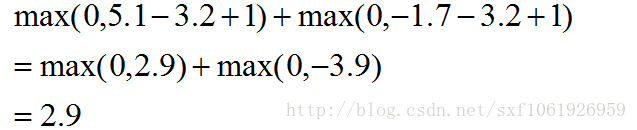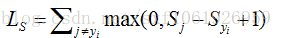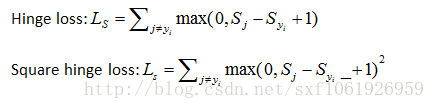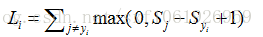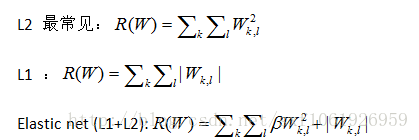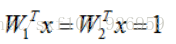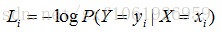hinge loss/支援向量損失的理解
線性分類器損失函式與最優化
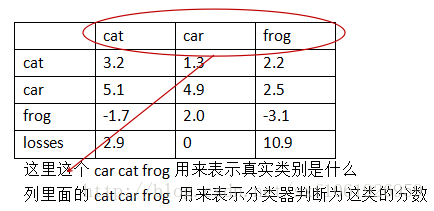
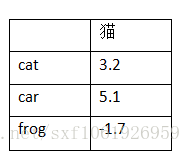
假設有3類 cat car frog
第一列第二行的5.1表示真實類別為cat,然後分類器判斷為car的的分數為5.1。
那這裡的這個loss怎麼去計算呢?
這裡就要介紹下SVM的損失函式,叫hinge loss。
如上圖所示,我們去計算第一列的損失,計算方法如下:
因為真實的類為cat,所以我們讓其他兩類的分數去減去真實類的分數,相當於去計算真實類和其他類之間的誤差。得到第一列的誤差計算如下:
- 1
- 2
這裡3.2為真實類的分數,所以為被減數。
這個計算方法就是用的多類SVM損失。
SVM損失(hinge loss)
給定一個樣本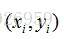
這是一個二分類支援向量機的泛化,它計算了所有不正確的例子,將所有不正確的類別的評分,與正確類別的評分之差加1,將得到的數值與0作比較,取兩者中的最大值,然後將所有的數值進行求和。
我們不僅要使得正確類別的評分高於錯誤類別的評分,還使用了一個安全係數,係數的值為1,為啥安全係數為1?
根據W的不同,得出的分數也不同,W按比例縮放,分數也在縮放,所以安全係數為1是隨意給的。
全部訓練集的Loss是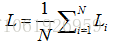
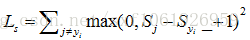
問:那麼利用hinge loss的最大損失和最小損失分別為多少?
答:最小值:0,最大值:無窮大
問:最開始的時候,W都很小,接近於零,那麼在優化的時候分數很接近零,就是說左邊計算出的Sj都接近零,那麼損失值會怎麼樣?
答:像左邊只有三類的,平均損失會接近2。
正確性檢查程式
一般為了正確性檢查程式,當從很小的數W開始優化時,你的第一個損失函式,如果你的函式形式基本正確,只需要去看得到的數是否有意義,例如當在這個例子中損失為2,說明程式正確執行。
向量化實現:
Def Li_vecterized(x,y,W):
Score =W.dot(x)
Margins = np.maximum - 1
- 2
- 3
- 4
- 5
- 6
問:如果我們找到了一個W,使得損失函式為零,那麼這個W是否是獨一無二的?
答:當找到一個W後,用2W去計算Loss,發現損失還是為零,而且越大,分數越大,差本來就是小於-1的數,那更加小於-1
所以引入了正則化 R(W)
正則化
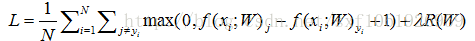
R(W)衡量了W的好壞,我們不僅僅想要資料擬合得更好,也希望能優化W,訓練損失和你用於測試集的泛化損失,所以正則化是一系列通過損失來使目標相加的技術,和前面的項形成競爭,前面的想適應你的訓練資料,而這個想要讓W呈現一種特殊的方式,所以有時在目標中他們會相互競爭。
事實證明,正則項有時會讓訓練錯誤變得更多,甚至造成錯誤的分類,但是我們注意到,他會使測試結果表現得更好。
常見正則化或者權值衰減:
還有max norm /drop out等
例:
X=[1,1,1,]
W1 = [1,0,0,0]
W2 = [0.25,0.25,0.25,0.25]
他們乘積都為1:
不加正則化,分數一樣,loss一樣,但L2正則化考慮了x中的大部分東西,L2會認為W2好些。
Softmax
Softmax分類:一般化的邏輯斯蒂迴歸
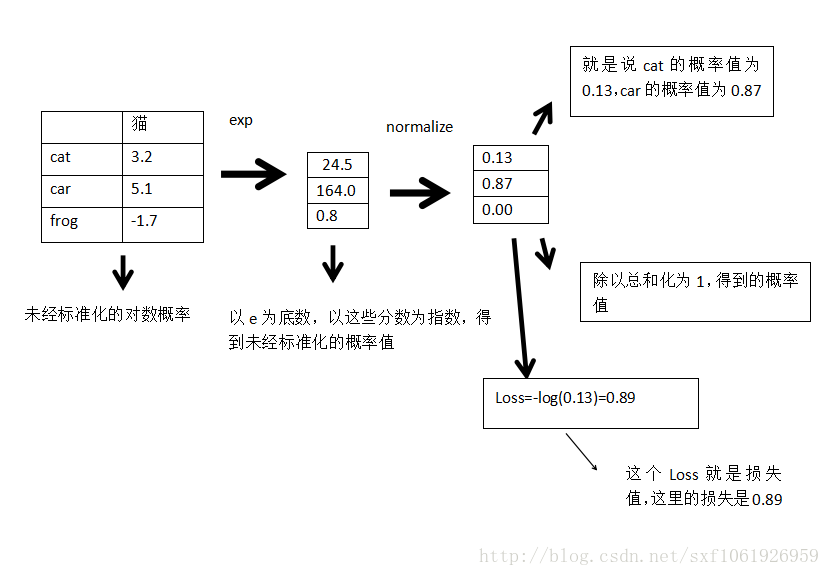
假設這些分數都是未標準化的對數概率
這一列表示真實圖片為貓,然後判斷為這三類的分數分別為3.2、5.1、-1.7。
求圖片為某一類的概率: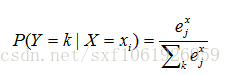
使正確分類的概率的對數最大,根據損失函式,我們要使負的正確分類概率的對數最小,所以概率對數是分數的擴充套件。
問:上面這個Loss的最大值、最小值?
答:看log函式就能看出來,為1的時候最小為0,為0的時候最大為無窮大。
問:剛開始訓練的時候,W很小,那麼損失值是多少呢?
答:是類別數分之一的對數負值,可用於檢查程式碼
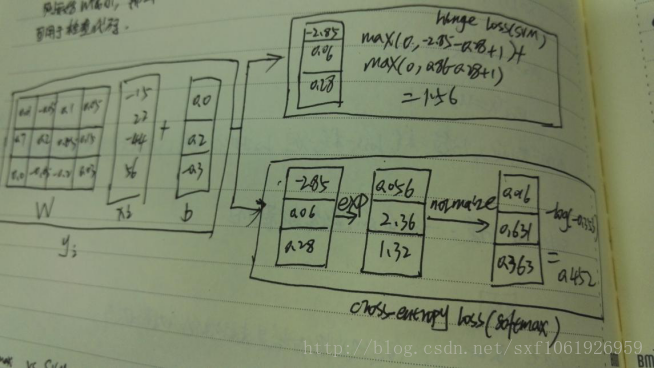
Hinge loss和cross-entropy loss比較
下圖分別展示了hinge loss和cross-entropy loss的計算過程。
Hinge loss的話只有當分類正確,即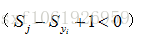
但是cross entropy loss對每個樣例的每個分數都有用到。當分數發生微小變化的時候,cross entropy loss會變,hinge loss不會變。
下一章 反向傳播與神經網路初步
原文地址:http://blog.csdn.net/sxf1061926959/article/details/60470415