多普勒微波感應和FMCW微波感應原理以及應用
0. 前言
雷達主要分為多普勒雷達、脈衝雷達、頻率調製連續波FMCW雷達。脈衝雷達由於需要貴重的磁體控制脈衝開關,較少使用。多普勒雷達通常只能獲得目標速度,而目標距離難以獲取。FMCW雷達,
1. 多普勒雷達HB100原理
多普勒雷達原理來自多普勒效應。手頭上的HB100微波感測器的原理是多普勒測距雷達。規格書上[1]有本模組的方框圖。

設傳送訊號為T(t),則其函式為:
是傳送訊號的頻率。多普勒雷達中這個頻率一般是個固定值。
是初始相位。
不計天線增益和訊號衰減,接收天線的獲得的訊號為:
其中是傳送訊號的波長。
。c是光速,約為3x10^8m/s。v是目標的移動速度。
Mixer是T(t)和R(t)的相乘。
根據三角函式關係:
可得:
採用合適截止頻率的低通運放電路,即截止頻率在,可以得到輸入到ADC模組的訊號:
公式中G是運放的增益。模組的規格書說明,輸出訊號電壓幅值和成正比的。
2. HB100的典型應用
規格書[1]有HB100的典型應用,根據此圖,在KiCad上可以繪製出原理圖。KiCad的原理圖和PCB設計檔案已經共享到github。https://github.com/xxJian/HB100_Microwave_Demo

R1作用是假負載。
靜態分析:
V1out中由於U2A運放對直流訊號沒有放大作用,同時沒移植作用,故VCC增益不變。
動態分析:
1階RC電路截止頻率計算公式:
| 電阻 | 電容 | 截止頻率 |
| R5+R2//R3 |
C2 |
0.09Hz |
| R4 |
C5 |
3.39Hz |
| R6 |
C6 |
72.34Hz |
| R7 |
C8 |
4.13Hz |
| R8 |
C9 |
72.34Hz |
| R9 |
C10 |
16KHz |
3. FMCW雷達
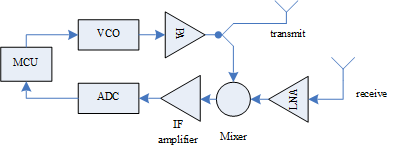
圖2. 一款雷達應用的實現框圖[5]
MCU是微控制器。VCO是壓控振盪器,可以通過輸入的模擬訊號大小而控制輸出訊號的頻率。PA是功率運放。LNA是Low Noise Amplifier的縮寫。Mixer把兩個訊號相乘並輸出IF訊號。IF amplifier是把IF訊號放大,並帶有低通濾波的效果。ADC是模擬訊號-數字訊號轉換器。
單傳送單接收的FMCW示意圖如圖3所示。FMCW調製過程中,線性調製訊號的上限和下限只差為B,同時這個頻率範圍有嚴格規定[2]。24GHz雷達的頻寬為200MHz,而77GHz允許有4GHz的頻寬範圍。
3.1 計算距離
傳送訊號的頻率為ft。fr為接受訊號的頻率。Td是傳送、接收延時。Tc為上升時間。線性調製的斜率為B/Tc。

圖3 FMCW示意圖
圖3中,由相似三角形,可得到以下關係:
而
傳送訊號的波形函式(Tc時間內):
而接收訊號的時域函式:
混頻器的輸出時域函式(這裡就直接頻率相減、相位相減):
通過FFT得到Mix(t)的頻率,再通過計算即可得到距離d。
3.2 計算速度
時間間距為Tc,先後傳送兩個線性調製脈衝訊號,見下圖。

傳送訊號的波形函式(Tc時間內):
適當化簡:
那麼接收訊號的時域函式是:
適當化簡:
混頻器輸出:
將Mix1和Mix2再次進行混頻(頻率相減、相位相減)
4. TODO: TI的mm radar
到TI的官網搜mm radar得到iwr1443 mmware radar……個人認為資料比較豐富了。還有教學視訊,但我還沒看。
參考資料:
資料[1]:https://www.limpkin.fr/public/HB100/HB100_Microwave_Sensor_Application_Note.pdf
資料[2]:Moving from legacy 24 GHz to state-of-the-art 77 GHz radar, http://www.ti.com/lit/wp/spry312/spry312.pdf
資料[3]:MicrowaveNoncontactMotionSensingandAnalysis.pdf
資料[5]:http://hforsten.com/third-version-of-homemade-6-ghz-fmcw-radar.html
