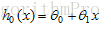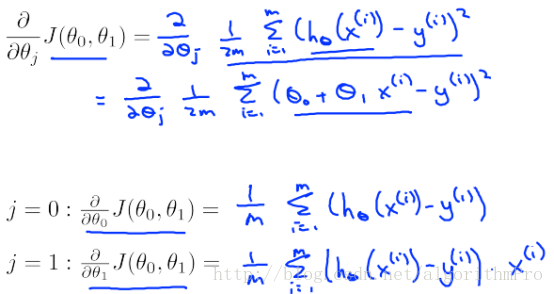單變數的線性迴歸模型演算法
阿新 • • 發佈:2018-11-09
【寫在前面的話】大概一年前看過Andrew老師的機器學習課程,受益良多。今年在用機器學習分類的時候,發現很多機器學習基礎知識都已經忘得一乾二淨,對自己很是無語。因此,作者打算重新溫習一篇Andrew老師的機器學習課程,並用部落格來記錄每一節課程的知識要點,加油吧!
機器學習模型:
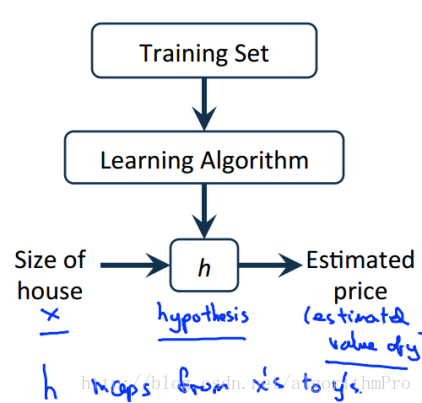
如上圖,機器學習可以理解為:通過對訓練資料學習來構建模型h(
模型估計:
模型估計主要是通過最小化損失函式來實現的,因此,怎麼找到損失函式且最小化損失函式是模型估計的重點。
假設單變量回歸模型:
損失函式(cost function):
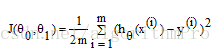 ,其中i為樣本序號。
,其中i為樣本序號。
通過最小化損失函式來求解模型引數,如下圖:

梯度表示某一曲面在該點處增加最快的方向,因此,梯度的反方向亦是數值減小最快的方向,梯度下降法來求極值即是利用了這一種思想。
梯度下降演算法:

利用梯度下降法同時更新theta0和theta1,當值隨著迭代次數的增加收斂時,則停止更新,記錄當前的引數值。
如上圖:α代表學習率,若α過小,則梯度下降演算法運算時間較慢;若α過大,則梯度下降演算法則會超過極小值,最後可能不能滿足收斂,甚至發散。
上表表示:固定學習率α,也能達到極小值,因為越接近極值點,則梯度越小,移動步長會自適應的較小。
梯度下降演算法求解線性迴歸

通過梯度下降演算法同時更新引數

梯度下降演算法的求解受到初始值的影響,初始值選取的不一樣,最後得到的結果有可能不一樣,如下兩圖:
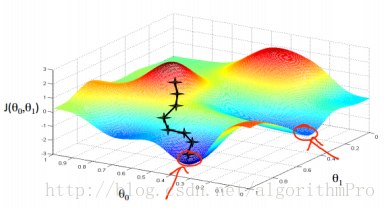

也可用等高線來表示:

損失函式可以理解為凸函式(convex Function),如下圖:

批量梯度下降演算法:
批量:每個步驟的梯度下降演算法都使用了全部的訓練資料。