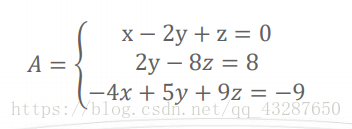numpy.linalg模組包含線性代數的函式。使用這個模組，可以計算逆矩陣、求特徵值、解線性方程組以及求解行列式等。

一、計算逆矩陣

語法：np.linalg.inv()

import numpy as np#匯入模組
# 準備一個矩陣
a = np.mat('0 1 2;1 0 3;4 -3 8')
#計算逆矩陣
a_inverse = np.linalg.inv(a)

a*a_inverse #驗證A* A-1 =I 是否成立

得到對角方陣，成立
matrix([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])

二、解線性方程組

語法：np.linalg.solve()

已知線性方程組：

求x,y,z

#根據方程組係數準備一個矩陣
b = np.mat('1,-2,1;0 2 -8;-4 5 9')

# 建立結果的！！！！陣列
value = np.array([0,8,-9])
value

array([ 0,  8, -9])

x,y,z = np.linalg.solve(b,value)
print(x)
print(y)
print(z)

29.0
16.0
3.0

三、特徵值和特徵向量

語法：np.linalg.eigvals() np.linalg.eig()
eigvals 函式可以計算矩陣的特徵值
eig 可以返回一個包含特徵值與特徵向量的元組

c = np.mat('3 -2;1 0')

#特徵值
np.linalg.eigvals(c)

array([2., 1.])

#特徵值和特徵向量
np.linalg.eig(c)

(array([2., 1.]), matrix([[0.89442719, 0.70710678],
         [0.4472136 , 0.70710678]]))

補充一小點特徵值和特徵向量的知識點：
定義：

解特徵值和特徵向量:

四、奇異值分解

語法：np.linalg.svd()
在numpy.linalg模組中的svd函式可以對矩陣進行奇異值分解。該函式返回3個矩陣——U、Sigma和V，其中U和V是正交矩陣，Sigma包含輸入矩陣的奇異值。

d = np.mat('4,11,14;8,7,-1') #準備一個矩陣

u,sigma,v = np.linalg.svd(d,full_matrices=False) #這個引數很重要，但是我不知道是什麼

u

matrix([[-0.93684246, -0.34975164],
        [-0.34975164,  0.93684246]])

sigma

array([19.19547799,  8.86191992])

v

matrix([[-0.34098567, -0.66440276, -0.66505469],
        [ 0.68785693,  0.3058738 , -0.65825076]])

np.diag(sigma) #變成斜角的2*2矩陣

array([[19.19547799,  0.        ],
       [ 0.        ,  8.86191992]])

u*np.diag(sigma)*v #驗證奇異值，返回d

matrix([[ 4., 11., 14.],
        [ 8.,  7., -1.]])

5.計算矩陣的行列式

語法：np.linalg.det()

e = np.mat('3 4;5 6')

np.linalg.det(e)

-2.0000000000000004