C. Read Time

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Mad scientist Mike does not use slow hard disks. His modification of a hard drive has not one, but n different heads that can read data in parallel.

When viewed from the side, Mike's hard drive is an endless array of tracks. The tracks of the array are numbered from left to right with integers, starting with 1. In the initial state the i

-th reading head is above the track number hi. For each of the reading heads, the hard drive's firmware can move the head exactly one track to the right or to the left, or leave it on the current track. During the operation each head's movement does not affect the movement of the other heads: the heads can change their relative order; there can be multiple reading heads above any of the tracks. A track is considered read if at least one head has visited this track. In particular, all of the tracks numbered h1, h2, ..., hn have been read at the beginning of the operation.

Mike needs to read the data on m distinct tracks with numbers p1, p2, ..., pm. Determine the minimum time the hard drive firmware needs to move the heads and read all the given tracks. Note that an arbitrary number of other tracks can also be read.

Input

The first line of the input contains two space-separated integers n, m (1 ≤ n, m ≤ 105) — the number of disk heads and the number of tracks to read, accordingly. The second line contains n distinct integers hi in ascending order (1 ≤ hi ≤ 1010, hi < hi + 1) — the initial positions of the heads. The third line contains m distinct integers pi in ascending order (1 ≤ pi ≤ 1010, pi < pi + 1) - the numbers of tracks to read.

Please, do not use the %lld specifier to read or write 64-bit integers in С++. It is recommended to use the cin, cout streams or the %I64d specifier.

Output

Print a single number — the minimum time required, in seconds, to read all the needed tracks.

Examples

input

Copy

3 4
2 5 6
1 3 6 8

output

Copy

2

input

Copy

3 3
1 2 3
1 2 3

output

Copy

0

input

Copy

1 2
165
142 200

output

Copy

81

Note

The first test coincides with the figure. In this case the given tracks can be read in 2 seconds in the following way:

1. during the first second move the 1-st head to the left and let it stay there;
2. move the second head to the left twice;
3. move the third head to the right twice (note that the 6-th track has already been read at the beginning).

One cannot read the tracks in 1 second as the 3-rd head is at distance 2 from the 8-th track.

官方題解：

343C - Read Time

Let's search the answer t with the binary search. Fix some value of t. Look at the first head from the left h[i] that can read track p[0]. If p[0] > h[i], then h[i] goes to the right t seconds and reads all tracks on its way. Otherwise if p[0] ≤ h[i], then the head has two choices:

1. go to the right 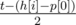 seconds, then  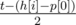to the left and h[i] - p[0] again to the left;
2. go to the left h[i] - p[0] seconds, then h[i] - p[0] to the right and t - 2·(h[i] - p[0]) again to the right.

Obviously, for h[i] it is more advantageous to visit the track positioned as much as possible to the right. So we choose by 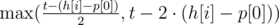. Then we move the pointer onto the first unread track, and repeat the algorithm for h[i + 1], and so on with each head.

Solution complexity: .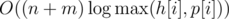 

#include <cstdio>
#include <cstring>
#include <algorithm>
#include<iostream>
using namespace std;
typedef long long LL;
const int  maxn = 1e5+10;
const LL INF=1e18;
LL h[maxn],p[maxn];
bool vis[maxn];
int n,m;
bool check(LL mid){
    int step=0;
    for(int j=0;j<n&&step<m;j++){
        if(h[j]-p[step]>mid)
            return false;
        LL s=h[j];
        if(p[step]<=s){
            //向左走，然後向右走的最大值
            s=max(s,mid-(h[j]-p[step])+p[step]);

            //向右走，然後向左走的最大值
            s=max(s,(mid-(h[j]-p[step]))/2+h[j]);
        }else{
            //如果左邊沒有要訪問的點，直接向右走
            s=h[j]+mid;
        }
        while(step<m&&p[step]<=s)   step++;
    }
    return step>=m;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=0;i<n;i++)
        scanf("%I64d",&h[i]);
    for(int i=0;i<m;i++)
        scanf("%I64d",&p[i]);
    LL left=0,right=INF;
    while(left<=right){
        LL mid=(right+left)>>1;
        if(check(mid))
            right=mid-1;
        else
            left=mid+1;
    }
    printf("%I64d\n",left);
}