內容提要

• 特徵選擇概述
• 常見模型
• 文件頻率(DF)
• 卡方校驗(CHI)
• 資訊增益(IG)
• 互資訊(MI)

特徵選擇概述

  在向量空間模型中，文字可以選擇字、片語、短語、甚至“概念”等多種元素表示。這些元素用來表徵文字的性質，區別文字的屬性，因此這些元素可以被稱為文字的特徵。在文字資料集上一般含有數萬甚至數十萬個不同的片語，如此龐大的片語構成的向量規模驚人，計算機運算非常困難。進行特徵選擇，對文字分類具有重要的意義。特徵選擇就是要選擇那些最能表徵文字含義的片語元素。特徵選擇不僅可以降低問題的規模，還有助於分類效能的改善。選取不同的特徵對文字分類系統的效能有不同程度的影響。已提出的文字分類特徵選擇方法比較多，常用的方法有：文件頻率(Document Frequency，DF)、資訊增益(Information Gain，IG)、 校驗(CHI)和互資訊(Mutual Information，MI)等方法。另外特徵抽取也是一種特徵降維技術，特徵抽取通過將原始的特徵進行變換運算，形成新的特徵。

常見模型

文件頻率(DF)

  某一片語出現在文件中的頻率稱為文件頻率(DF)。計算形式如式所示：

  基於文件頻率的特徵選擇一般過程：
  1) 設定文件頻率DF的上界閾值∂_u 和下界閾值∂_l；
  2) 統計訓練資料集中片語 的文件頻率 ；
  3) ∀ DF(t_k)< ∂_l：由於片語t_k 在訓練集中出現的頻率過低，不具有代表性，因此從特徵空間中去掉片語t_k；
  4) ∀ DF(t_k)< ∂_u ：由於片語t_k 在訓練集中出現的頻率過高，不具有區分度，因此從特徵空間中去掉片語t_k ；
  所以最終選取的作為特徵的片語必須滿足條件∂_l≤ DF(t_k

)≤ ∂_u ： 。
  基於文件頻率的特徵選擇方法，一方面可以降低特徵向量的複雜度；另一方面還可能提高分類的準確率，因為按此種特徵選擇方法可以刪除一部分噪聲資料。雖然DF方法簡便、易實現，但其理論依據不嚴謹，屬於一種借代演算法。根據資訊理論可知，某些片語雖然出現的頻率低，但是卻含有較多的資訊，對於分類可能更應該重視這些片語。對於這類片語就不應該使用DF特徵選擇方法將其直接從特徵向量排除。

卡方校驗(CHI)

  卡方( χ²)校驗(Chi-Square Test，CHI)是一種數理統計中用來檢驗兩個變數獨立性的方法。其基本思想是通過檢驗實際值與理論值的偏差來確定理論的正確與否。在文字分類的特徵選擇中，用它來衡量類別c_i

與片語t_k 之間關聯度，並假設片語t_k 與類別c_i 之間服從具有一階自由度的χ²分佈。片語對於某類的χ²統計量越高，其與該類之間的關聯度愈大，攜帶的資訊隨之也較多，反之則較少。
  卡方校驗具體做法：
  1) 首先假設兩個變數是獨立的(原假設)；
  2) 然後計算實際測量值(觀察值)與“如果兩者確實獨立”的情況下的理論值的偏差程度；
  3) 若偏差足夠小，就認為誤差屬於自然樣本誤差，是測量方式不精確引起或者屬於偶然現象的，此時就接受原假設，認定二者相互獨立；
  4) 若偏差大到某一程度，使得誤差不太可能是偶然現象或者測量不精確所致，就否定原假設，而接受侯選假設，認定二者不相互獨立，即二者相關。
  假設片語與類關係如表表示：

  其中：
  1) A表示屬於類別c_i 且包含片語t_k 的文件數，
  b) B表示不屬於類別c_i 但包含片語t_k 的文件數，
  c) C表示屬於類別c_i 但不包含片語t_k 的文件數，
  d) D表示既不屬於類別c_i 也不包含片語t_k 的文件數，
  e) 設N表示訓練集中文件總數。
  特徵項t_k 對類c_i 的卡方統計量計算如式:

  由於卡方校驗統計的是出現片語t_k 的文件數，並沒有考慮一篇文件中片語出現的次數，這會使得它偏袒低頻詞。卡方校驗考慮的是範圍數量而不是整體數量。這就是卡方檢驗著名的“低頻詞缺陷”。因此開方檢驗也經常同詞頻等綜合考慮來取長補短。

資訊增益(IG)

  資訊增益(Information Grain，IG)根據片語t_k 為整個分類系統能夠帶來的資訊量來衡量該片語的重要性，從而對該片語的進行選擇取捨。如果片語帶來的資訊越多，該片語就越重要，反之則越不重要。資訊增益是針對一個片語而言，系統包含片語t_k 和排除它的情況下資訊量的差值就是這個片語為系統帶來的資訊量，即增益。其中，資訊量的多少由資訊熵來衡量。因此，資訊增益等於不考慮片語t_k 時文件的資訊熵和考慮該片語後文檔的資訊熵的差值。資訊增益的計算如式:

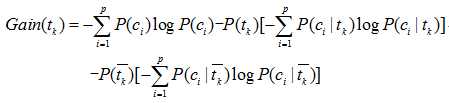
  其中：
  a) P(c_i) 表示類別c_i 在訓練集中出現的概率，
  b) P(t_k) 表示訓練集中包含片語t_k 的概率，
  c) P(c_i|t_k) 表示文字包含片語t_k 時，屬於類別c_i 的條件概率，
  d) P(t_k^–) 表示訓練集中不包含片語t_k 的概率，
  e) P(c_i|t_k^–) 表示文字不包含片語t_k 時，屬於類別c_i 的條件概率。

互資訊(MI)

  互資訊(Mutual Information，MI)也是自然語言處理模型分析的常用方法，它依據資訊理論基礎，來度量兩個變數間的相關性。依據互資訊進行特徵選擇的假設前提：在類別c_i 中出現頻率較高，而在其他類別 !c_i 中出現頻率較低的片語t_k 與類別c_i 的互資訊較大。
  基本思想：互資訊越大，片語t_k 與類別c_i 越可能共同出現。如果A、B、C、D的含義如上表，那麼，片語t_k 與類別c_i 的互資訊計算如式：

如果片語t_k 和類別c_i 無關，則P(t_k,c_i)=P(t_k)XP(c_i)，那麼I(t_k,c_i)=0 。
  由於該特徵選擇方法不需要對片語和類別之間性質作任何假設，因此普遍認為該方法適合於文字分類的特徵選擇。不過互資訊方式的特徵選擇存在“低頻詞強依賴”現象，就是那些訓練集中出現很少的片語，互資訊值很大，很容易被選為特徵。然而這些片語可能是錯誤的單詞或者分詞系統切分錯誤的詞語，在對未標註樣本進行分類或測試的時候，將很難匹配到該片語，這就很容易造成分類的正確度偏低。

參考文獻：
[1] Jain，A.K.，Zongker，D. Feature selection: Evaluation, application, and small sample performance . IEEE Trans. on Pattern Analysis and Machine Intelligence，19(2)：153−158.
[2] Yang，Y. M.，Pedersen，J. O. A comparative study on feature selection in text categorization. In: Proc. of the 14th Int’l Conf. on Machine Learning (ICML’97). 412−420.
[3] Jain，A.K.，Duin，R. P. W.，Mao，J. C. Statistical pattern recognition: A review. IEEE Trans. on Pattern Analysis and Machine Intelligence，22(1)：4−37.
[4] 朱靖波，王會珍，張希娟.面向文字分類的混淆類判別技術.軟體學報，19(3):630-639.