資料結構之圖的遍歷
圖的遍歷是和樹的遍歷類似,我們希望從圖中某一點出發訪問圖中其餘頂點,且使每一個頂點僅被訪問一次,這一過程就叫做圖的遍歷。
深度優先遍歷
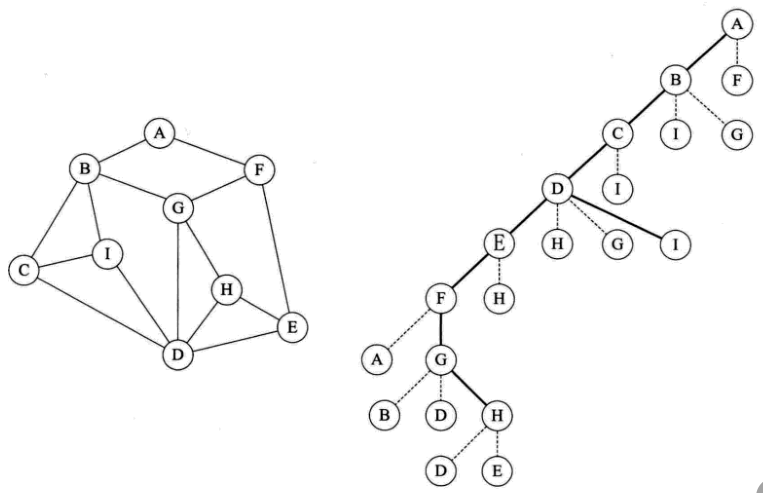
深度優先遍歷,也稱之為深度優先搜尋,簡稱DFS。首先指定一個規則,在沒有碰到重複頂點的情況下,始終向右手邊走,A-B-C-D-E-F,走到F時發現A(已被標記)已經走過了,因此選擇從右數第二條路,到了G-H,此時H周圍的結點都被標記已經走過了。
此時是否已經遍歷了所有的頂點?沒有。所以,我們原路返回,從H回到G,還是無路可走,再返回到F、E、D,到D時發現有個I沒有走過,標記下來,繼續返回,直到回到A完成遍歷任務。可以發現深度優先遍歷是一個遞迴過程
前序遍歷。
- 採用陣列的方式:
鄰接矩陣, 。 - 採用連結串列的方式:
鄰接表, ,適合點多邊少的稀疏圖。
深度優先搜尋遇到如下情況需要中斷當前搜尋並返回上一狀態,俗稱"剪枝":
1. 當前狀態無法在進行狀態遷移時
2. 狀態遷移生成了曾經生成過的狀態時
3. 根據問題性質可斷定搜尋無法找到答案時(無解)
對於有向圖而言,由於它只是對通道存在可行或不可行,演算法上沒有變化,是完全可以通用的。
廣度優先遍歷
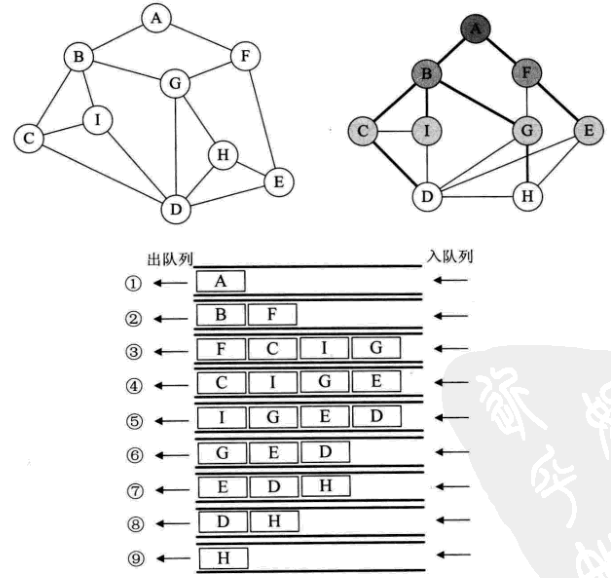
如果說圖的深度優先遍歷類似於樹的前序遍歷,那麼圖的廣度優先遍歷就類似於樹的層序遍歷。可將如下左圖稍微變形,變形原則是頂點A放在最上一層,讓與它有邊的頂點B、F為第二層,再讓與B和F有邊的頂點C、I、G、E為第三層,再將這第四個頂點有邊的D、H放在第四層:
圖的深度和廣度遍歷(鄰接矩陣)
#include "stdio.h"
#include "stdlib.h"
#include "io.h"
#include "math.h"
#include "time.h"
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
typedef int Status; /* Status是函式的型別,其值是函式結果狀態程式碼,如OK等 */
typedef int Boolean; /* Boolean是布林型別,其值是TRUE或FALSE */
typedef char VertexType; /* 頂點型別應由使用者定義 */
typedef int EdgeType; /* 邊上的權值型別應由使用者定義 */
#define MAXSIZE 9 /* 儲存空間初始分配量 */
#define MAXEDGE 15
#define MAXVEX 9
#define INFINITY 65535
typedef struct
{
VertexType vexs[MAXVEX]; /* 頂點表 */
EdgeType arc[MAXVEX][MAXVEX];/* 鄰接矩陣,可看作邊表 */
int numVertexes, numEdges; /* 圖中當前的頂點數和邊數 */
}MGraph;
/* 用到的佇列結構與函式********************************** */
/* 迴圈佇列的順序儲存結構 */
typedef struct
{
int data[MAXSIZE];
int front; /* 頭指標 */
int rear; /* 尾指標,若佇列不空,指向佇列尾元素的下一個位置 */
}Queue;
/* 初始化一個空佇列Q */
Status InitQueue(Queue *Q)
{
Q->front = 0;
Q->rear = 0;
return OK;
}
/* 若佇列Q為空佇列,則返回TRUE,否則返回FALSE */
Status QueueEmpty(Queue Q)
{
if (Q.front == Q.rear) /* 佇列空的標誌 */
return TRUE;
else
return FALSE;
}
/* 若佇列未滿,則插入元素e為Q新的隊尾元素 */
Status EnQueue(Queue *Q, int e)
{
if ((Q->rear + 1) % MAXSIZE == Q->front) /* 佇列滿的判斷 */
return ERROR;
Q->data[Q->rear] = e; /* 將元素e賦值給隊尾 */
Q->rear = (Q->rear + 1) % MAXSIZE;/* rear指標向後移一位置, */
/* 若到最後則轉到陣列頭部 */
return OK;
}
/* 若佇列不空,則刪除Q中隊頭元素,用e返回其值 */
Status DeQueue(Queue *Q, int *e)
{
if (Q->front == Q->rear) /* 佇列空的判斷 */
return ERROR;
*e = Q->data[Q->front]; /* 將隊頭元素賦值給e */
Q->front = (Q->front + 1) % MAXSIZE; /* front指標向後移一位置, */
/* 若到最後則轉到陣列頭部 */
return OK;
}
/* ****************************************************** */
void CreateMGraph(MGraph *G)
{
int i, j;
G->numEdges = 15;
G->numVertexes = 9;
/* 讀入頂點資訊,建立頂點表 */
G->vexs[0] = 'A';
G->vexs[1] = 'B';
G->vexs[2] = 'C';
G->vexs[3] = 'D';
G->vexs[4] = 'E';
G->vexs[5] = 'F';
G->vexs[6] = 'G';
G->vexs[7] = 'H';
G->vexs[8] = 'I';
for (i = 0; i < G->numVertexes; i++)/* 初始化圖 */
{
for (j = 0; j < G->numVertexes; j++)
{
G->arc[i][j] = 0;
}
}
G->arc[0][1] = 1;
G->arc[0][5] = 1;
G->arc[1][2] = 1;
G->arc[1][8] = 1;
G->arc[1][6] = 1;
G->arc[2][3] = 1;
G->arc[2][8] = 1;
G->arc[3][4] = 1;
G->arc[3][7] = 1;
G->arc[3][6] = 1;
G->arc[3][8] = 1;
G->arc[4][5] = 1;
G->arc[4][7] = 1;
G->arc[5][6] = 1;
G->arc[6][7] = 1;
for (i = 0; i < G->numVertexes; i++)
{
for (j = i; j < G->numVertexes; j++)
{
G->arc[j][i] = G->arc[i][j];
}
}
}
Boolean visited[MAXVEX]; /* 訪問標誌的陣列 */
/* 鄰接矩陣的深度優先遞迴演算法 */
void DFS(MGraph G, int i)
{
int j;
visited[i] = TRUE;
printf("%c ", G.vexs[i]);/* 列印頂點,也可以其它操作 */
for (j = 0; j < G.numVertexes; j++)
if (G.arc[i][j] == 1 && !visited[j])
DFS(G, j);/* 對為訪問的鄰接頂點遞迴呼叫 */
}
/* 鄰接矩陣的深度遍歷操作 */
void DFSTraverse(MGraph G)
{
int i;
for (i = 0; i < G.numVertexes; i++)
visited[i] = FALSE; /* 初始所有頂點狀態都是未訪問過狀態 */
for (i = 0; i < G.numVertexes; i++)
if (!visited[i]) /* 對未訪問過的頂點呼叫DFS,若是連通圖,只會執行一次 */
DFS(G, i);
}
/* 鄰接矩陣的廣度遍歷演算法 */
void BFSTraverse(MGraph G)
{
int i, j;
Queue Q;
for (i = 0; i < G.numVertexes; i++)
visited[i] = FALSE;
InitQueue(&Q); /* 初始化一輔助用的佇列 */
for (i = 0; i < G.numVertexes; i++) /* 對每一個頂點做迴圈 */
{
if (!visited[i]) /* 若是未訪問過就處理 */
{
visited[i] = TRUE; /* 設定當前頂點訪問過 */
printf("%c ", G.vexs[i]);/* 列印頂點,也可以其它操作 */
EnQueue(&Q, i); /* 將此頂點入佇列 */
while (!QueueEmpty(Q)) /* 若當前佇列不為空 */
{
DeQueue(&Q, &i); /* 將隊對元素出佇列,賦值給i */
for (j = 0; j<G.numVertexes; j++)
{
/* 判斷其它頂點若與當前頂點存在邊且未訪問過 */
if (G.arc[i][j] == 1 && !visited[j])
{
visited[j] = TRUE; /* 將找到的此頂點標記為已訪問 */
printf("%c ", G.vexs[j]); /* 列印頂點 */
EnQueue(&Q, j); /* 將找到的此頂點入佇列 */
}
}
}
}
}
}
int main(void)
{
MGraph G;
CreateMGraph(&G);
printf("\n深度遍歷:");
DFSTraverse(G);
printf("\n廣度遍歷:");
BFSTraverse(G);
system("pause");
return 0;
}
執行結果:
深度遍歷:A B C D E F G H I
廣度遍歷:A B F C G I E D H
圖的深度和廣度遍歷(鄰接表)
#include "stdio.h"
#include "stdlib.h"
#include "io.h"
#include "math.h"
#include "time.h"
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 9 /* 儲存空間初始分配量 */
#define MAXEDGE 15
#define MAXVEX 9
#define INFINITY 65535
typedef int Status; /* Status是函式的型別,其值是函式結果狀態程式碼,如OK等 */
typedef int Boolean; /* Boolean是布林型別,其值是TRUE或FALSE */
typedef char VertexType; /* 頂點型別應由使用者定義 */
typedef int EdgeType; /* 邊上的權值型別應由使用者定義 */
/* 鄰接矩陣結構 */
typedef struct
{
VertexType vexs[MAXVEX]; /* 頂點表 */
EdgeType arc[MAXVEX][MAXVEX];/* 鄰接矩陣,可看作邊表 */
int numVertexes, numEdges; /* 圖中當前的頂點數和邊數 */
}MGraph;
/* 鄰接表結構****************** */
typedef struct EdgeNode /* 邊表結點 */
{
int adjvex; /* 鄰接點域,儲存該頂點對應的下標 */
int weight; /* 用於儲存權值,對於非網圖可以不需要 */
struct EdgeNode *next; /* 鏈域,指向下一個鄰接點 */
}EdgeNode;
typedef struct VertexNode /* 頂點表結點 */
{
int in; /* 頂點入度 */
char data; /* 頂點域,儲存頂點資訊 */
EdgeNode *firstedge;/* 邊表頭指標 */
}VertexNode, AdjList[MAXVEX];
typedef struct
{
AdjList adjList;
int numVertexes, numEdges; /* 圖中當前頂點數和邊數 */
}graphAdjList, *GraphAdjList;
/* **************************** */
/* 用到的佇列結構與函式********************************** */
/* 迴圈佇列的順序儲存結構 */
typedef struct
{
int data[MAXSIZE];
int front; /* 頭指標 */
int rear; /* 尾指標,若佇列不空,指向佇列尾元素的下一個位置 */
}Queue;
/* 初始化一個空佇列Q */
Status InitQueue(Queue *Q)
{
Q->front = 0;
Q->rear = 0;
return OK;
}
/* 若佇列Q為空佇列,則返回TRUE,否則返回FALSE */
Status QueueEmpty(Queue Q)
{
if (Q.front == Q.rear) /* 佇列空的標誌 */
return TRUE;
else
return FALSE;
}
/* 若佇列未滿,則插入元素e為Q新的隊尾元素 */
Status EnQueue(Queue *Q, int e)
{
if ((Q->rear + 1) % MAXSIZE == Q->front) /* 佇列滿的判斷 */
return ERROR;
Q->data[Q->rear] = e; /* 將元素e賦值給隊尾 */
Q->rear = (Q->rear + 1) % MAXSIZE;/* rear指標向後移一位置, */
/* 若到最後則轉到陣列頭部 */
return OK;
}
/* 若佇列不空,則刪除Q中隊頭元素,用e返回其值 */
Status DeQueue(Queue *Q, int *e)
{
if (Q->front == Q->rear) /* 佇列空的判斷 */
return ERROR;
*e = Q->data[Q->front]; /* 將隊頭元素賦值給e */
Q->front = (Q->front + 1) % MAXSIZE; /* front指標向後移一位置, */
/* 若到最後則轉到陣列頭部 */
return OK;
}
/* ****************************************************** */
void CreateMGraph(MGraph *G)
{
int i, j;
G->numEdges = 15;
G->numVertexes = 9;
/* 讀入頂點資訊,建立頂點表 */
G->vexs[0] = 'A';
G->vexs[1] = 'B';
G->vexs[2] = 'C';
G->vexs[3] = 'D';
G->vexs[4] = 'E';
G->vexs[5] = 'F';
G->vexs[6] = 'G';
G->vexs[7] = 'H';
G->vexs[8] = 'I';
for (i = 0; i < G->numVertexes; i++)/* 初始化圖 */
{
for (j = 0; j < G->numVertexes; j++)
{
G->arc[i][j] = 0;
}
}
G->arc[0][1] = 1;
G->arc[0][5] = 1;
G->arc[1][2] = 1;
G->arc[1][8] = 1;
G->arc[1][6] = 1;
G->arc[2][3] = 1;
G->arc[2][8] = 1;
G->arc[3][4] = 1;
G->arc[3][7] = 1;
G->arc[3][6] = 1;
G->arc[3][8] = 1;
G->arc[4][5] = 1;
G->arc[4][7] = 1;
G->arc[5][6] = 1;
G->arc[6][7] = 1;
for (i = 0; i < G->numVertexes; i++)
{
for (j = i; j < G->numVertexes; j++)
{
G->arc[j][i] = G->arc[i][j];
}
}
}
/* 利用鄰接矩陣構建鄰接表 */
void CreateALGraph(MGraph G, GraphAdjList *GL)
{
int i, j;
EdgeNode *e;
*GL = (GraphAdjList)malloc(sizeof(graphAdjList));
(*GL)->numVertexes = G.numVertexes
相關推薦
資料結構之圖的遍歷
圖的遍歷是和樹的遍歷類似,我們希望從圖中某一點出發訪問圖中其餘頂點,且使每一個頂點僅被訪問一次,這一過程就叫做圖的遍歷。
深度優先遍歷
深度優先遍歷,也稱之為深度優先搜尋,簡稱DFS。首先指定一個規則,在沒有碰到重複頂點的情況下,始終向右手邊走,A-B-C-D-E-F,走到F時發
資料結構之圖篇(2):圖的基本操作 深度和廣度遍歷
程式碼實現
main.cpp(主函式)
#include <iostream>
#include "CMap.h"
using namespace std;
/**
圖的的儲存:鄰接矩陣
圖的遍歷:深度+廣度
A
/ \
資料結構之圖的深度優先遍歷和廣度優先遍歷
1.圖的簡單介紹
上圖就是一個圖(無線圖),由頂點和連線組成
圖可以分為無向圖和有向圖(這個又有出度、入度的概念)、網,一般來說圖有兩種常用的表示方式,鄰接矩陣(用二維陣列的形式表示)和鄰接表(主要是陣列+連結串列的形式表示),圖常用的遍歷方式有深度優先遍歷(DFS)和廣
資料結構之圖的遍歷和部分性質
無向圖和有向圖
1、無向圖中,任意兩個頂點之間都存在邊的話,就是無向完全圖。
含有n個頂點的無向完全圖有n×(n−1)2條邊。
有向圖中,若任意兩個頂點之間都存在方向互為相反的有向邊,則就是有向完全圖。
含有n個頂點的有向完全圖有n×(
資料結構之圖(鄰接表儲存,DFS和BFS遍歷)
來看下面的一個簡單的圖,
那麼這樣的一個圖,我們應該用什麼儲存結構來儲存它呢?常用的是鄰接矩陣和鄰接表,這裡鄰接矩陣不做講解,如下所有程式碼都是以鄰接表作為儲存結構,所以這裡就只講解下鄰接表。那麼什麼是鄰接表呢?如何構造呢?
鄰接表是一
嚴蔚敏-資料結構-樹的遍歷
前序非遞迴遍歷
PreOrderTraverse(BiTree T)
{
InitStack(S);
p=T;
while (p||!StackEmpty)
{
if(p)
{
print(p);
if(p->rchild)
{
資料結構之圖的關鍵路徑
title: 資料結構之圖的關鍵路徑 tags: 資料結構與演算法之美
一、AOE和AOV網
1.AOE網
AOE-網:指用邊表示活動的網,是一個帶權的有向無環圖,其中,頂點表示事件弧表示活動,權表示活動持續的時間,通常一個AOE-網可用來估算工程的完成時間。
2.AOV網
指用頂點表示活動
資料結構之圖(帶權圖 迪傑斯特拉演算法)
// 主要思想是: 每次尋找最小的邊 這樣的話從上一個節點 到這個節點的值 是最小的 當找到最小的邊時,把final[v] = true 表示從原點到這個節點的最小值 已經找到了
<!DOCTYPE html> <html> &l
資料結構之圖(鄰接表 稀疏圖)
<!DOCTYPE html> <html> <head> <title>鄰接表</title> <meta charset="utf-8">
資料結構之圖的最小生成樹
我們把構造連通網的最小代價生成樹稱為最小生成樹,找連通網的最小生成樹,經典的有兩種演算法:普里姆演算法(Prim)和克魯斯卡爾演算法(Kruskal)。
普里姆演算法
有如下鄰接矩陣,9個頂點,左側數字為行號,INFINITY為極大值65535,MAXVEX為頂點個數最大值,此處
資料結構之圖篇(1):概述
圖的概念
1.有向圖(由節點和方向箭頭構成)無向圖(只有節點,相當於每條連線都是雙向的) 2.出度:頂點的箭頭指出;入度:頂點的箭頭指入; 3.有向圖:弧;無向圖:邊; 5.權值:弧或者邊上的資料
圖的儲存結構
陣列儲存
1.鄰接矩陣(頂點陣列【索引+資料】+鄰接矩
資料結構 - 樹的遍歷方法舉例
樹的遍歷
我們已經見到了樹資料結構的基本功能,現在是看樹的一些額外使用模式的時候了。這些使用模式可以分為我們訪問樹節點的三種方式。有三種常用的模式來訪問樹中的所有節點。這些模式之間的差異是每個節點被訪問的順序。我們稱這種訪問節點方式為“遍歷”。我們將看到三種遍歷方式稱為前序,中序和後序
資料結構之圖學習筆記
一、圖的定義:
圖(Graph)是由頂點的有窮非空集合和頂點之間邊的集合組成,通常表示為:G(V,E),其中,G表示一個圖,V表示圖G中頂點的集合,E是圖G中的邊集合。
a.線性表中的資料元素我們稱為元素,樹中資料元素稱為節點,而圖中的
資料結構之圖論之鄰接表
還是插入一段程式碼來解釋鄰接表的建立過程。
//自己建立一個鄰接表
//邊表結點
typedef struct {
int adjvex;//該邊的頭結點
int weight;//權值
EdgeNode *next;//該邊尾結點的下一條邊
}EdgeNo
資料結構之圖論之深度搜索之八皇后
//八皇后問題
#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<cmath>
using namespace std;
int a[100],coun
資料結構之圖
1.圖的定義
圖(graph)是由一些點(vertex)和這些點之間的連線(edge)所組成的;其中,點通常稱為頂點(vertex),而點到點之間的連線通常稱之為邊或者弧(edge)。通常記為G=(V,E)。
2.圖的分類
圖通常分為有向圖和無向圖,而其表示表示方式
資料結構知識整理 - 遍歷二叉樹的應用
主要內容
建立二叉連結串列
複製二叉樹
計算二叉樹深度
統計二叉樹的結點個數
建立二叉連結串列
在先序遍歷的遞迴演算法中,將輸出語句改為輸入語句即可。(可回顧“遞迴演算法”)
需要注意的是,遞迴演算法會遍歷滿二叉樹中的每一個結點,
資料結構之圖(圖的基本操作)
由於圖的基本操作的程式碼較多,我放到這一章來寫。圖可以用兩種方法來儲存,但是本人偏愛連結串列的表示方法,所以以下程式碼也都是是基於鄰接連結串列的儲存方式。
1 /*
2 以下儲存結構參考嚴蔚敏版資料結構,不懂的可以翻閱檢視
3 */
4 const int UNDIGR
資料結構之圖(圖的簡介)
圖的定義:
一個圖G = (V,E)由頂點(vertex)集 V 合邊(edge)集 E 組成。每條邊(v,w)就是一個點對,其中v,w ∈ V。有時也把邊稱作弧。如果點對是有序的,那麼圖就叫做有向圖。頂點 v 和 w 領接邊 (v,w) ∈ E。在一個具有邊(
資料結構-----後序遍歷二叉樹非遞迴演算法(利用堆疊實現)
一、非遞迴後序遍歷演算法思想
後序遍歷的非遞迴演算法中節點的進棧次數是兩個,即每個節點都要進棧兩次,第二次退棧的時候才訪問節點。
第一次進棧時,在遍歷左子樹的過程中將"根"節點進棧,待左子樹訪問完後,回溯的節點退棧,即退出這個"根"節點,但不能立即訪問,只能藉助於這個"根"