資料結構之圖
1.圖的定義
圖(graph)是由一些點(vertex)和這些點之間的連線(edge)所組成的;其中,點通常稱為頂點(vertex),而點到點之間的連線通常稱之為邊或者弧(edge)。通常記為G=(V,E)。
2.圖的分類
圖通常分為有向圖和無向圖,而其表示表示方式分為鄰接矩陣和鄰接連結串列。具體表示如下圖。

對於無向圖,其所有的邊都不區分方向。G=(V,E)。其中,
<1>V={1,2,3,4,5}。V表示有”1,2,3,4,5”幾個頂點組成的集合。
<2>E={(1,2),(1,5),(2,1),(2,5),(2,4),(2,3),(3,2),(3,4),(4,3),(4,2),(4,5),(5,1),(5,2),(5,4)}。E就是表示所有邊組成的集合,如(1,2)表示由頂點1到頂點2連線成的邊。

對於有向圖,其所有的邊都是有方向的。G=(V,E)。其中,
<1>V={1,2,3,4,5}。V表示有”1,2,3,4,5”幾個頂點組成的集合。
<2>E={<1,2>,<2,5><5,4>,<4,2><3,5>,<3,6>,<6,6>}。E就是表示所有邊組成的集合,如<1,2>表示由頂點1到頂點2連線成的邊。注意又有向圖邊和無向圖邊表示方法的不同,有向圖的邊是向量,而無向圖只是普通的括號。
針對鄰接矩陣和鄰接連結串列兩種不同的表示方式,有如下優缺點:
<1>鄰接矩陣由於沒有相連的邊也佔據空間,相對於鄰接連結串列,存在空間浪費的問題;
<2>但是在查詢的時候,鄰接連結串列會比較耗時,對於鄰接矩陣來說,它的查詢複雜度就是O(1)。
用鄰接表表示圖的程式碼
#define MAX 100 typedef struct ENode //鄰接表中表對應的連結串列的頂點 { int ivex; //該邊所指向的頂點的位置 int weight; //該邊的權值 struct ENode *next_edge; //指向下一條邊的指標 }ENode,*PENode; typedef struct VNode //鄰接表中表的頂點 { char data; //頂點的資料 struct VNode *first_edge; //指向第一條依附該頂點的邊 }VNode; typedef struct LGraph //鄰接表 { int vexnum; //圖的頂點數 int edgenum; //圖的邊數 VNode vexs[MAX]; }LGraph;
- 3.度、權、連通圖等概念
對於無向圖來說,它的頂點的度就是指關聯於該頂點的邊的數目;而對於有向圖來說,分為入度和出度,所謂入度就是進入該頂點邊的數目,出度就是離開這個頂點邊的數目,有向圖的度就是入度加出度。
如下圖有向圖(a)所示,對於頂點3,它的入度為2,出度為1,度為3。

圖還被分為有權圖和無權圖,所謂有權圖就是每條邊都具有一定的權重,通常就是邊上的那個數字;而無權圖就是每條邊沒有權重,也可以理解為權重為。如下圖所示即為有權圖,(A,B)的權就是13。
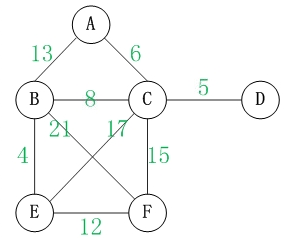
如果一個無向圖中每個頂點從所有其他頂點都是可達的,則稱該圖是連通的;如果一個有向圖中任意兩個頂點互相可達,則該有向圖是強連通的。
如圖(b)中有3個連通分量:{1,2,5},{3,6},{4}。若一個無向圖只有一個連通分量,則該無向圖連通。
而圖(a)中有3個強連通分量:{1,2,4,5},{3},{6}。{1,2,4,5}中所有頂點對互相可達。而頂點2與6不能相互可達,所以不能構成一個強連通分量。

4.深度優先搜尋(Depth First Search,DFS)
圖的深度優先演算法有點類似於樹的前序遍歷,首先圖中的頂點均未被訪問,確定某一頂點,從該頂點出發,依次訪問未被訪問的鄰接點,直到某個鄰接點沒有未被訪問鄰接點時,則回溯父節點(此處我們將先被訪問的節點當做後被訪問節點的父節點,例如對於節點A、B,訪問順序是A ->B,則稱A為B的父節點),找到父節點未被訪問的子節點;如此類推,直到所有的頂點都被訪問到。
注意,深度優先的儲存方式一般是以棧的方式儲存。
<1>無向圖的深度優先搜尋

<2>有向圖的深度優先搜尋

<3>深度優先搜尋程式碼
static void DFS(LGraph G, int i,int *visited)
{
Enode *node;E
printf(“%c”,G.vexs[i].data);
node = G.vexs[i].first_edge;
while(node != NULL)
{
if(!visited[node->ivex])
DFS(G, node->ivex, visited); //遞迴呼叫DFS
node = node->next_edge;
}
}- 5.廣度優先搜尋(Breadth First Search,BFS)
從圖中的某個頂點出發,訪問它所有的未被訪問鄰接點,然後分別從這些鄰接點出發訪問它的鄰接點。說白了就是一層一層的訪問,“淺嘗輒止”!
注意,廣度優先搜尋的儲存方式一般是以佇列的方式儲存。
<1>無向圖的廣度優先搜尋

<2>有向圖的廣度優先搜尋

<3>廣度優先搜尋程式碼
void BFS(LGraph G)
{
int head = 0;
int rear = 0;
int queue[MAX]; //輔助佇列
int visited[MAX]; //頂點訪問標記
eNode *node;
for(int i = 0; i < G.vexnum; i++)
visited[i] = 0; //初始化所有頂點,標記為未訪問
printf(“BFS:”);
for(int i = 0; i < G.vexnum; i++)
{
if(!visited[i])
{
visited[i] = 1;
printf(“%c”,G.vexs[i].data);
queue[rear++] = i; //入隊
}
while(head != rear)
{
int j = queue[head++]; //出隊
node = G.vexs[j].first_edge;
while(node != NULL)
{
int k = node->ivex;
if(!visited[k])
{
visited[k] = 1;
printf(“%c”,G.vesx[k].data);
queue[rear++] = k;
}
node = node->next_edge;
}
}
}
printf(“\n”);
}- 6.拓撲排序
拓撲排序(Topological Order)是指講一個有向無環圖(Directed Acyclic Graph,DAG)進行排序而得到一個有序的線性序列。
取個栗子,例如我們早上起床的穿衣順序,如下圖所示。穿衣的順序也是有個優先順序的,有些衣服就必須優先穿上,例如領帶依賴於襯衣,所以領帶最終排在襯衣之後;對圖a中的元素進行合理的排序,就得到了圖b的次序圖。注意,該次序圖不是唯一的。


int topological_sort(LGraph G)
{
int num = G.vexnum;
ENode *node;
int head = 0; //輔助佇列的頭
int rear = 0; // 輔助佇列的尾
int *ins = (int *)malloc(num * sizeof(int)); //入度陣列
char *tops = (char *)malloc(num * sizeof(char)); //拓撲排序結果陣列,記錄每個節點排序後的序號
int *queue = (int *)malloc(num * sizeof(int)); //輔助佇列
assert(ins != NULL && tops != NULL && queue != NULL)
memset(ins, 0, num * sizeof(int));
memset(tops, 0, num * sizeof(char));
memset(queue, 0, num * sizeof(int));
for(int i = 0; i < num; i ++) //統計每個頂點的入度數
{
node = G.vexs[i].first_edge;
while(node != NULL)
{
ins[node->ivex]++;
node = node->next_edge;
}
}
for(int i = 0; i < num; i++) //將所有入度為0的頂點裝入佇列
if(ins[i] == 0)
queue[rear++] = i;
while(head != rear) //佇列非空
{
int j = queue[head++]; //出佇列,j為頂點的序號
tops[index++] = G.vexs[j].data; //將該頂點新增到tops中,tops是排序結果
node = G.vexs[j].first_edge; //獲取以該頂點為起點的出邊佇列
while(node != NULL)
{
ins[node->ivex]--; //將節點node關聯的節點的入度減1
if(ins[node->ivex] == 0) //若節點的入度為0,則將其新增到佇列中
queue[rear++] = node->ivex;
node = node->next_edge;
}
}
if(index != G.vexnum)
{
printf(“Graph has a cycle!\n”);
free(queue);
free(ins);
free(tops);
return 1; //1表示失敗,該有向圖是有環的
}
printf(“== TopSort: ”); //列印拓撲排序結果
for(int i = 0; i < num; i++)
printf(“%c”,top[i]);
printf(“\n”);
free(queue);
free(ins);
free(tops);
return 0;
}- 7.最小生成樹
所謂最小生成樹就是將圖中的頂點全部連線起來,此時這個邊的權重最小,並且連線起來的是一個無環的樹。很容易知道,若此時的頂點是n,則邊的數量為n-1。所以在一個圖中找最小生成樹就是找最小權值的邊,讓這些邊連成一棵樹。常用的演算法有Prim演算法和Kruskal演算法。
<1>Prim演算法
該演算法就是每次迭代選擇權值最小的邊對應的點,加入到最小生成樹中。具體實現如下所示。

第一步:選取頂點A,此時U={A},V-U={B,C,D,E,F,G}。

第二步:選取與A點連線的權值最小的邊,此時就會選擇到B,U={A,B},V-U={C,D,E,F,G}。

以上面的步驟類推,得到如上圖所示的結果,此時U={A,B,C,D,E,F},V-U={G}。注意到C是此次加入的點,而G沒有加入,此時G點的邊應該如何選擇?

最終,得到如圖所示的最小生成樹,此時U={A,B,C,D,E,F,G},V-U={}。
實現程式碼如下:
#define INF (~(0x1<<31)) //最大值(即0X7FFFFFFF)
//返回ch在鄰接表中的位置
static int get_position(LGraph G, char ch)
{
for(int i = 0; i < G.vexnum; i++)
if(G.vexnum[i].data == ch)
return i;
return -1;
}
//獲取G中邊<start,end>的權值;若start到end不連通,則返回無窮大
int getWeight(LGraph G, int start, int end)
{
ENode *node;
if(start == end)
return 0;
node = G.vexs[start].first_edge;
while(node != NULL)
{
if(end == node->ivex)
return node->weight;
node = node->next_edge;
}
return INF;
}
void Prim(LGraph G,int start) //從圖中的第start個元素開始,生成最小樹
{
int index = 0; //prim最小樹的索引,即prims陣列的索引
char prims[MAX]; //prim最小樹的結果陣列
int wights[MAX]; //頂點間邊的權重
//prim最小生成樹中第一個數,即圖中的第start個數
prims[index++] = G.vexs[start].data;
for(int i = 0; i < G.vexnum; i++) //初始化頂點的權值陣列
weights[i] = getWeight(G, start, i); //將每個頂點的權值初始化為“第start個頂點”到“該頂點”的權值
for(int i = 0; i < G.vexnum; i++)
{
if(start == i) //由於從start開始,因此不需要再對第start個頂點進行處理
continue;
int j = 0;
int k = 0;
int min = INF;
//在未被加入到最小生成樹的頂點中,找出權值最小的頂點
while(j < G.vexnum)
{
//若weights[j]=0,則說明該節點已經加入了最小生成樹
if(weights[j] != 0 && weights[j] < min)
{
min = weights[j];
k = j;
}
j++;
}
//經過上面的處理後,在未被加入到最小生成樹的頂點中,權值最小的頂點是第k個頂點。
//將第k個頂點加入最小生成樹的結果陣列中
prims[index++] = G.cexs[k].data;
//將第k個頂點的權值標記為0,表示該頂點已經加入了最小生成樹
weights[k] = 0;
//當第k個頂點被加入到最小生成樹的結果陣列後,更新其他頂點的權值
for(int j = 0; j < G.vexnum; j++)
{
//獲取第k個頂點到第j個頂點的權值
int temp = getWeight(G, k, j);
//當第j個節點沒有被處理,並且需要更新的時候才會更新
if(weights[j] != 0 && temp < weights[j])
weights[j] = temp;
}
}
//計算最小生成樹的權值
int sum = 0;
for(int i = 0; i < index; i++)
{
min = INF;
//獲取prims[i]在G中的位置
int n = get_position(G, prims[i]);
//在vexs[0...i]中,找出到j的權值最小的頂點。
for(int j = 0; j < i; j++)
{
int m = get_position(G,prims[j]);
int temp = getWeight(G, m, n);
if(temp < min)
min = temp;
}
sum += min;
}
//列印最小生成樹
printf(“Prim(%c) = %d : ”, G.vexs[start].data, sum);
for(int i = 0; i < index; i++)
printf(“%c ”,prim[i]);
printf(“\n”);
}<2>Kruskal演算法
該演算法的核心就是對權值進行排序,然後從最小的權值開始,不斷增大權值,如何該權值的所在邊的兩個頂點沒有存在的路徑連在一起,則加入這條邊,否則,則捨棄這條邊,知道所有的點都在這顆樹中。
如下所示的一個圖,我們從中找出最小生成樹。

對於左邊所示的的圖,對各個邊的權值排序之後,我們最先找到權值最小的邊,即AD。然後我們發現還有一個CE,於是CE也會被標記起來。

對於左邊所示的的圖,對各個邊的權值排序之後,我們最先找到權值最小的邊,即AD。然後我們發現還有一個CE,於是CE也會被標記起來。
程式碼如下:
typedef struct edata //邊的結構體
{
char start; //邊的起點
char end; //邊的終點
int weight; //邊的權重
}EData;
EData *get_edges(LGraph G)
{
int index = 0;
ENode *node;
EData *edges;
edges = (EData *)malloc(G.edgnum * sizeof(EData));
for(int i = 0; i < G.vexnum; i++)
{
node = G.vexs[i].first_edge;
while(node != NULL)
{
if(node->ivex > i)
{
edges[index].start = G.vexs[i].data;
edges[index].end = G.vexs[node->ivex].data;
edges[index].weight = node->weight;
index++;
}
node = node->next_edge;
}
}
return edges;
}
void Kruskal(LGraph G)
{
int index = 0; //rets陣列的索引
int vends[MAX] = {0}; //用於儲存“已有最小生成樹”中每個頂點在該最小樹中的終點
EData rets[MAX]; //結果陣列,儲存kruskal最小生成樹的邊
EData *edges; //圖對應的所有邊
edges = get_edges(G); //獲取圖中所有的邊
Sorted_edges(edges, G.edgenum); //對邊按照權值進行排序
for(int i = 0; i < G.edgenum; i++)
{
int numOfStart = get_position(G, edges[i].start); //獲取第i條邊的起點的序號
int numOfEnd = get_position(G, edges[i].end); //獲取第i條邊的終點的序號
int m = get_end(vends, numOfStart); //獲取numOfStart在“已有的最小生成樹”中的終點
int n = get_end(vends, numOfEnd); //獲取numOfEnd在“已有的最小生成樹”中的終點
//如果m!=n,表示邊i與已經新增到最小生成樹中的頂點沒有形成環路
if(m != n)
{
vends[m] = n; //設定m在已有的最小生成樹中的終點為n
rets[index++] = edges[i]; //儲存結果
}
}
free(edges);
//統計並列印最小生成樹的資訊
int length = 0;
for(int i = 0; i < index; i++)
length += rets[i].weight;
printf(“Kruskal = %d : ”,length);
for(int i = 0; i < index; i++)
printf(“(%c,%c)”, rets[i].start, rets[i].end);
printf(“\n”);
}參考文件
《演算法導論》
