How Many Answers Are Wrong

TT and FF are ... friends. Uh... very very good friends -________-b 

FF is a bad boy, he is always wooing TT to play the following game with him. This is a very humdrum game. To begin with, TT should write down a sequence of integers-_-!!(bored). 

Then, FF can choose a continuous subsequence from it(for example the subsequence from the third to the fifth integer inclusively). After that, FF will ask TT what the sum of the subsequence he chose is. The next, TT will answer FF's question. Then, FF can redo this process. In the end, FF must work out the entire sequence of integers. 

Boring~~Boring~~a very very boring game!!! TT doesn't want to play with FF at all. To punish FF, she often tells FF the wrong answers on purpose. 

The bad boy is not a fool man. FF detects some answers are incompatible. Of course, these contradictions make it difficult to calculate the sequence. 

However, TT is a nice and lovely girl. She doesn't have the heart to be hard on FF. To save time, she guarantees that the answers are all right if there is no logical mistakes indeed. 

What's more, if FF finds an answer to be wrong, he will ignore it when judging next answers. 

But there will be so many questions that poor FF can't make sure whether the current answer is right or wrong in a moment. So he decides to write a program to help him with this matter. The program will receive a series of questions from FF together with the answers FF has received from TT. The aim of this program is to find how many answers are wrong. Only by ignoring the wrong answers can FF work out the entire sequence of integers. Poor FF has no time to do this job. And now he is asking for your help~(Why asking trouble for himself~~Bad boy) 

Input

Line 1: Two integers, N and M (1 <= N <= 200000, 1 <= M <= 40000). Means TT wrote N integers and FF asked her M questions. 

Line 2..M+1: Line i+1 contains three integer: Ai, Bi and Si. Means TT answered FF that the sum from Ai to Bi is Si. It's guaranteed that 0 < Ai <= Bi <= N. 

You can assume that any sum of subsequence is fit in 32-bit integer. 

Output

A single line with a integer denotes how many answers are wrong.

Sample Input

10 5
1 10 100
7 10 28
1 3 32
4 6 41
6 6 1

Sample Output

1

題意：求在有n個數中，有m次詢問，每次詢問在這給定的區間和這區間裡數的和為s，求每次給出的是不是正確的和s。也就是和前面的矛盾不矛盾。

分析：要求這些話中是否存在矛盾的問題，很明顯的並查集（在這裡要說一下並查集是什麼：並查集，在一些有N個元素的集合應用問題中，我們通常是在開始時讓每個元素構成一個單元素的集合，然後按一定順序將屬於同一組的元素所在的集合合併，其間要反覆查詢一個元素在哪個集合中。）；首先知道並查集是將具有同一種屬性的元素放在同一棵樹中，然後這一棵樹通過路徑壓縮的方式使其子節點都具有同一個根節點，即指向同一個根節點

但是！！如果如果只是將兩個點進行合併的話肯定是不符合題意，因為這兩點還有一定的關係資訊；這就是帶權並查集的特點

處理帶權並查集的最重要的思想就是用到向量的關係來處理；PS一位神犇blog：https://blog.csdn.net/niushuai666/article/details/6981689

處理的核心思想已經有了，剩下的就是處理相對關係了，也就是細節，先上程式碼

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<queue>
using namespace std;
typedef long long ll;
#define rep(i,a,b) for(int i=a;i<=b;i++)
const int N=1e6+7;
int m,n;
int f[N];
int ran[N];//ran[i]代表i節點到父結點的關係，其實通過f的路徑壓縮就變成到根節點的關係了
int ans=0;
int Findf(int v){
    if(f[v]==v) return v;
    int t=f[v];
    f[v]=Findf(f[v]);
    ran[v]+=ran[t];//……1
    return f[v];
}
void Union(int a,int b,int w){
    int t1=Findf(a);//建立樹的時候將a作為根
    int t2=Findf(b);
    if(t1==t2){//w是b-->a的關係
        if(ran[a]+w!=ran[b])//也是由向量的三角形法則得到的相對關係……2
            ans++;
    }else{

        f[t2]=t1;
        ran[t2]=w+ran[a]-ran[b];//……3
    }
    return;
}
void Init(){
    memset(ran,0,sizeof ran);
    rep(i,0,n+1) f[i]=i;
}
int main()
{
    #ifndef ONLINE_JUDGE
    freopen("in.txt","r",stdin);
    #endif // ONLINE_JUDGE
    while(scanf("%d%d",&n,&m)!=EOF){//不多組輸入就會WA
    ans=0;
    Init();
    rep(i,1,m){int u,v,w;
        scanf("%d%d%d",&u,&v,&w);
        Union(u,v+1,w);//這一點就是一定是u-1,v;或者是u,v+1,這樣才能做到兩者相連線
    }                  //比如，連線區間1--2，3--4，這樣就能將區間1--4連線起來；
    printf("%d\n",ans);
    }
 return 0;
}

在這裡我解釋一下我程式碼標註1 2 3的三行

第一處，也就是標1的那一行（下面就用數字代替行了）：為什麼是"+";首先要明確，ran陣列存放的是下標i到其父節點的關係，那麼既然是關係，由大神的向量的思想就可以知道了為什麼是加，有圖有真相：

假設f[a]=b(f陣列是存放其父節點是誰),由並查集的路徑壓縮的思想，f[a]最終是指向root的，也就是f[a]=root，既然是這樣，那就必須要改變ran[a]的值了，不改變之前ran[a]是存放a到b點的關係，改變之後那就需要存放a到root節點的關係，由向量的三角形的法則，a-->root的關係就是a-->b的關係+b-->root的關係，這就是為什麼相加的原因；

第二處：要知道如果到達當前語句是說明了，a b兩個點的根節點是否相同（其實上面的if語句可以改為if(f[a]==f[b])，也是可以），既然相同那就需要比較了

比如先說了連個區間

1-10 10

1-5 2

6-10 5

跟明顯第三句話就可以看出來問題了，第二個加第三個跟第一個不相等，但是他們表述的區間都是相同的，所以產生矛盾，不過這種矛盾應該怎麼判斷呢，我們可以以它的端點為點建立一個集合，他們的根就是能到達的最左端，如果都有相同的最左端那麼就可以判斷一下是否有矛盾產生。

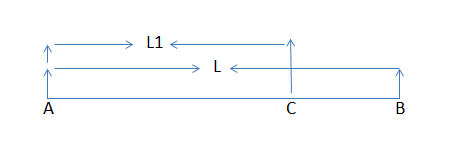
比如上面這個圖, 我們已經知道了AB的長度和AC的長度，如果下面再來一個CB，我們就可以知道C的最左端是A，B的最左端也是A，那麼就可以判斷一個AC+CB的長度是不是等於AB的長度就可以了。。。。
借用原文：https://blog.csdn.net/yu121380/article/details/80453611 

其實本質上還是向量相加原則

第三處：在處理壓縮並查集的時候子節點雖然在函式遞迴的過程中相會連線，但是如果說兩者存在關心那就需要將兩者的根節點相連，在這裡我採用的是將其“靠左原則”，什麼意思？

就是看上面的Union函式傳參a不是在b的左邊嗎，如果將其兩者的的根節點合併，那麼就是f[rootb]=roota，這就是b的根節點就是a的根節點的孩子了；當然你也可以換過來；

同樣的ran的關係陣列也要做同樣的處理，這裡的處理還是靠左原則，

（這個圖和我的靠左原則正好反了，這是靠右，注意一下將roota-->rootb改為rootb-->roota,a-->b改為b-->a,最好自己再重新畫一下）借用這張圖就能說明是怎麼相加的：

我要將roota連線到rootb上，就是ran[roota]等於什麼；

我們呢現在有a-->b的關係w,b-->rootb的關係ran[b]，a-->roota的關係ran[a]，由向量的加法就能得到rootb-->roota=ran[a]+w-ran[b];

PS：poj1182也是帶權並查集，其處理的細節有點不同，需要推出他們的關係來