How Many Answers Are Wrong HDU - 3038

TT and FF are ... friends. Uh... very very good friends -________-b 

FF is a bad boy, he is always wooing TT to play the following game with him. This is a very humdrum game. To begin with, TT should write down a sequence of integers-_-!!(bored). 

Then, FF can choose a continuous subsequence from it(for example the subsequence from the third to the fifth integer inclusively). After that, FF will ask TT what the sum of the subsequence he chose is. The next, TT will answer FF's question. Then, FF can redo this process. In the end, FF must work out the entire sequence of integers. 

Boring~~Boring~~a very very boring game!!! TT doesn't want to play with FF at all. To punish FF, she often tells FF the wrong answers on purpose. 

The bad boy is not a fool man. FF detects some answers are incompatible. Of course, these contradictions make it difficult to calculate the sequence. 

However, TT is a nice and lovely girl. She doesn't have the heart to be hard on FF. To save time, she guarantees that the answers are all right if there is no logical mistakes indeed. 

What's more, if FF finds an answer to be wrong, he will ignore it when judging next answers. 

But there will be so many questions that poor FF can't make sure whether the current answer is right or wrong in a moment. So he decides to write a program to help him with this matter. The program will receive a series of questions from FF together with the answers FF has received from TT. The aim of this program is to find how many answers are wrong. Only by ignoring the wrong answers can FF work out the entire sequence of integers. Poor FF has no time to do this job. And now he is asking for your help~(Why asking trouble for himself~~Bad boy) 

Input

Line 1: Two integers, N and M (1 <= N <= 200000, 1 <= M <= 40000). Means TT wrote N integers and FF asked her M questions. 

Line 2..M+1: Line i+1 contains three integer: Ai, Bi and Si. Means TT answered FF that the sum from Ai to Bi is Si. It's guaranteed that 0 < Ai <= Bi <= N. 

You can assume that any sum of subsequence is fit in 32-bit integer. 

Output

A single line with a integer denotes how many answers are wrong.

Sample Input

10 5
1 10 100
7 10 28
1 3 32
4 6 41
6 6 1

Sample Output

1

題意：有編號為1-n的n個序列，給m個查詢:x y s，每個查詢表示區間[x,y]的和為s

問有多少個有矛盾的詢問

題解（轉自https://dilthey.cnblogs.com/）：

經典的帶權並查集問題；

我們設sum[x]是這n個數的字首和陣列，那麼就可以把所有的 a+…+b = s 都變成 sum[b] - sum[a-1] = s；

那麼我們就可以利用帶權並查集進行進行建樹，照例par[x]代表了節點x的父親節點，而val[x]代表了sum[x] - sum[par[x]]；

首先是find()函式，我們在原來最基礎的並查集find函式中，是有一種類似於把x的父親節點par[x]變成par[par[x]]這樣的，將節點沿著樹枝往上移動的操作，

那麼相應的，我們每次做將par[x]變成par[par[x]]這樣的操作時，val[x]也要修改為val[x]+val[par[x]]；

其次，我們對於每次查詢的結果a,b,s，令 t1 = find(a)，t2 = find(b)，那麼對應的s,val[a],val[b],val[t2]就可以如下圖的向量所示：

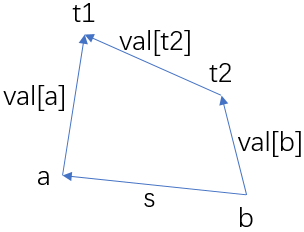
向量的方向相當重要（因為這個WA了兩發= =）：對於任何的從x指向y的向量都代表了sum[x] - sum[y]；

那麼很顯然的有：

①若a,b還不是一個集合內，那麼就要unite他們，即令par[t2]=t1；

　那麼同時，根據向量的加減法，val[t2]也要跟隨著par[t2]的變動，轉變成sum[t2] - sum[t1]；所以根據向量加減的規則就有val[t2] = - val[b] + s + val[a]；

②若a,b已經是一個集合內的，那麼就要判斷是否有矛盾；

　顯然此時t1=t2，那麼如果s是正確的話，就應該有 - val[b] + s = val[a]，否則，s就是一個與前面產生矛盾的、有錯誤的查詢結果；

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<iostream>
#include<map>
using namespace std;
#define N 200010
#define nmax 6
#define inf 0x3f3f3f3f
int fa[N],sum[N]; //sum[x]表示從x到它的根(fa[x])的區間的和
int fin(int x)
{
    if(fa[x]==x)
        return x;
    int t=fa[x];
    fa[x]=fin(fa[x]);
/*因為sum[x]表示從x到它的根(fa[x])的區間的和，所以，當x的根發生改變時，
例如x的根原本是t=fa[x]，即sum[x]原本表示[x,t]這段區間和，這裡的x不一定比t大,現在x的根要指向fy，那麼sum[x]要表示[x,fy]的區間和,則現在的sum[x]=sum[x]+sum[t];
    sum[x]+=sum[t];
    return fa[x];
}
int main()
{
    int n,m;
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        int x,y,s;
        int ans=0;
        memset(sum,0,sizeof(sum));
        for(int i=0; i<=n; i++)
            fa[i]=i;
        for(int i=0; i<m; i++)
        {
            scanf("%d%d%d",&x,&y,&s);
            x--;
            int fx=fin(x);
            int fy=fin(y);
            if(fx!=fy)
            {
                fa[fy]=fx;
                sum[fy]=-sum[y]+s+sum[x];
                /*(1)
                fa[fx]=fy;
                sum[fx]=-sum[x]+s+sum[y];
                */
            }
            else if(sum[y]!=sum[x]+s) 
                ans++;
            /*(2)
            對應（1）處的if語句 
            else if(sum[x]!=sum[y]+s) 
                ans++;
                */
        }
        printf("%d\n",ans);
    }
    return 0;
}