BZOJ 2439: [中山市選2011] 序列
阿新 • • 發佈:2018-11-15
沒人寫過題解?(其實貼吧那個啟發性就夠了233
f[i]表示把1~i改為遞增的最小代價,g[i]表示把i~n改為遞減的最小代價。
不難求出f和g陣列(而且他們是滿足可減性的)。
然後考慮固定一箇中點,左邊和右邊答案分別是什麼
比如說把1~i改成一個倒V的最小代價是
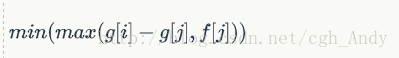
i~n的也同理啊。
然後發現這個各自的決策是有單調性的,畫畫圖就知道了,然後掃一掃就好..
實在不懂就看程式碼?(又短又快呢 現在是最快的233
#include<bits/stdc++.h>
using namespace std;
typedef long 