演算法--最長公共子序列以及子串
問題1:給定兩個字串,求其最大公共子序列
例如asbcdfg和scdfgjkl, 則返回scdfg
使用動態規劃求解,
假設s1=<x1,x2....xn> s2=<y1,y2..ym>
令f[i][j]表示串s1以索引i結尾,串s2以索引j結尾的最長公共子序列的長度。
當i==0或者j==0時,此時s1[i] s2[j]均為空,即有f[i][j]=0
i>=1,j>=1
當s1[i]==s2[j]時,有f[i][j] = f[i-1][j-1] + 1
當s1[i]!=s2[j]時,有f[i][j] = max(f[i-1][j], f[i][j-1])
由於字串s索引從0開始,為了便於計算,描述如下:
f[i][j]表示s1已i結尾,s2已j結尾的最大公共子序列:
i, j=0 f[i][j]=0
當s1[i]==s2[j]時,有f[i+1][j+1] = f[i][j] + 1
當s1[i]!=s2[j]時,有f[i+1][j+1] = max(f[i][j-1], f[i-1][j])
def testl(): s1 = 'sabc' s2 = 'abcs' s = lcs(s1, s2) print (s) def lcs(s1, s2): dp = [[0 for i in range(len(s1)+1)] for i in range(len(s2)+1)] for i in range(0, len(s1)): for j in range(0, len(s2)): if s1[i]==s2[j]: dp[i+1][j+1] = dp[i][j] + 1 else: dp[i+1][j+1] = max(dp[i][j+1],dp[i+1][j]) print (mat(dp)) i = len(s1) j = len(s2) r = [] while i>0 and j>0: #print (i,j,s1[i-1],s2[j-1]) if s1[i-1]==s2[j-1]: r.append(s1[i-1]) i -= 1 j -= 1 elif dp[i-1][j]==dp[i][j]: i -= 1 else: j -= 1 r.reverse() return r
動態規劃陣列如下所示: 表示0sabc 與0abcs的匹配關係:
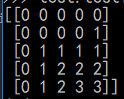
現在找出最大的匹配子序列,
首先最大子序列長度值為dp[len(s1)][len(s2)],此時
若s1[i-1]==s2[j-1],即說明該字元即為公共字元,由於f[i][j] = f[i-1][j-1] + 1 可以沿對角斜向上尋找第二個字元 i-- j--
若兩者不相等,則找出dp[i][j]的來源,由於f[i+1][j+1] = max(f[i][j-1], f[i-1][j]),要麼左邊,要麼上邊,若dp[i-1][j]==dp[i][j]說明來自上面,
則i--,否則j--
最後倒序輸出序列即可。
問題2:給定兩個字串,求其最大公共子串
例如asbcdfg和scdfgjkl, 則返回cdfg 即必須是連續子串
s1=<x1,x2,,xm>
s2=<y1,y2...yn>
令f[i][j]表示s1以i結尾,s2以j結尾的最大公共子串:
i==0 j==0 f[i][j]=0
當s1[i]==s2[j]時,有f[i+1][j+1]=f[i][j]+1
當s1[i]!=s2[i]時,有f[i][j]=0
def lcs2(s1, s2):
dp = [[0 for i in range(len(s1)+1)] for i in range(len(s2)+1)]
row = 0
col = 0
max = 0
for i in range(0, len(s1)):
for j in range(0, len(s2)):
if s1[i]==s2[j]:
dp[i+1][j+1] = dp[i][j] + 1
if(dp[i][j] + 1>max):
max = dp[i][j] + 1
row = i
col = j
else:
dp[i+1][j+1] = 0
print (mat(dp))
return s1[i-max+1:i+1]利用一個變數max來記錄最大子串長度,利用row記錄最大公共子串的最後一個字元在s1中的位置,返回最大公共子串:s1[i-max+1:i+1]
