資料結構——樹——二叉搜尋樹
阿新 • • 發佈:2018-11-16
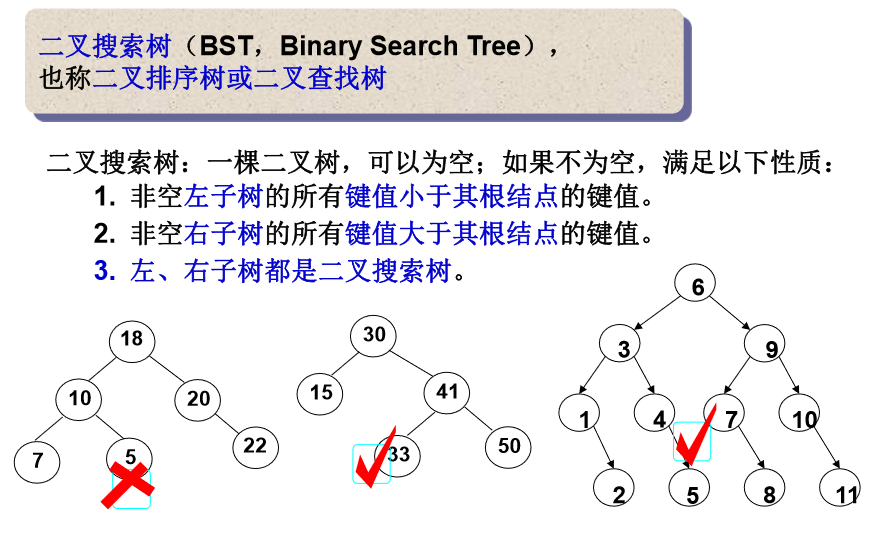
二叉查詢樹(Binary Search Tree),(又:二叉搜尋樹,二叉排序樹)它或者是一棵空樹,或者是具有下列性質的二叉樹: 若它的左子樹不空,則左子樹上所有結點的值均小於它的根結點的值; 若它的右子樹不空,則右子樹上所有結點的值均大於它的根結點的值; 它的左、右子樹也分別為二叉排序樹。
二叉排序樹的查詢過程和次優二叉樹類似,通常採取二叉連結串列作為二叉排序樹的儲存結構。中序遍歷二叉排序樹可得到一個關鍵字的有序序列,一個無序序列可以通過構造一棵二叉排序樹變成一個有序序列,構造樹的過程即為對無序序列進行排序的過程。每次插入的新的結點都是二叉排序樹上新的葉子結點,在進行插入操作時,不必移動其它結點,只需改動某個結點的指標,由空變為非空即可。搜尋,插入,刪除的複雜度等於樹高,O(log(n)).
二叉搜尋樹操作
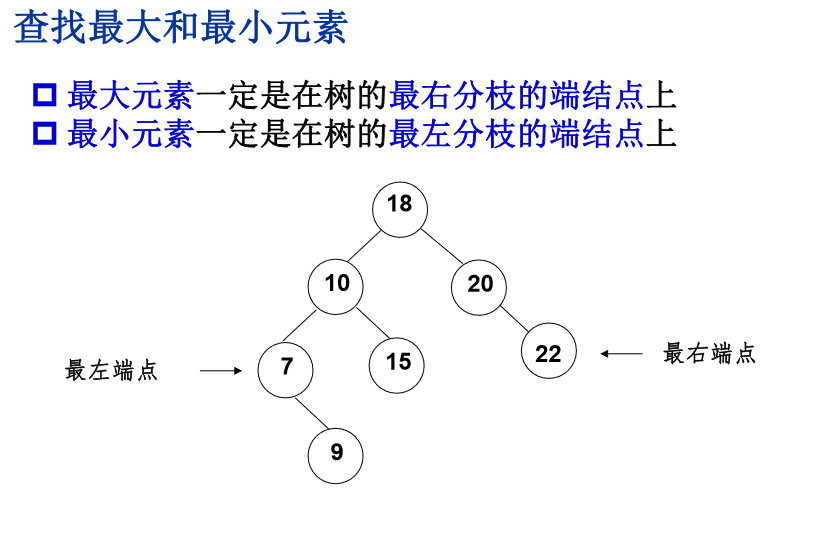
最小元素和最大元素
二叉搜尋樹的插入演算法
BinTree Insert( BinTree BST, ElementType X )
{
if( !BST ){ /* 若原樹為空,生成並返回一個結點的二叉搜尋樹 */
BST = (BinTree)malloc(sizeof(struct TNode));
BST->Data = X;
BST->Left = BST->Right = NULL;
}
else { /* 開始找要插入元素的位置 */
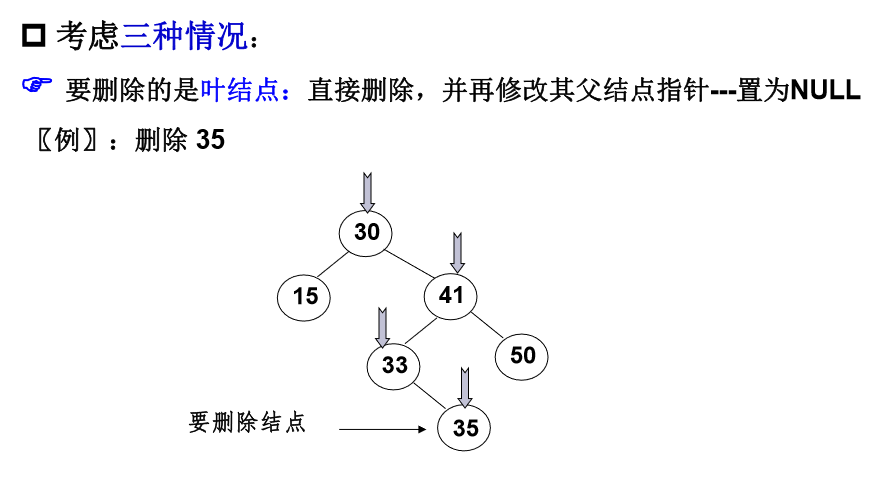
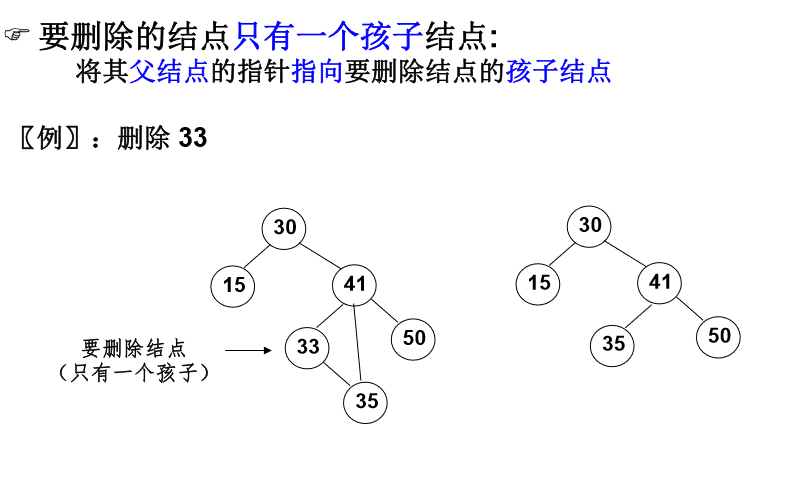
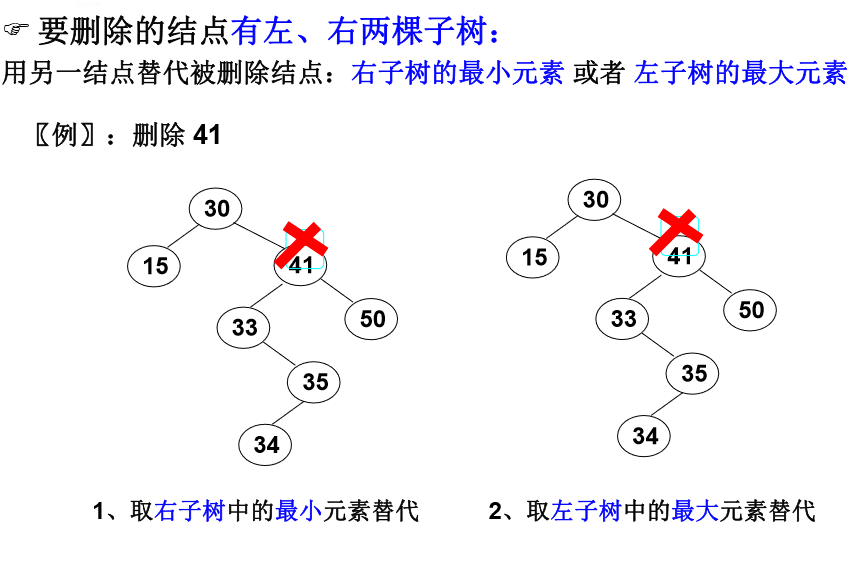
if 二叉搜尋樹的刪除
演算法實現
BinTree Delete( BinTree BST,