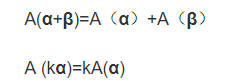文章目錄

• 1、區域性座標系
• 2、世界座標系
• 2.1 為什麼要用矩陣？
• 2.2 模型矩陣（Model Matrix）
• 3、檢視座標系
• 3.1 檢視座標系的定義
• 3.2 檢視矩陣
• 4、投影座標系
• 5、螢幕座標系

1. 我們有什麼？答：模型的初始位置座標（三維座標）。
2. 我們要得到什麼？答：我想要把模型展示在螢幕上展示的二維座標（二維座標）。

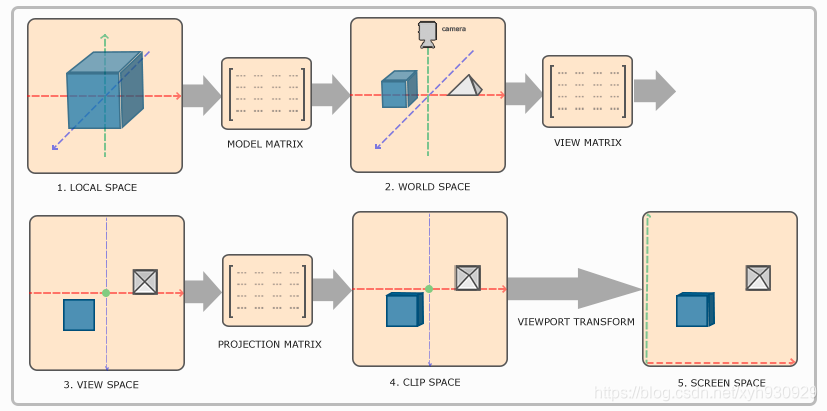
從初始位置座標到平面的二維座標經過了下面的流程，後面逐一介紹。

1、區域性座標系

區域性座標系指的是圖中的LOCAL SPACE，又被稱作本地座標系、本地空間、區域性空間等。總是這就是一個小範圍的概念，描述的只是模型本身的座標。也是模型檔案中儲存的頂點座標所在的座標系。

2、世界座標系

• 世界座標系指的是圖中的WORLD SPACE。剛開始接觸座標變換時，會有這樣的疑問，為什麼要有世界座標系？直接用區域性座標系作為世界座標系為什麼不行？原因是區域性座標系只是相對於單獨一個模型的，當我們想在螢幕上看到很多個模型時，如果我們以某個模型所在的區域性座標系為基準去構造其他的模型，那麼就很有可能會出現所有的模型都疊放在了原點。所以，世界座標用來確定每個模型的區域性座標系的位置。

  也就是每個模型在三維空間中的位置。世界座標系所描述的空間通常會被抽象成"場景"或者"世界"。

• 為了能讓場景中所有的模型都能進行統一的變換，所以必須將所有的模型自身相對於區域性座標系的座標，轉換為相對於世界座標系中的座標。這個過程只要將模型的座標進行相應的平移變換就能得到。而這一步進行的平移變換，就是圖中提到的模型矩陣（Model Matrix），用模型相對於區域性座標系的位置座標右乘一個矩陣就可以得到相對於世界座標系的座標。

2.1 為什麼要用矩陣？

到這裡應該有個疑問，為什麼平移要用到矩陣？其實不光是平移，模型在場景中的伸縮、旋轉、檢視變換、投影變換也是通過矩陣變換來做的。應用矩陣來計算這些變換的原因如下：

1. 線上性代數中，所有的線性變換（見下面解釋）都可以通過構造一個矩陣，並以矩陣乘法的方式完成。
2. 在圖形變換中，涉及到就是空間對映（通過一個座標系空間的座標求出對應另外一個座標系中的座標就是空間對映）和頂點變換，這這種變換都是線性變換。
3. 所以，正好可以將圖形中的變換應用線性代數中的矩陣變換來計算，這樣做可以將所有的變換都統一成矩陣變換，也方便GPU在計算座標時進行優化。

線性變換的概念。

• 線性變換：指的是一個向量空間V到自身的對映。換句話說，一個n維向量在經過線性變換以後仍然是n維向量的變換，並不會導致它變成n+1維或者更大維度的向量。線性變換的數學定義——線性空間V上的一個變換A稱為線性變換，對於V中任意的元素α，β和數域P中任意k，都有：
  

2.2 模型矩陣（Model Matrix）

在模型頂點座標由區域性座標系變換到世界座標系的過程中。可以只經過平移變換來進行。除此之外，在這一過程中，也可以隨模型的形態進行設定，例如伸縮、旋轉等。

首先來看最簡單的伸縮變換：假設有一個頂點的座標為(x,y,z)，那麼將該點的x、y、z分別在其分量上伸縮 $S_x$、 $S_y$、 $S_z$，則變換過程如下：

$\left[ \begin{matrix} x*S_x \\ y *S_y\\ z *S_z \end{matrix} \right] = \left[ \begin{matrix} S_x &0 &0\\ 0 &S_y & 0\\ 0 &0&S_z \end{matrix} \right]*\left[ \begin{matrix} x \\ y \\ z \end{matrix} \right] = \left[ \begin{matrix} x_1 \\ y_1 \\ z_1 \end{matrix} \right]$

發現伸縮的過程是可以寫成一個頂點座標左乘一個 $3*3$矩陣（矩陣的乘法可參考這篇文章圖形變換中涉及到的數學知識）來實現的。再看一下平移的過程：發現一個問題，如果像伸縮一樣來處理平移變換，是沒有辦法將平移變換寫成 $3*3$矩陣右乘的形式的。
$\left[ \begin{matrix} x+T_x \\ y +T_y\\ z +T_z \end{matrix} \right] = \left[ \begin{matrix} x_1 \\ y_1 \\ z_1 \end{matrix} \right]$

解決此問題的方法是用齊次座標（可參考這篇文章圖形變換中涉及到的數學知識）來表示頂點座標，給頂點座標加一個維度再進行相應的計算，就可以將平移變換的過程轉化成下面的流程。

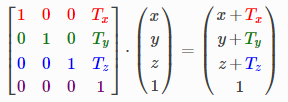
同樣，為了保證統一，伸縮的過程可以轉換為：

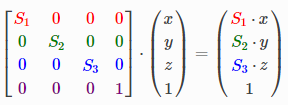
旋轉過程的變換矩陣有三種，分別是沿著x、y、z軸進行旋轉的矩陣（三個矩陣的由來可參考這篇文章圖形變換中涉及到的數學知識）：

3、檢視座標系

       人眼在觀察一個物體，在不同角度不同位置去觀察，看到的效果是不一樣的。所以，在三位場景中，我們除了定義模型本身以外，還需要定義觀察點位置、觀察方向等。定義完觀察點的相關資訊以後，就可以得到一個在該觀察點位置所看到場景狀態。這個場景的每個位置的座標也是需要定義的。而定義這個影象座標的座標系，被成為檢視座標系。

3.1 檢視座標系的定義

• 觀察點位置（ $viewPosition$）：世界座標中的一個位置座標。
• 觀察點方向（ $viewDirection$）： $viewDirection=viewPosition-worldOrigin$，觀察點方向等於觀察點位置減去世界座標原點。
• $z$軸： $viewDirection$所在直線作為檢視座標系的z軸。該方向為z軸負方向， $-viewDirection$為z軸正方向。
• $x$軸：以觀察點為始點，沿著世界座標系的y軸，去一個向量，我們稱為UpDirection。用 $viewDirection$和 $UpDirection$進行叉乘，可以得到x軸（為什麼叉乘可以得到x軸可參考這篇文章圖形變換中涉及到的數學知識）。
• $y$軸：用z軸和x進行叉乘就可以得到y軸了。

叉乘的幾何意義：兩個向量叉乘可以得到一個與兩個向量都垂直的一個向量。

3.2 檢視矩陣

       檢視矩陣（流程圖中的View Matrix），使用矩陣的好處之一是如果你定義了一個座標空間，裡面有3個相互垂直的軸，你可以用這三個軸外加一個平移向量來建立一個矩陣，你可以用這個矩陣乘以任何向量來變換到那個座標空間。這正是檢視矩陣（流程圖中的View Matrix）所做的，現在我們有了3個相互垂直的軸和一個定義攝像機空間的位置座標，我們可以建立檢視矩陣了。

4、投影座標系

• 以上的變換都是針對三維的頂點座標進行變換。但是最終我們呈現在螢幕上的影象是一個二維座標。將一定範圍內的座標轉化到標準化裝置座標系的過程(而且它很容易被對映到2D觀察空間座標)被稱之為投影(Projection)，因為使用投影矩陣能將3維座標投影(Project)到很容易對映的2D標準化裝置座標系中。

• 除了將三維座標轉換成二維座標以外，場景中的模型座標並不是所有的點都需要被呈現出來，因為螢幕的大小是固定的，如果模型被擴大了很多倍，或者場景內的模型非常多，不可能將場景內的內容全部都呈現出來，需要將場景