參考：條件獨立與MRF
參考：置信傳播
參考：Markov Logic Networks
參考：概率圖模型
參考：MLN+舉例

摘要：我們提出一個簡單的方法將一階邏輯和概率圖解模型組合成一種表示形式。馬爾科夫邏輯網就是一個每個準則或語句都有權重的一階邏輯知識庫，其中常數代表庫中物件，還約定了一個基本馬爾科夫網知識庫中一個一階邏輯準則的每個可能的基元都帶有相應的權重。馬爾科夫邏輯網推理是通過在回答問題所需的最小基元子集上運用馬爾科夫鏈蒙特卡羅方法實現的。權重是從關係資料庫通過擬似然度量的優化迭代高效學習獲得，可選擇地，額外的子句可運用歸納邏輯程式技術學得。使用一所大學內的一個真實世界資料庫和知識庫的實驗表明這種方法大有前途。

關鍵詞：統計關聯學習，馬爾科夫網，馬爾科夫隨機場，對數線性模型，圖模型，一階邏輯，可滿足性， 歸納邏輯程式設計，基於知識的模式構建，馬爾科夫鏈蒙特卡羅方法，擬似然，連線預測

介紹

將概率和一階邏輯一起表達一直是人工智慧界的目標。概率圖模型使我們能有效地應對不確定性，一階邏輯讓我們能簡潔地表達廣博的知識，而往往許多應用中兩者都需要。近年來，這個問題由於和統計關係學習 (Getoor & Jensen, 2000; Getoor & Jensen, 2003; Dietterich等, 2003), 或者多關係資料探勘(Dzeroski & De Raedt, 2003; Dzeroski等, 2002; Dzeroski等, 2003; Dzeroski & Blockeel, 2004)的相關性引起了廣泛興趣。當前的提議一般都集中在將概率和一階邏輯的有限子集組合在一起，如霍恩子句(e.g., Wellman等 (1992); Poole (1993); Muggleton (1996); Ngo and Haddawy (1997); Sato and Kameya (1997); Cussens (1999); Kersting and De Raedt (2001); Santos Costa 等(2003))，基於框架的系統(e.g., Friedman等 (1999); Pasula and Russell (2001); Cumby and Roth (2003))，或者資料查詢語言(e.g., Taskar等(2002); Popescul and Ungar (2003))，它們都很複雜。在本論文中，我們介紹了馬爾科夫邏輯網，這是一個除了有窮集要求外沒有其它限制的能將概率和一階邏輯結合的非常簡單的表示辦法。我們為馬爾科夫邏輯網的學習和推理開發了高效的演算法，並在某個現實世界場景中進行了評估。

一個馬爾科夫邏輯網就是一個每個準則都有權重的一階邏輯知識庫，可看成是構建馬爾科夫邏輯網路的模板。從概率的視角看，馬爾科夫邏輯網提供一種簡潔的語言來定義大型馬爾科夫網，能靈活地、模組化地與大量知識合併；從一階邏輯的視角看，馬爾科夫邏輯網能健全地處理不確定性、容許有瑕疵甚至矛盾的知識庫，降低脆弱性。有許多統計關係學習領域的重要任務，如集合分類、連結預測、連結聚合、社會網路建模和物件識別，都自然而然地成為運用馬爾科夫邏輯網推理和學習的例項。

現實世界資料庫和知識庫的試驗顯現了馬爾卡夫邏輯網相對於純邏輯方法或純概率方法的優勢。本論文的開頭簡要介紹馬爾科夫網（第二章）和一階邏輯（第三章）的基礎，核心部分介紹了馬爾科夫邏輯網及其推理和學習的演算法（第四-六章），接下來是試驗結果的報告（第七章），最後，我們介紹了怎樣利用馬爾科夫邏輯網來完成各種統計關聯學習任務（第八章），還討論了馬爾科夫邏輯網與以前一些方法的關係（第九章），最後列出了一些下一步工作的方向（第十章）。

馬爾科夫網路

馬爾科夫網（也叫馬爾科夫隨機場）是隨機變數集x=x1,x2,…,xn的聯合分佈模型(Pearl, 1988)，它由一個無向圖G和一個勢函式Фk集合組成，每個隨機變數是圖上的節點，圖的每個團在模型中都有一個勢函式，勢函式是一個非負實函式，它代表了相應的團的狀態。馬爾科夫網的聯合分佈如下

$P(X=x)=\frac{1}{Z}\prod_{k} \phi_k(x_k )$ (1)

其中x{k}是團中隨機變數的狀態，Z也叫配分函式（態和），定義為Z 。將馬爾科夫網路中每個團的勢用狀態的所有特徵值加權後求和再取冪，就可方便地表示成對數線性模式

$P(X=x)=\frac{1}{Z}exp(\Sigma_j \omega_jf_j(x))$

特徵函式可以是表示狀態的任何實函式，本論文將只討論二元特徵值。公式一是勢最直接的表示，其中每個團每個可能的狀態都有一個對應的特徵值 fj(x)，它的權重是wj，這種表示方法與團數量的冪相關。可是，我們可以自由地運用一些方法比如狀態的邏輯函式等減少特徵值數量，特別在團數量很大時能相比勢函式方式提供一種更簡潔的表示形式。馬爾可夫邏輯網路就是利用了這一方式。

馬爾可夫網的推理是NP完備問題(Roth, 1996)。最被廣泛使用的近似推理方法是馬爾可夫鏈蒙特卡羅法（MCMC）(Gilks等, 1996)，特別是吉布斯取樣法，它依次對每個隨機變數在它們各自的馬爾可夫毛毯中進行取樣處理（一個節點的馬爾可夫毛毯是一個節點能與剩餘網路互相獨立的最小節點集合，簡單地說在一個馬爾可夫網中，就是節點在圖中的鄰居）。邊緣概率可通過對取樣值的計數得到，而條件概率可將作為條件的隨機變數值設定後運用吉布斯取樣得到。另外一種流行的馬爾可夫網推理方法是置信傳播法(Yedidia等，2001)。

求馬爾可夫網權重的最大概似法或者最大後驗概率法都不是封閉解，但是由於對數概似函式是權重的凹函式，可運用標準積分或優化的擬牛頓法高效求解 (Nocedal & Wright, 1999)。另一種選擇是迭代法(Della Pietra等, 1997)。特徵值可從資料中學得，比如通過貪婪地構建原子特徵合取式(Della Pietra等，1997)。

一階邏輯
一個一階知識庫是一個由一階邏輯句子或規則組成的集合。組成規則的有四種類型的符號：常數、變數、函式和謂語，常數符號代表所涉及領域的物件（例如,人:安娜,鮑勃,克里斯,等等），變數符號可在涉及領域的物件範圍內變化，函式符號（例如，MotherOf）表示了物件組之間的對映關係，謂語符號代表了物件間的關係（如，Friends）或者物件的屬性（如，Smokes），還需要說明哪些符號代表了域中的哪些物件、函式和關係。變數和常數可以有型別，那樣的話常數只能代表同類型的物件，變數只能在同類型的物件範圍中取值，例如，變數x可以代表人（如，安娜，鮑勃等），常數C可以表示一個城市（如，西雅圖）。

一個詞是代表域中物件的任意表達式，它可以是常數，變數或應用到一組詞上的函式，比如，安娜、X、GreatestCommonDivisor（x，y）都是詞。一個原子規則或原子是應用到一組詞上的謂語（Friends（x，MotherOf(Anna)））。而規則是使用數量詞和邏輯連線符從原子規則遞迴構建的。如果F1和F2是規則，那麼下列的也是規則： ¬ F1（否定），當且僅當F1為假時取真值； F1 ∩ F2（合取），當且僅當F1和F2都為真時取真值； F1 ∪ F2 （析取），當且僅當F1或F2為真時取真值； F1 ⇒ F2 （蘊涵），當且僅當F1為假或F2為真時取真值；F1 ⇔ F2（等價） ，當且僅當F1和F2取值一樣時取真值； ∀ x F1（全稱量詞），當且僅當F1對域中每個物件X為真時取真值； ∃ x F1（存在量詞），當且僅當F1對域中至少一個物件X為真時取真值。圓括號可用來確保優先順序。知識庫中的規則之間隱含合取關係，因此可以說一個知識庫就是一條巨大的規則。一個基詞是一個不含變數的詞，一個基本原子或基本謂語是一個引數都是基詞的原子規則。一個可能世界或者海爾勃朗解釋為每個可能的基詞賦真值。

一個規則如果是可滿足的，那麼當且僅當至少在一個世界中是真的。一階邏輯中基本的推理問題一般是確定一個知識庫KB是否包含某個規則F，也就是在KB所有真的世界裡F也真。這個常常用反證法證明：KB包含F當且僅當KB包含¬F無法滿足。（於是，如果一個知識庫含有矛盾，所有的規則也就矛盾了，因此，知識庫需要非常盡心維護）。為了方便自動推理，規則常常被轉換成一種正則形式，一種句子形式（也叫做合取正規化（CNF））。一個正規化的知識庫是由一些合取的句子組成，而每個句子又由析取的文字組成。每個一階邏輯的知識庫都可通過機械的步驟轉換成正規化。在一階邏輯中正規化用於問題求解，這是一個健全的、無法反駁的推理方法。

基於一階邏輯的推理僅是半可解的，因此，知識庫往往使用一階邏輯的有更多特性的限定子集來表示。霍恩子句是一種最被廣泛使用的子集，它的句子只允許最多一個肯定的文字。Prolog程式語言就是基於霍恩子句邏輯（Lloyd, 1987），Prolog程式可以從庫中搜索含有近似資料的霍恩子句，這在歸納邏輯程式研究過（Lavrac & Dzeroski, 1994）。

表Ⅰ是一個簡單的知識庫和它的正規化轉換形式。請注意，這些規則在現實世界中通常是真的，但不總是真的。在大多數場景一些重要的規則往往很難表達為一直為真，這些規則僅捕捉到了相關知識的一部分。儘管善於表達，但是純粹的一階邏輯在人工智慧實踐中應用能力有限。許多特別的擴充套件辦法被提出來解決這個問題，這個問題在更有限的命題邏輯範圍內已被概率圖模型很好地解決了。下一節將介紹將這些模型推廣到一階邏輯的辦法。
表Ⅰ是一階邏輯知識庫和馬爾可夫邏輯網的例子，Fr、Sm、Ca分別是Friends、Smokes和Cancer的縮寫

English	一階邏輯語言	正規化	權重
Friends of friends are friends.	∀ x∀ y∀ zFr(x,y)∧Fr(y,z)⇒Fr(x,z)	¬Fr(x,y)∨¬Fr(y,z)∨Fr(x,z)	0.7
Friendless people smoke.	∀ x(¬(∃yFr(x,y))⇒Sm(x)	Sm(x)∨Fr(x,g(x))	2.3
Smoking causes cancer.	∀ xSm(x)⇒Ca(x)	¬Sm(x)∨Ca(x)	1.5
If two people are friends,either both smoke or neither does.	∀ x∀ yFr(x,y)⇒(Sm(x)⇔Sm(y))	¬Fr(x,y)∨Sm(x)∨¬Sm(y)	1.1 1.1

馬爾科夫邏輯網

一個一階邏輯知識庫可以看作是在一系列可能的世界上加上了一套硬約束：哪怕只與一條規則衝突也不行。馬爾科夫邏輯網的基本想法就是要軟化這些約束：一個可能世界如果與知識庫規則衝突，不會不可能存在，而是可能性下降，衝突的規則數越少，可能性越大。每個規則都和一個反映其約束強度的權重關聯：在其它情況一樣的前提下，權重越高的，滿足和不滿足此規則的事件的對數概率差就越大。

定義4.1 馬爾科夫邏輯網L是（Fi，wi）對的集合，其中 Fi代表一階邏輯規則， wi是一個實數；有限的常數集為C = {c1,c2,…cn}，馬爾科夫網ML,C如下1、2來定義：

1、L中每個謂詞的每個可能基元在ML,C中有一個二元節點，如果原子公式為真，節點的值就等於1，否則為0。

2、L中每個規則的每個基本可能在ML,C中有一個特徵值，當這個規則為真時等於1，否則等於0，特徵值的權重為 Fi 對應的wi。

馬爾科夫網MLN中規則的語法是一階邏輯的標準語法(Genesereth & Nilsson, 1987)，自由（未限定）變數被認為是規則最外層的全稱變數。

這個定義可以看作構建馬爾科夫網路的模板。如果常數集不同，它會產生大小不同的網路，但是所有關於結構和引數的規則都是確定的（比如一個規則的所有可能都有相同的權重）。我們把它稱作基本馬爾科夫網，以示與一階邏輯MLN的區別。從定義4.1、等式1和2可以得出，基本馬爾科夫邏輯網概率分佈如下

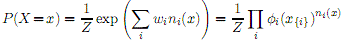
ni(x)是Fi在X中所有取真值的基本規則的數量，而x{i}是Fi中為真的原子，又有ϕi(xi)=ewi。請注意，雖然我們將馬爾科夫邏輯網定義成對數線性模式，它們還可以定義成勢函式積的樣子，就如上面第二個等式。當硬約束和軟約束並存時，這是最簡便的方法（比如，當一些規則很確定時，不滿足將導致事件不可能）。

按照定義4.1構建的ML,C的圖結構是這樣的：當且僅當兩個節點相應的基本原子同時出現在L中的一個規則的至少一個基本形式時，這兩個節點之間就有一條邊。這樣，ML,C的每個基本公式中的原子構成一個（未必最大的）集團。

圖1展示了一個基本的馬爾科夫網，它是由表1的最後兩個規則和常數Anna和Bob定義的。圖中的每個節點都是基本原子（比如，Friends(Anna，Bob)）。當一對原子同時出現在某個基本規則時，它們之間就有一條弧。這個ML,C可以用來推測當知道Anna和Bob的吸菸習慣時他們朋友的可能性，或者當他們是朋友同時Anna有癌症時Bob得癌症的概率，等等。

ML,C的每個狀態代表了一個可能的世界，一個可能的世界就是一個物件集合、一個函式集合（對映物件組）和一組物件之間的關係；它們一起來確定每個基本原子都取真值。下面的幾個假設保證了代表（L,C）的可能世界集是個有限集，又很好的獨特定義了這些可能世界的概率分佈，同時還與所涉領域和表達形式無關。這些假設在絕大多數實踐應用中是合理的，大大簡化了馬爾科夫邏輯網的應用難度。有賴於此，我們可以輕鬆地討論後面的幾個例子。

假設1：命名唯一性。不同的常數代表不同的物件（Genesereth & Nilsson，1987）。

假設2：範圍封閉性。只存在能用（L，C）中常數和函式符號表示的物件（Genesereth & Nilsson，1987）。

假設3：函式確定性。L中每個函式每個可能的值都確定在常數集C中。

最後這個假設可以讓我們在基本化規則時將函式替換成它們的值，就只需考慮以常數作為引數的基本原子，這樣就可以忽略（L,C）中所有的函式和常數（海爾勃朗全域）構建無限原子集的情況，因為每個詞都是C中確定的常數，包含它們的原子也就表示為包含對應的常數。 按定義4.1每個謂詞的可能基形可以這樣簡單得到，將變數用C中常數替換，將函式也用相應的常數替換。表Ⅱ是在假設1、2、3基礎上求基本原子規則的步驟。如果一個規則多於一條子句，那麼它的權重在各個子句上平分；而一個句子的權重會被賦予它的每個基本形式。

表II 基本原子的構建

function Ground(F, C)

inputs: F, a formula in first-order logic

           C, a set of constants

output: GF , a set of ground formulas

calls: CNF(F,C), which converts F to conjunctive normal form, replacing existentially quantified formulas by disjunctions of their groundings over C

F ← CNF(F, C)

GF = Φ

for each clause Fj ∈ F

    Gj = {Fj}

    for each variable x in Fj

        for each clause Fk(x) ∈Gj

            Gj ← (Gj \ Fk(x)) ∪ {Fk(c1), Fk(c2),..... Fk(cj)g} ，where Fk(ci) is Fk(x) with x replaced by ci ∈ C

    GF ← GF ∪ Gj

for each ground clause Fj ∈GF

    repeat

        for each function f(a1,a2,.....) all of whose arguments are constants

            Fj ← Fj with f(a1,a2,......) replaced by c, where c = f(a1,a2,......)

    until Fj contains no functions

return GF

假設1（命名唯一性）可以去掉，如果引入等於謂詞（Equals(x,y)或x=y）並將等於的自反、對稱和傳遞性，以及對於任意二元謂詞P，clip_image012，其餘高階的謂詞和函式也一樣，這些公理加入馬爾科夫邏輯網的話（Genesereth & Nilsson，1987）。每對常數在最終形成的馬爾科夫邏輯網中都有一個節點，1代表這對常數是同一物件，否則為0；這些節點之間以及和網路的其它部分的連線弧代表了上述的公理。這讓我們有能力對兩個常數的等同性進行概率推理，併成功地以此法為基礎進行了物件識別（請參閱8.5節）。

如果知道未知物件的數量u，我們可以簡單地引入u個任意新常數，這樣假設2（範圍封閉性）就可以去掉了。如果u不確定但是有限的，假設2也可以不用，辦法是引入u的概率分佈，用每個未知物件的數量對馬爾科夫邏輯網基本化，規則F的概率可計算為clip_image014，MuL，C是有u個未知物件的基本馬爾科夫邏輯網。而u如果無限的話，就需要將馬爾科夫邏輯網擴充套件至無限常數集條件下。

讓HL,C代表由L中的符號、（L，C海爾勃朗全域）中的常數構建的所有基詞。如果將HL,C的每個物件看作常數，採取去掉假設1相同的步驟的話，假設3也可以去掉。例如，函式G(x)、常數A和B，這個馬爾科夫邏輯網將有節點G(A)=A、G(B)=B等。這有可能引入無限多的新常數，需要相應擴充套件馬爾科夫邏輯網。但無論如何，如果我們限定最大巢狀層數的話，得到的馬爾科夫邏輯網還是有限的。

總之，只要範圍是有限的，那麼假設1-3都可以不要。我們相信馬爾科夫邏輯網能擴充套件到無限領域（Jaeger（1998）），不過那主要是理論研究領域的事，我們以後再考慮。除非另外註明，本論文的接下來部分都基於假設1-3。

簡單地將一個一階邏輯知識庫的每個規則賦予權重，這個庫就變成一個馬爾科夫邏輯網。例如，利用表Ⅰ最後兩行的句子和權重構建的馬爾科夫邏輯網， 當其它條件相同時，根據這個馬爾科夫邏輯網可以得出，n個沒有朋友的人不吸菸的概率要比所有沒有朋友的人都抽菸的概率小e(2.3)n倍。值得注意的是，表Ⅰ的那些帶全稱量詞的規則在現實世界都是錯的，但是作為馬爾科夫邏輯網的特徵來看的話，卻抓住了朋友友誼和吸菸習慣間的有用資訊。比如，青少年朋友傾向於有相同的吸菸習慣（Lloyd-Richardson等，2002）。事實上，像表Ⅰ這樣一個馬爾科夫邏輯網簡潔地表示了一個社會關係分析中的一個主要模型（Wasserman & Faust，1994）。

顯而易見，馬爾科夫邏輯網包含了命題邏輯概率模型的所有要素，下面詳細說明。

命題 4.2：任意離散或有限精度的數字隨機變數的概率分佈都能用馬爾可夫邏輯網表達。

證明：首先考慮布林型的隨機變數（X1，X2，…，Xn）；我們為每個變數Xh定義一個不含引數的謂詞Rh，再將表示（X1，X2，…，Xn）每個狀態的規則加入到L中；這個規則是n個字的合取，當Xh為真時這個字取Rh()，否則取 ¬ Rh()，這個規則的權重為logP（X1，X2，…，Xn）（如果某些狀態概率為0，我們就採用乘積形式，見等式3，用ϕi()表示i狀態的概率）；因為L中所以謂詞都沒有引數，L所定義的馬爾科夫邏輯網每個變數Xi 就是一個節點，而且這個ML,C與常數C無關；對於任一狀態，相應規則為真，其它規則為假，這樣等式3就代表了初始分佈（注意Z=1）。只要為每個變數定義一個沒有引數的謂詞，將上述方法推廣到任意離散變數就很簡單直接；有限精度數字隨機變數也一樣，只要用布林矢量表示這些變數就可以了。（證畢）

當然，只要為相應的要因定義規則（馬爾科夫網的任意特徵、節點狀態以及貝葉斯網路中的父節點），象馬爾科夫網、貝葉斯網這樣的緊湊要因模型仍然能用馬爾科夫邏輯網簡潔地表示。

一階邏輯（在假設1-3下）是馬爾科夫邏輯網的一個特例，下面將接著討論，這個特例的所有權重都相等且趨向無限大。

命題4.3 設KB是一個可滿足的知識庫，L是一個所有規則都帶有權重的代表KB的馬爾科夫邏輯網，C代表KB中出現的常數集，Pw(x)是由ML,C得出的事件集x的概率，XKB是滿足KB的事件集，F為一階邏輯的任意規則，那麼有：

1、∀ x∈XKB limw→∞ Pw(x) = |XKB|-1

∀ x∉XKB limw→∞ Pw(x) = 0

2、∀ F KB蘊含F當且僅當 limw→∞ Pw(F) = 1

證明：設k為ML,C中基本規則的數量，利用等式3，若x∈XKB則Pw(x)=ekw/Z，若 x∉XKB則Pw(x)≤e(k-1)w/Z；所有x∈XKB等概率，又limw→∞ P(x\XKB)/P(XKB)≤ limw→∞ P(|x\XKB|)/P(|XKB|)e-w=0（第一點證畢）。由蘊含的定義，所有滿足KB的事件也滿足F，設XF為滿足F的事件集，那麼有 XKB⊆XF，而Pw(F) = Pw(XF) ≥ Pw(XKB)，由第一點limw→∞ Pw(XKB) = 1，所以，limw→∞ Pw(XF) = 1；反過來，如果 limw→∞ Pw(XF) = 1，那麼每個非零概率的事件極限上必須滿足F，這就包含了 XKB中 所有的事件。（證畢）

換句話說，在所有相等的無窮大權重的極限中，馬爾科夫邏輯網表示了滿足知識庫的所有事件的一個均勻分佈，所有蘊含問題可以通過計算問題規則的概率是否為1來判斷。即使在權重是有限值的情況下，從下面的觀念來看，一階邏輯已被植入到了馬爾科夫邏輯網中。不是一般性，我們假設權重都是非負的（若一個規則的權重w為負值，我們就用它的否定形式來替換，這時權重為-w），如果一個由馬爾科夫邏輯網L中規則構成的知識庫是可滿足的，那麼，對於任意常數集C來說，滿足情況的模式分配就是馬爾科夫邏輯網所代表的概率分佈，這是因為這些模式都是有最大值∑iwini(x)（見等式3）的事件，這個表示式在所有規則的所有可能為真時取最大值（比如，滿足知識庫）。但不管怎樣，馬爾科夫邏輯網和通常的一階邏輯知識庫不一樣，當包含矛盾的規則時，它也能產生有用的結果。一個馬爾科夫邏輯網也可以通過一些知識庫的合併來獲得，即使這些知識庫有部分不相容。這個特性在某些領域非常有潛力，如語義網（Berners-Lee et al.，2001）和大規模協作（Richardson & Domingos，2003）。

有一個馬爾科夫邏輯網一般化一階邏輯的簡單而有趣的例子，設一個馬爾科夫邏輯網只有一條規則：∀x R(x)⇒ S(x)、權重為w，常數集C = {A}；這裡只有4個事件：{¬R(A)，¬S(A)}、{¬R(A)，S(A)}、{R(A)，¬S(A)}、{¬R(A)，S(A)}，從等式3可以得出：P({R(A)，¬S(A)})=1/(3ew+1)、其它三個事件的概率是ew/(3ew+1)（除數是配分函式Z，見第二章）；這樣，如果w>0，這個馬爾可夫網使得與∀x R(x)⇒ S(x)不一致的事件比其它的三個可能性更低一些；從上我們得到P(S(A)|R(A)) = 1/(1+e-1)，limw→∞P(S(A)|R(A)) = 1，又回到了一階邏輯的結果。

實踐中，我們發現將每個謂詞單獨加到馬爾可夫邏輯網中非常有用。換句話說，對於謂詞R(x1,x2,…)，我們加入規則∀x1,x2… R(x1,x2,…)，權重為wR，這使得單句的權重能與謂詞邊際分佈較好地匹配，讓那些非單句的權重僅依賴與相關的謂詞。

如果對權重有一些直覺上的理解，那麼對我們手工構建或閱讀學習一個馬爾可夫邏輯網就有幫助。簡單地說，一條規則F的權重就在其它條件不變時為真或為假的對數差異。然而，F往往和其它規則有著共同的變數，想要反轉F同時保持其它規則不變往往不太可能，規則F的概率和它的權重之間也就不再存在一對一關係。不過，如果我們從最大熵分佈的約束或者從學習經驗概率的最大似然權重來看，總的來說所有規則的概率決定了所有的權重（Della Pietra et al.，1997）。因此設定馬爾可夫邏輯網的權重最好的辦法是：寫下每個規則應有的概率，把它們當做經驗頻率，然後運用第六章的演算法來學習這些權重；相反地，從一個馬爾可夫邏輯網學習到的權重從統計上可以看作暗含著規則的經驗概率。

如果使用型別化的常數和變數，由於只需要將變數基本化為相同型別的常數，那麼，基本馬爾可夫邏輯網的大小可以大大減小。不過，即使這樣網路還會非常巨大。幸運的是，正如下一章節介紹的，有許多推理問題並不需要基本化整個馬爾科夫邏輯網來解決。

推理

馬爾科夫邏輯網可以回答類似“規則F2成立的前提下，規則F1成立的概率是多少？”的任意問題。如果F1和F2是一階邏輯的兩個規則，C是出現在F1、F2中的常數的有限集合，而L代表馬爾科夫邏輯網，那麼

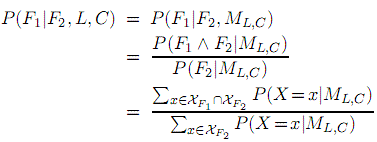
其中XFi是Fi成立的事件集，P（X=x|ML,C）由等式3得出。一般圖形模型中的條件查詢都是等式4的特例，其中F1、F2和L中的謂詞都沒有引數，而且規則都是合取式。在一階邏輯中一個知識庫是否蘊含規則F實際上就是P（F|LKB,CKB,F）是否等於1的問題，LKB是將知識庫中所有規則權重都設成無窮大後等到的馬爾科夫邏輯網，CKB,F是KB或F出現的常數集合。在F2成立的條件下，利用等式4計算出P（F|LKB,CKB,F）就能回答這個問題。

即使在規模很小的領域直接利用等式4來計算都是棘手的，因為馬爾科夫邏輯網推理包含了#P-complete複雜度的概率推理，而邏輯推理在有限域也是NP-complete複雜度的，所以不能寄予期望。可是，提高推理運算效能的許多大數技術都可以運用到馬爾科夫邏輯網上，這是因為馬爾科夫邏輯網能使用細粒度的知識庫，包含了上下類的獨立性，推理就要比普通的圖模型更有效；在邏輯方面，具備了概率語義的馬爾科夫邏輯網能夠進行高效的近似推理。

原則上，P（F1|F2，L，C）可以使用馬爾科夫蒙特卡洛演算法近似得出，只要拒絕轉移到F2不成立的狀態，計數F1成立的取樣即可。但即使這樣對於任意規則，這種演算法還是太慢了。當F1和F2都由基詞的合取式組成時，我們準備了一個的演算法來替代，雖然沒有等式4的普遍性，但現實中的問題往往是這種形式，而且我們回答問題時將比直接應用等式4更有效率。研究提高的演算法（比如要回答的問題含有變數）（參閱Jaeger（2000）和Poole（2003）最初的研究成果）是將來的一個重要研究方向。和知識庫模式構建（Wellman等，1992）類似，這個演算法分為兩個階段。第一階段求得計算P（F1|F2，L，C）所需基本馬爾科夫邏輯網的最小子集M，如表Ⅲ所示。任何事實上為真的基本規則可以忽略，相應的弧也可以省略掉，這樣等到的網路規模就大大縮小了，演算法也就很快了。在最壞的情況下，得到的網路有O（|C|a）個節點，其中a是所有謂詞的最大引數數量，實踐中a往往很小。

表Ⅲ 馬爾科夫邏輯網推理中的網路構建

function ConstructNetwork(F1, F2, L, C)

inputs: F1, a set of ground atoms with unknown truth values (the “query”)

            F2, a set of ground atoms with known truth values (the “evidence”)

            L, a Markov logic network

            C, a set of constants

output: M, a ground Markov network

calls: MB(q), the Markov blanket of q in ML,C

G ← F1

while F1 ≠ ∅

for all q ∈ F1

    if not q ∈ F2

        F1 ← F1 ∪ (MB(q)\G)

       G ← G ∪ MB(q)

    F1 ← F1 \ {q}

Return M, the ground Markov network composed of all nodes in G, all arcs between them in ML;C, and the features and weights on the corresponding cliques

第二階段將F2相關節點設為F2成立的值，然後進行推理。我們應用的是吉布斯取樣法，但是其它推理方法也可以使用。基本吉布斯方法是在一個基本原子的馬爾科夫毛毯範圍內對它進行取樣。一個基本原子的馬爾科夫毛毯是和它一起出現在某些基本規則中的基本原子集合。一個基本原子Xl在它的馬爾科夫毛毯Bl狀態為bl時的概率為

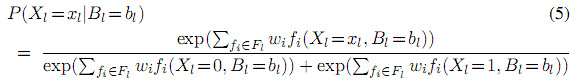
其中Fl是Xl出現的基本規則集合，fi（Xl=xl，Bl=bl）是當Xl=xl，Bl=bl時第i個基本規則的特徵值（0或者1）。對於那些在某些事件中確定為真的原子，就可以使用塊操作（比如在一步中將一個原子設為真，其它為假，在它們的聯合馬爾科夫毛毯中取樣）。這樣一個基詞合取式的估計概率就是當馬爾科夫鏈收斂時這些基詞為真的取樣所佔的比例。因為概率分佈往往有多種樣式，我們需要多次執行馬爾科夫鏈。當一個馬爾科夫邏輯網是正規化時，我們可以縮短預處理時間，運用MaxWalkSat這樣一個用於求解加權可滿足性問題的區域性搜尋演算法（比如，找到一個真的賦值使得滿足的規則的權重之和最大）（Kautz et al.，1997）來搜尋模式再執行馬爾科夫鏈。當存在硬約束時（規則的權重無窮大），MaxWalkSat能發現滿足它們的區域，然後我們可再用吉布斯取樣法對這些區域取樣來估算概率。

學習

我們可以從多個關係資料庫中學習馬爾科夫邏輯網的權重（為了簡便下面只討論一個數據庫的情況，一般化到多個數據庫太瑣碎就省略了）。先引入閉型世界假定（Genesereth & Nilsson，1987）：如果一個基本原子不在資料庫中，那我們就假定它為假。如果有n個基本原子，那麼資料庫最有效是向量形式x=（x1,…,xl,…,xn），xl是第l個基本原子的值（如果在資料庫中為1，否則等於0）。有了資料庫，原則上馬爾科夫邏輯網的權重可以使用標準的方法學習到，如下：如果第i個規則在資料x中有ni(x)個真的基本形，那麼等式3的對數概似函式對權重wi的導數為

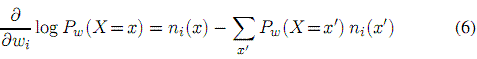
其中的求和是對所有事件庫x‘，而Pw（X=x’）是P（X=x’）用當前的權重向量w = （w1,…,wi,…）計算的。換句話說，第i部分的斜率就是它為真的基本形式與數學期望的差。不幸的是，即使一個簡單規則要數它的基本形式數量也是很棘手的事，如下（Dan Suciu）。

命題6.1 對一個一階邏輯規則的真基本形計數是一個和它長度相關的#P-complete難題。

證明：計數滿足單調二元合取正規化命題的賦值數是個#P-complete難題（Roth，1996）。這個問題可簡化為如下的計數一個知識庫的一條一階邏輯規則的真基本形問題，設一個知識庫由R（0，1）、R（1，0）、R（1，1）基本原子組成，有一個單調二元合取正規化規則Ф由謂詞R（xi，xj）的合取式組成，而謂詞如xi∨xj（比如（x1∨x2）∧（x3∨x4）為R（x1，x2）∧R（x3，x4））。這樣滿足二元正規化的賦值與Ф為真的基本形之間有一一對應關係。（證畢）

在大領域一條規則的真基本形數量可以估算，通過均勻取樣並檢查是否為真來實現。在小的領域，如下面我們的實驗一樣，我們使用一種有效的遞迴演算法來得到精確的數量。

等式6的另一個問題是計算為真的基本形的數學期望值同樣棘手，需要對整個模型進行推算。另外，高效的優化方法還需要計算對數似然（等式3）和配分函式Z，這可以使用蒙特卡洛最大似然估計法（MC-MLE）（Geyer & Thompson，1992）。可以，在我們的實驗中是使用吉布斯取樣法來計算蒙特卡洛最大似然值，微分在合理時間內往往還沒有收斂，而使用沒有收斂的鏈來取樣往往得不到好的結果。

在空間統計、社會網路建模、語言處理等領域廣泛使用的一種更有效的選擇是優化擬似然方法（Besag，1975）

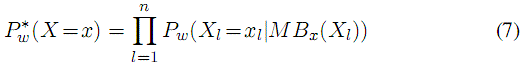
MBx（Xl）是Xl的馬爾科夫毛毯的狀態。擬對數似然的微分是

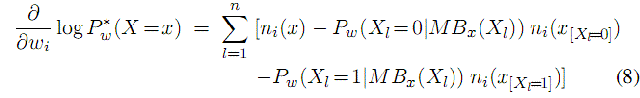
其中ni(x[xl=0])是當我們強制xl=0同時其餘不變的情況下第i條規則為真的基本形數量，ni(x[xl=1])也同樣。計算這個表示式（或者等式7）不需要對整個模型進行推測。我們還用有限記憶空間的BFGS演算法對對數擬似然法進行優化（Liu & Nocedal，1989），使得計算在下面幾個方面更高效：

­ 忽略第i條規則中不出現的謂詞，等式8的求和速度大大加快；
­ ni(x)、ni(x[xl=0])、ni(x[xl=1])不隨權重變化，只需要計算一次；
­ 因為ni(x)=ni(x[xl=0])=ni(x[xl=1])，只改變一個基詞的值不會改變基本規則的真假，因此可以忽略。特別的對任何有至少兩個為真的基詞的句子也成立，這往往是絕大多數基本規則的特性。
為了避免過度擬合，我們先針對每個權重利用高斯法對擬似然方法進行了變形。

可以使用歸納邏輯程式設計技術來精煉已有或者學習新增的規則，甚至從頭學習一個馬爾科夫邏輯網。為此，我們使用了CLAUDIEN系統（De Raedt & Dehaspe，1997）。和其它只學習霍恩子句的歸納邏輯系統不同，CLAUDIEN能學習任意的一階邏輯句子，因此非常適用於馬爾科夫邏輯網，還可通過設定特別語言偏好使用CLAUDIEN來精煉馬爾科夫邏輯網的結構。下一步我們計劃象MACCENT解決分類問題（Dehaspe，1997）一樣，將象Della Pietra et al發明的技術或方法等一般化到一階邏輯領域，將結構學習功能完全引入到馬爾科夫邏輯網中。

實驗

我們用描述華盛頓大學電腦科學工程系的知識庫來測試馬爾科夫邏輯網。該領域由12個謂詞、10大類2707個常陣列成，型別有：出版物（342個常數）、人物（442）、課程（172）、專案（153）、學期（20）等等；謂詞有：Professor(person)、Student(person)、Area(x, area)（x可以取出版物、人物、課程和專案的值)、AuthorOf(publication,person)、 AdvisedBy(person,person)、YearsInProgram(person,years)、CourseLevel(course, level)、TaughtBy(course,person,quarter)、 TeachingAssistant(course,person,quarter)等等；另外還有10個等於謂詞：SamePerson(person,person)、 SameCourse(course, course)等等，如果兩個引數值代表相同的常數，那麼就為真。

使用變數型別後，所有可能的基本原子（第六章的n）總數為4106841，而資料庫含有3380個元組（比如3380個為真的基本原子）。我們通過抓取系網站的網頁(www.cs.washington.edu)獲取資料，出版物和作者之間的關係通過BibServ資料庫（www.bibserv.org）所有記錄中的作者欄位至少含兩部分（名、姓）獲得。

四個自願者每個人都提供了一套一階邏輯規則來描述這個領域，為我們建立了知識庫（這些自願者不知道資料庫中的元組，但他們都是系裡的成員，對整個繫有一定的瞭解）。整合起來後我們獲得了一個有96條規則的知識庫。整個知識庫、資料、演算法的引數、自願者的指示在http://www.cs.washington.edu/ai/mln可以找到。知識庫中有類似這樣的規則：學生不是教授；每個學生至少有一個導師；如果一個學生是一篇論文的作者，那麼他的導師也是；研究生只上他導師的課程；一篇出版物的作者至少有一位是教授；物理博士第一階段的學生沒有導師等等。請注意上述規則並不總是正確的，但通常是。

為方便訓練和測試，我們按人工智慧、影象、程式語言、系統和理論5個領域將資料庫分成5個子資料庫。教授和課程這些常數被手工分配到各個領域，其它常數被賦予它們最常出現的領域，然後元組被新增到其中常數所屬的領域，含有不同領域常數的元組被刪除以避免訓練測試混亂。這些子資料庫平均在58457個可能的基本原子中有521個真的基本原子。

我們使用了一個留下一個的測試策略，每次測試一個領域時採用其餘四個領域的訓練結果。兩個測試任務是預測謂詞AdvisedBy（x，y）：任務A，其它資訊都知道；任務B，除了Student(x) 和Professor(x)以外，其它資訊都知道。在兩個例子中我們都測量了所有領域中謂詞AdvisedBy（x，y）的基本形的平均條件對數似然率，畫出查準率查全率曲線，然後計算曲線下的面積。這項任務就是連線預測的一個例項，這個問題在統計關係學習（見第8章）中廣泛關注。測試中所有知識庫被轉化成正規化，時間結果是基於2.8G赫茲奔4處理器的主機。

1. 測試的系統

   為了評估使用邏輯和概率推理的馬爾科夫邏輯網，我們計劃將它與純邏輯法和純概率方法相比較，同時我們還對使用歸納邏輯程式技術的規則自動歸納感興趣。下面各小節詳細描述了用於比較的各類系統。

1.1 邏輯

使用純邏輯實驗的主要目的是為了幫助我們回答一個重要問題，那就是將概率引入邏輯知識庫是否能夠提升我們對某領域建模的能力。為了做到這一點需要我們在回答問題時僅使用邏輯推理，但實際上這非常複雜，因為計算對數似然率和查準率查全率曲線下的面積需要概率，或者至少對測試中為真的每個基本原子要有“確信度”的衡量值。為此，我們使用了以下方法來近似，設KB為一知識庫，E為已證實的原子集合，XKB∪E為滿足KB∪E的事件集，那麼，我們查詢的原子q的概率為P(q)=|XKB∪E∪q|/|XKB∪E|，這是q在XKB∪E為真的比例。

一個更嚴重的問題是知識庫可能不一致（從自願者收集的知識庫更是如此），這時P(q)公式的分母為0（設想一下一個不一致的知識庫可能包含任意規則）。為了解決這個問題，我們重新將XKB∪E定義為滿足最大可能基本規則數量的事件集合，再用吉布斯取樣法對這個集合進行取樣，每次鏈的初始狀態由WalkSat方法來獲得。每一步吉布斯取樣都有概率：如果新狀態滿足的規則大於當前狀態，那麼，概率為1（也就是當前狀態的概率應該為0）；如果滿足的規則數量與當前狀態相等，則概率等於0.5；如果新狀態滿足的規則數量要少則概率為0。然後我們再用最大滿足的規則來計算概率。實際上，等同於從知識庫中構建一個權重無窮大的馬爾科夫邏輯網。

1.2 概率

另外一個需要實驗來幫我們回答的問題是是否已經存在足夠強大的（命題）概率模型而不再需要馬爾科夫邏輯網的表達能力。 為了應用這種模型，這個領域需要定義一些有表現力的屬性值來命題化，在這種高度關聯的領域中建立好的屬性對於命題學習者來說非常困難。無論如何，在平衡了更多潛在關係資訊表達能力和極其冗長的屬性向量後，我們定義了兩套命題屬性：order-1和order-2。前者包含了查詢謂詞中個體常數的特性，後者包含了常數之間關係的特性。

對於order-1的屬性，我們為每對（a，b）定義一個變數，a是詢問謂詞的一個自變數；b是某個謂詞的自變數，它的值和a一樣。我們定義的變數代表這個謂詞為真的基本形的比例。例如AdvisedBy（Matt，Pedro）有：Pedro是否是學生，Pedro的出版物佔比，Matt當助教的課程佔比等等。

order-2屬性是這樣定義的：給定詢問謂詞Q（q1,q2,…,qk），考慮所有k個謂詞和k個常數q1,q2,…,qk一一對應集合集，例如Q是AdvisedBy（Matt，Pedro）那麼{TeachingAssistant（-，Matt，-），TaughtBy（-，Pedro，-）}是其中一個集合，這個例子就有2K個屬性，每個對應於k個謂詞的某個為真的基本形。屬性的值等於訓練中當未賦值的變數被賦予相同的值時，謂詞集有特定真賦值的次數。例如，上述變數為“CSE546”和“Autumn0304”，集合{TeachingAssistant（CSE546，Matt，Autumn0304），TaughtBy（CSE546，Pedro，Autumn0304）}在訓練時有一些為真的賦值（比如，{True，True}，{True，False}……）,屬性值就是滿足{True，True}為真賦值的常數集數量；{True，False}也一樣；以此類推。查詢謂詞AdvisedBy（Matt，Pedro）的order-2屬性舉例有：Pedro教的課程中Matt任助教的頻度（反過來不任助教的頻度），有多少出版物是Matt和Pedro一起寫的，等等。

最後得到的28個order-1屬性和120個order-2屬性（任務A）通過訓練學習被我們分散到5個等頻度的桶中，我們使用了兩種命題學習方法：簡單貝葉斯（Domingo & Pazzani，1997）和貝葉斯網路（Heckerman等，1995）（每個節點最大4個父節點，結構和引數使用VFBN2演算法（Hulten & Domingos，2002）求得）。order-2屬效能幫助簡單貝葉斯分類，但是降低了貝葉斯網路分類的效能，因此我們報告簡單貝葉斯結果時使用order-1和order-2屬性，而貝葉斯網路僅僅用order-1屬性。

1.3 歸納邏輯程式

我們起始的知識庫是自願者提供的，但是我們對能否用歸納邏輯程式方法自動得到也感興趣。前面提到過，我們使用CLAUDIEN方法從資料中歸納知識，CLAUDIEN是這樣執行的：本地範圍、最小精度0.1、使用最小覆蓋、最大複雜度10、廣度優先搜尋。CLAUDIEN的搜尋空間由它的語言偏好決定，我們架構這樣的語言偏好以允許：一個句子最多3個變數；一個句子中謂詞數量不限；一個句子中一個謂詞至多以二次肯定形式出現和二次否定；謂詞的自變數有型別。為了最小化搜尋，改善結果，我們不使用等於謂詞（如SamePerson）。

除了從訓練資料中歸納規則，我們還對自動優化由自願者提供的知識庫感興趣。CLAUDIEN本身沒有這個功能，但可以構建一個語言偏好來模擬，對於知識庫的每個規則我們允許CLAUDIEN這樣做：（1）移除任意數量的詞；（2）增加至多v個新變數；（3）增加至多l個新詞。我們在一臺Sun-Blade 1000主機上對集合{（1，2），（2，3），（3，4）}的每對（v，l）執行CLAUDIEN24小時，三個結果都很相近，我們報告了（3，4）的結果。

1.4 馬爾科夫邏輯網

我們要將上述系統與馬爾科夫邏輯網比較。這些馬爾科夫邏輯網使用均值為0、方差為1的高斯分佈的權重來訓練，初始權重都設為0。為了優化，我們使用的L-BFGS的Fortran版本（Zhu等 1997和Byrd等 1995），所有引數都是預設值，收斂精度為10-5。用第5章描述的吉布斯取樣法來進行推理，10個馬爾科夫鏈並行，馬爾科夫鏈的初始狀態由MaxWalkSat確定。吉布斯取樣步數由DeGroot和Schervish的準則（2002，pp.707和740-741）來決定，取樣一直要進行到我們有95%的確信度，也就是說在95%的節點中真值的偏差在1%之內（忽略一直為真或假的節點），取樣的最小步數和最大步數分別為1000和500000，每步一次取樣。通常，推理會在5000-10000步間收斂。結果對設定的收斂精度不敏感。

2. 結果

2.1 用MC-MLE來訓練

最初我們使用蒙特卡洛最大似然法來訓練馬爾科夫邏輯網，用了10個吉布斯鏈，初始狀態與相應一階邏輯謂詞為真的概率對應。因為每步僅少許滿足的句子需要改變，吉布斯取樣每一步執行得很快，在華盛頓大學電腦科學工程系這個例子上，我們的應用每步約4-5毫秒。我們用最大穿越所有謂詞的Gelman R準則（Gilks等，1996）來判斷這些鏈是否達到它們的平穩分佈。因為直覺告訴我們，大多數原子總是假的，對它們重複取樣沒什麼效率，所以，為了加速收斂，我們在吉布斯取樣中優先採樣在資料中或初始狀態中為真的原子，這樣在均勻選擇原子基礎上可以提高收斂速度大約一個數量級。儘管進行了這些優化，吉布斯取樣法還是花過分長的時間來達到一個合理的收斂門限（比如，R=1.01）。在運行了24小時後（大約每鏈2百萬步吉布斯取樣），所有訓練集的R值平均為3.04，沒有一個訓練集R值低於2（除了在開始階段短暫地接近1.5外）。我們估計將花費20至400天來完成R值為2.0這樣一個弱收斂門限的訓練，因此必須考慮使用象L-BFGS這樣迭代以尋找最小值。如果我們忽視收斂門限和縮短訓練時間到小於10個小時，實驗證明得到的模型會很差。只有有了象Swendsen-Wang演算法（Edwards & Sokal，1988）這樣的MCMC改進技術，加上能更好地選擇初始狀態和近似計數，MC-MLE才會實用，用它的目前版本來訓練不太可行。（注意：在學習過程中MCMC是對整個基網運算的，太大了無法應用MaxWalkSat）

2.2 用擬似然來訓練

和MC-MLE相反，擬似然法訓練相當快。正如第6章討論，一旦初始句子和滿足的基本原子計數完成，訓練的每次迭代可以做得相當快。平均計數時間花費2.5分鐘（5組測試），而每次訓練平均255次L-BFGS迭代，一共16分鐘。

2.3 推理

推理也相當快。在知道全部資訊（x，y）條件下，推算所有AdvisedBy（x，y）概率，人工智慧專業的測試資料（4624個原子）花了3.3分鐘；圖形專業的（3721個原子）花了24.4分鐘；程式設計專業（784）花了1.8分鐘；系統專業（5476）用了10.4分鐘；理論專業（2704）用了1.6分鐘。吉布斯取樣步數範圍在4270-500000之間，平均124000，而每次吉布斯取樣大約18毫秒，每秒200000-500000步。在知道部分資訊條件下，推理的平均時間是14.8分鐘（全部資訊是8.3）。

2.4 比較

我們對比了12個系統：知識庫（KB）、CLAUDIEN（CL）、以知識庫為語言偏好的CLAUDIEN（CLB）、KB+CL、KB+CLB、MLN（KB）、MLN（CL）、MLN（CLB）、MLN（KB+CL）、MLN（KB+CLB）、簡單貝葉斯（NB）和貝葉斯網路學習（BN）。在所有這些系統中我們都對概率使用了加一平滑。

表Ⅳ彙總了這些結果。圖二顯示了所有領域的查準率/查全率曲線（也就是所有AdvisedBy（x，y）原子的平均），圖三至圖七分別顯示了5個領域的查準率/查全率曲線。馬爾科夫邏輯網顯然比其它系統更精確，展示了這種方法的前途。純邏輯和純概率方法常常遭受需推斷中間謂詞的困擾而馬爾科夫邏輯網大都不受影響；簡單貝葉斯在一些測試集計算AUC很好，但在其它集合很差，它計算CLL都一樣差；CLAUDIEN自己都做得不好，加入到馬爾科夫邏輯網的知識庫時也沒什麼提高，使用CLAUDIEN來提煉知識庫在AUC時表現不好，但在算CLL時比用CLAUDIEN白手起家要好；總之，效果最好的邏輯方法是KB+MLN，但實驗結果要比最好的馬爾科夫邏輯網遜色很多。一般來說，在50%查全率左右時查準率急降是因為資料的不完整，因而只能確認一小部分的AdvisedBy關係。檢查顯示在非常低查全率下偶然幾次小的查準率急降是因為學生在共著許多出版物後畢業或者更換了導師。

B4

TU2

TU3

TU4

TU5

TU6

TU7

統計關係學習的任務

許多統計關係學習的任務可以精確地用馬爾科夫邏輯網表達，使得本文所介紹的演算法可以直接得以利用。在本章中，我們將用5個關鍵任務來例證：集合分類、連結預測、基於連結的聚合、社會網路建模和物件識別。

1. 集合分類

   普通分類任務的目標是根據物件的屬性來預測它的類別，集合分類還需考慮相關聯物件的類別（Chakrabarti等（1998），Taskar等（2002），Neville和Jensen（2003））。屬性可以用馬爾科夫邏輯網的謂詞形式A（x，v）表示，其中A代表一個屬性，x表示物件，v是x的A值。每一個類別有一個指派的屬性C，用C（x，v）表示，v是x的類。這樣分類任務就簡單地變為在已知A（x，v）前提下對所有x和v推導C（x，v）是否為真的問題。普通分類可看成在已知A（x，v）前提下對所有xi和xj而言它們的C（xi，v）和C（xj，v）互相獨立的特例。在集合分類中，C（xi，v）的馬爾科夫毛毯含有其它C（xj，v），甚至在已知A（x，v）後也是如此。物件之間的關係可以用謂詞R（xi，xj）表示，顯而易見這還需要再一般化，比方C（xi，v）和C（xj，v）通過間接的還不知道的謂詞互相依賴的，甚至可能還包含了謂詞R（xi，xj）。

2. 連結預測

   連結預測任務的目標就是要在知道物件的屬性和其它可能的關係（Popescul和Ungar（2003））下來判斷兩個感興趣的物件之間是否存在一種關係（比如，安娜是否是鮑勃的物理學博導？）。這個問題的馬爾科夫邏輯網表示形式和集合分類一樣，唯一不同的是推理的目標從C（x，v）變成了感興趣物件間的R（xi，xj）。我們的實驗就是連結預測任務。

3. 基於連結的聚合

   聚合的目標是將相同屬性的物件組合起來。在基於模型的聚合中，我們設產生式P(X)=∑CP©P(X|C)，其中X是物件，C為簇，那麼P(C|X)就是X在簇C中的程度。在基於連結的聚合中，物件以它們之間的連結來聚合（物件關聯越緊密越可能屬於同一個簇）或它們的屬性來聚合（Flake等（2000））。在馬爾科夫邏輯網中，可設一個未觀測謂詞C（x，v）代表x屬於簇v，然後將它和其它觀測到的謂詞加入網中（如R（xi，xj）表示連結、A（x，v）表示屬性）。這樣基於連結的聚合就可通過馬爾科夫邏輯網學習來解決，簇成員的程度由原子C（x，v）的條件概率得出。

4. 社會網路建模

   社會網路就是圖，圖的節點代表社會角色（如人），弧代表它們之間的關係（如友誼）。社會網路分析（Wasserman和Faust，1994）關注於為相關角色的屬性和連結建模。例如，兩個角色之間形成連結的概率依賴於類似的它們屬性；反過來，兩個連結的角色更可能有某些特定的屬性。這些模型都是典型的馬爾科夫邏輯網，能精確地用公式∀ x∀ y∀ v R(x,y) ⇒ （A（x，v）⇔A（y，v）），其中x和y是角色，而這個規則的權重代表了關聯性和屬性類似性之間相關的強度，例如，朋友之間傾向於有相同的吸菸習慣的模型可用規則∀ x∀ y Friend(x,y) ⇒ (Smoke(x) ⇔ Smoke(y))（表1）。馬爾科夫邏輯網不僅能描述先有的簡單的社會網路模型，而且還能描述更復雜的模型（比如用多型別關係和屬性的規則，更復雜的依賴關係等）。

5. 物件識別

   物件識別（記錄關聯、重複刪除等等）需要解決判斷資料庫中記錄是否與現實世界某一實體相同（例如目錄資料庫中哪些代表了同一個出版物）的問題。對許多公