SIFT特徵-尺度不變特徵理解

簡介

SIFT，即尺度不變特徵變換（Scale-invariant feature transform，SIFT），是用於影象處理領域的一種描述。這種描述具有尺度不變性，可在影象中檢測出關鍵點，是一種區域性特徵描述子。該方法於1999年由David Lowe首先發表於計算機視覺國際會議（International Conference on Computer Vision，ICCV），2004年再次經David Lowe整理完善後發表於International journal of computer vision（IJCV）。截止2014年8月，該論文單篇被引次數達25000餘次。

特點

• 對旋轉、尺度縮放、亮度變化保持不變性，對視角變化、噪聲等也存在一定程度的穩定性
• 獨特性，資訊量豐富，適用於在海量特徵資料中進行快速，準確的匹配
• 多量性，即使少數幾個物體也可以產生大量的Sfit特徵向量
• 可擴充套件性，可以很方便的與其他形式的特徵向量進行聯合

高斯影象金字塔

理解

高斯影象金字塔是把原影象先放大一倍（如150✖150到300✖300），對這個放大後的影象進行高斯濾波（之前講過的高斯模糊，可以回去看一下），其中模糊半徑分別取σ、kσ、k^2σ等等，得到若干個模糊後的影象，這是第一組，然後依次按照比例為2縮小影象，如此重複，構建一個有若干組(Octave)的金字塔，每組分為若干層。

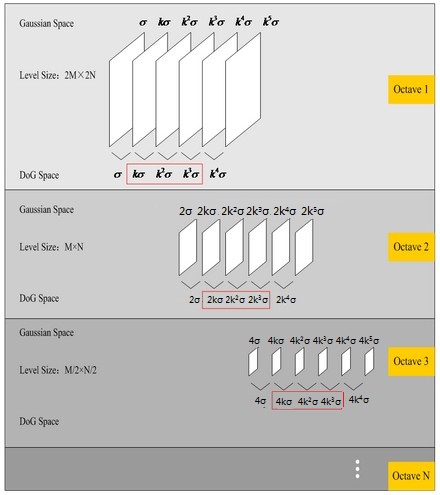
補充

用O表示octave（第幾組）,用L表示layer（第幾層），則（O,L）就代表高斯影象空間中的確定的一副影象。

DOG金字塔

理解

DOG金字塔（Difference of Gaussian）就是高斯金字塔同一octave下相鄰兩層的差分構成的金字塔。

解釋

之所以要構建差分金字塔，就是為了找到在不同尺度和不同模糊程度下的不變特徵，而這正式SIFT要提取的"穩定"特徵。

空間極值點檢測

理解

這裡的空間極值點檢測，其實就是在DOG空間的一個octave下比較每一個畫素和它相鄰點的大小，看它是否比其他點都要大。如果比周圍點都大，說明它是是區域性的極值點（這一點我們可以類比一個二次函式，它的最低點是不是比周圍點都小，所以它是極值點，當然它也恰巧是最低點）。

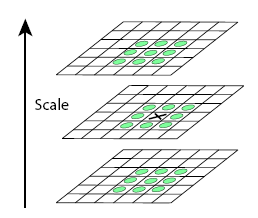
補充

這裡我們要計算圖中打x的點是不是極值點，那麼我們就要比較它與不同層以及同層的周圍一共26個點的大小，才能確定它是不是空間的極值點。

關鍵點精確定位

理解

由於我們上面的操作都是在離散空間操作的，我們知道，離散空間取到的極值點，並不一定是真正的極值點，所以我們需要通過類似函式擬合的方式，對離散點進行擬合使之連續，在連續空間就很容易利用我們的知識求取極值點。

計算

我們將DOG空間的泰勒展開式子看成其擬合函式，就可以操作連續空間的函數了。
候選特徵點x，其偏移量定義為Δx，其對比度為D(x)的絕對值∣D(x)∣，對D(x)應用泰勒展開式

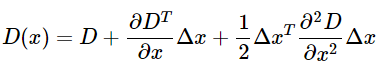
由於x是D(x)的極值點，所以對上式求導並令其為0，得到

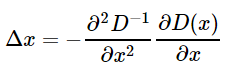
然後再把求得的Δx代入到D(x)的泰勒展開式中

設對比度的閾值為T，若∣D(x^)∣≥T，則該特徵點保留，否則剔除掉。

關鍵方向匹配

理解

上面說了，SIFT特徵具有旋轉不變性，而它的旋轉不變性就在於每一個關鍵點都有一個基準方向，而這個基準方向是由影象的區域性決定和分配的。

計算

梯度的模值和方向定義如下：

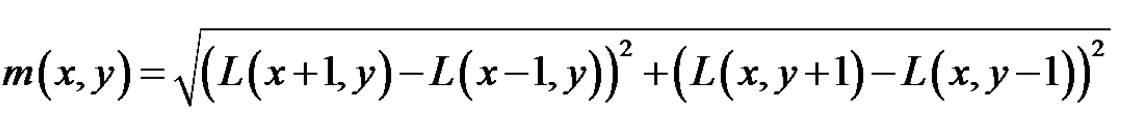
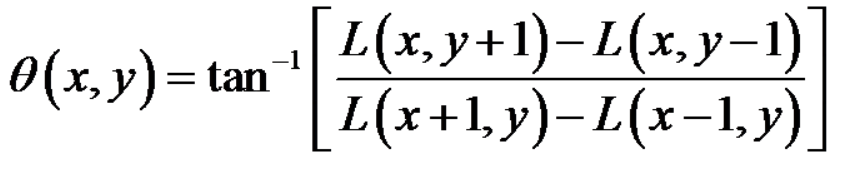
利用這個公式計算以關鍵點為中心的領域內所有點的梯度方向（8個方向），計算完之後，我們使用直方圖來統計領域內畫素的梯度和方向。梯度直方圖將0~360度的方向分為36個立柱，每柱10度。直方圖的峰值代表的是該關鍵點的主方向。為了增強魯棒性，如果由立柱的值大於峰值的80%，我們將其作為關鍵點的輔方向。（下圖只花了8個方向）。

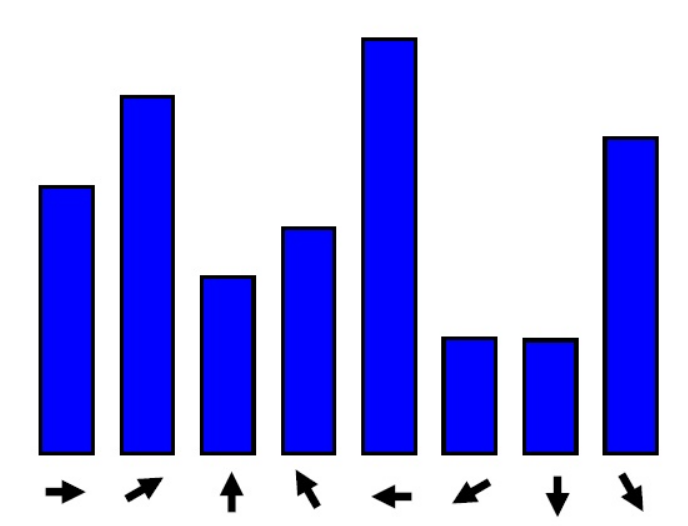
關鍵點描述

理解

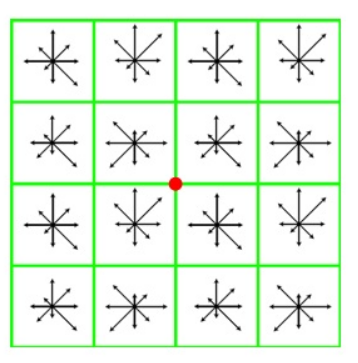
關鍵點描述是對領域內高斯影象直方圖統計結果的一種表示形式，我們找到的特徵點引數有位置、尺度和方向。在關鍵點周圍的領域內，將其分為m✖m個子塊，每個子塊以中間點為原點，分別計算梯度直方圖，生成區域性向量，對該向量進行標準高斯函式加權處理，然後對特徵向量進行歸一化處理。每個關鍵點在下圖中可以產生2✖2✖8維向量作為特徵向量。

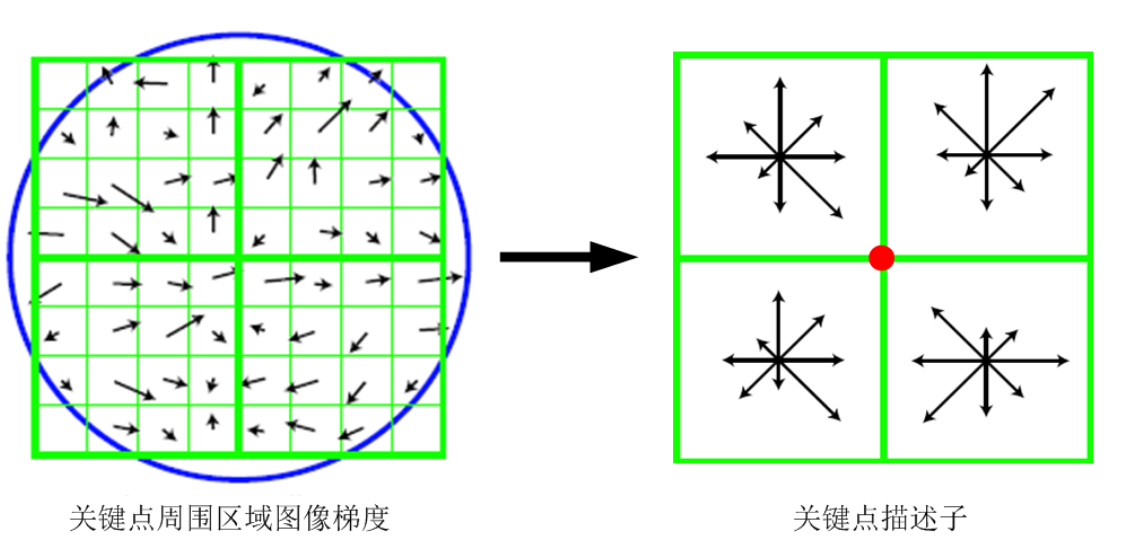
David G.Lowed的實驗結果表明：對每個關鍵點，採用448共128維向量的描述子進項關鍵點表徵，綜合效果最佳：

特徵點匹配

理解

有了目標圖片，對目標圖片計算SIFT特徵，然後用其特徵向量與已知特徵的特徵向量進行歐式距離匹配，其歐式距離越小，匹配度越高。