20172322 《程式設計與資料結構》第九周學習總結
阿新 • • 發佈:2018-11-18
20172322 《程式設計與資料結構》第九周學習總結
教材學習內容總結
本章的內容主要講圖的知識,圖與樹的定義類似,讓樹允許在其每個結點連通多個其他節點,不再有父親孩子之說時就成了圖。圖由頂點和邊構成,頂點一般由A,B,C,D等表示,相應的邊可以表示成(A,B),(B,C)等。圖分為兩種:有向圖和無向圖。
- 無向圖:邊為無序結點的圖。在無向圖中邊(A,B)和邊(B,A)所蘊含的意義是相同的。
- 鄰接的頂點:如果兩個頂點之間有一條邊連通,這兩個頂點就是連通的。
- 完全的無向圖:對於有n個頂點的無向圖來說,如果有n(n-1)/2條邊,該無向圖就是完全的。
- 路徑的長度:路徑是圖中所有的邊的總和,路徑的長度是路徑中邊的條數。
連通的無向圖:如果無向圖中任意兩個頂點之間都存在一條路徑,則認為該無向圖是連通的。
- 環路:首末頂點相同且沒有重邊的路徑。
- 無向樹:連通的、無環無向的圖,其中一個元素被指定為樹根。
- 有向圖:邊為有序結點的圖。在有向圖中邊(A,B)和邊(B,A)所蘊含的意義是不同的。
- 路徑:圖中連通兩個頂點的有向邊序列。
- 拓撲序:在有向圖中,有一條邊從A到B,則把A安排在B之前,這種排列順序成為拓撲序。

- 網路(加權圖):每一條邊都有相應的價值或者代價。
- 圖的遍歷:
- 廣度優先遍歷:類似於樹的層序遍歷,例如:
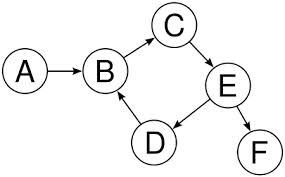
從 A 開始的遍歷順序為(鄰接的遍歷順序為字母升序):ABCEDBF。- 深度優先遍歷:類似於樹的前序遍歷,例如:

- 深度優先遍歷和廣度優先遍歷的唯一不同是:深度優先遍歷使用棧而非佇列來管理遍歷。
- 連通性測試:當且僅當廣度優先遍歷中的頂點數目等於圖中的頂點數目時,該圖才是連通的。

最小生成樹:首先明確生成樹的概念,包含圖的全部頂點和所有邊。最小生成樹,其邊的權重之和小於或等於同一個圖中其他任何一個生成樹。例如,普利姆演算法求最小生成樹:
- 最小路徑的判斷:兩種情況
- 兩個頂點之間的最小邊數。
- 加權圖的最便宜路徑。
圖的實現策略:書上講到了兩種實現策略,鄰接列表和鄰接矩陣,而所謂鄰接指的就是實現圖的兩個相鄰的頂點連線起來。
圖的實現策略
鄰接列表實現
- 首先,讓我們來了解什麼是鄰接列表。鄰接列表:儲存方法跟樹的孩子連結串列示法相類似,是一種順序分配和鏈式分配相結合的儲存結構。如這個表頭結點所對應的頂點存在相鄰頂點,則把相鄰頂點依次存放於表頭結點所指向的單向連結串列中。
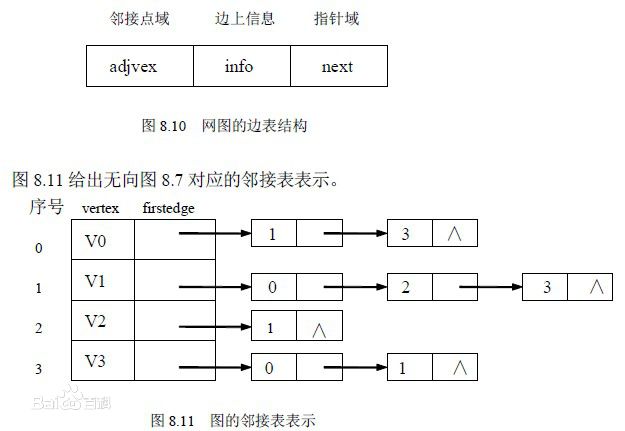
鄰接矩陣實現
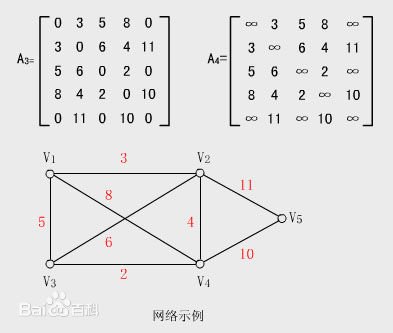
- 鄰接矩陣:利用一個二維陣列實現的矩陣,行列的元素代表頂點,而矩陣中的元素代表邊。
- 在無權圖中,矩陣中的元素為1則代表有邊,而為0時代表無邊。
如圖:
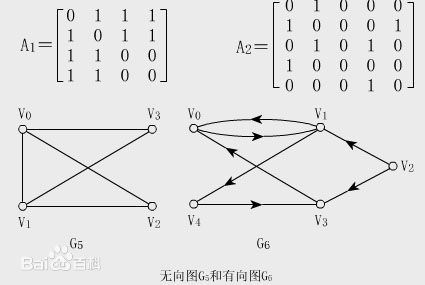
- 在網路中,矩陣中的元素為非0則代表有邊,而為0時代表無邊。
如圖:
教材學習中的問題和解決過程
- 問題一:最先看到書上的鄰接列表時比較懵逼,而且書上所述非常簡單,不知道鄰接列表的結構如何。
- 問題一解決方案:先在網上查閱了部分資料後還是不太明白,僅僅是發現它的結構跟鏈地址法有些類似,但是如何實現的邊不清楚,隨後向王志強老師求助,王老師說的確跟鏈地址法比較類似,但是還有一個更加生動的例子就是糖葫蘆串,每個頂點把與自己相接的頂點列在自己的後面就可以啦。就像這一張圖:

- 問題二:書上關於無向圖的鄰接矩陣實現中是矩陣中的元素如果為一則是連通的,並且是對稱的,那麼對於加權圖來說如何實現?
問題二解決方案:其實這個問題非常簡單,只是自己的腦子沒扭過來,直接把那個1變為需要加上的權重就實現了加權圖。
程式碼除錯中的問題和解決過程
- 問題一:在實現書上的
Graph類補全時遇到一些困難。。 - 問題一解決方案:參考了一些方藝雯同學的程式碼,並且對我自己的程式碼進行了一些優化,例如
isEmpty方法,我原本的程式碼如下:
public boolean isEmpty()
{
if (numVertices == 0)
{
return true;
}
else {
return false;
}
}- 但是方藝雯同學的程式碼是
public boolean isEmpty()
{
return (numVertices == 0)
}自己想了想發現這樣的確會簡單很多。這告訴我們應該多多想想演算法的優化。
程式碼託管“點這裡跳轉到碼雲”

- 這周PP15.7的commit寫錯了,應該是PP15.7而不是PP15.1。
上週考試錯題總結
- 錯題1:Heap sort is O(________).
- A .n
- B .log n
- C .n log n
- D .None of the above
錯題1解析:堆排序的時間複雜度是O(nlogn)
- 錯題2:Heap sort is O(n log n).
- A .True
- B .Flase
錯題2解析:跟上題同理。
結對及互評(待修改)
- 部落格中值得學習的或問題:
- 範雯琪同學的部落格課本上的學習內容總結部分寫得十分詳細,值得學習。
- 每次看到範雯琪同學的部落格自己都比較慚愧,實在是非常優秀,可想而知她在部落格這一方面所做出的努力,我也非常想想她學習。
- 程式碼中值得學習的或問題:
- commit提交的解釋清晰明瞭,我覺得我應該學習。
- 有許多程式碼的問題都是我向她詢問,我很感謝她
點評過的同學部落格和程式碼
- 本週結對學習情況
- 結對學習內容
- 她提醒了我的PP12.1有點問題,感謝。
其他
- 感悟:感覺圖的知識有一些難度,特別是剛剛開始接觸的時候,鄰接列表的知識讓我無從下手。
課本單詞
(本部分用於收集本章節後的生詞)
- graph:圖
- vertice:頂點
- edge:邊
- undirected graph:無向圖
- adjacent:鄰接的
- self-loop:自迴圈
- complete:完全的
- path:路徑
- path length:路徑長度
- connected:連通的
- cycle:環路
- acyclic:無環的
- directed graph:有向圖
- topological order:拓撲序
- network(weighted graph):網路(加權圖)
- breadth-first traversal:寬度優先遍歷
- depth-first traversal:深度優先遍歷
- spanning tree:生成樹
- minimun spanning tree:最小生成樹
- adjacency list:鄰接列表
- adjacency matrix:鄰接矩陣
學習進度條
| 程式碼行數(新增/累積) | 部落格量(新增/累積) | 學習時間(新增/累積) | 重要成長 | |
|---|---|---|---|---|
| 目標 | 5000行 | 30篇 | 400小時 | |
| 第一週 | 0/5000 | 2/2 | 8/8 | 認真學習!積極向上 |
| 第二週 | 812/812 | 1/3 | 22/30 | |
| 第三週 | 814/1626 | 1/4 | 20/50 | |
| 第四周 | 1386/3012 | 2/6 | 20/70 | 愉快的國慶節就要結束了... |
| 第五週 | 1222/3234 | 1/7 | 30/100 | |
| 第六週 | 1327/4561 | 2/7 | 30/100 | 啦啦啦啦啦 |
| 第七週 | 1170/5631 | 1/8 | 33/133 | |
| 第八週 | 1250/6881 | 2/10 | 30/163 | |
| 第九周 | 2275/9156 | 1/11 | 31/194 |
- 改進情況:根據學姐的建議在借鑑程式碼時放上了自己的程式碼並加以說明。
