1、訓練、驗證、測試集的劃分

        在配置訓練、驗證、測試資料集的過程中，通過做出正確的決策可以幫助建立一個高效的神經網路，這些決策包括但不限於：神經網路包含多少層、每層包含多少隱藏單元、學習速率是多少、各層採取哪些啟用函式。

        通常在專案開始時，我們會有一個初步的想法，比如構建一個含有特定層數、隱藏單元以及資料集的神經網路，然後進行編碼，並根據得出的結果來完善自己的想法，改善策略，或者為了找到更好的神經網路不斷迭代更新自己的方案。

        通常情況下，從一個領域或者應用領域積累的直覺經驗，比如從影象處理到自然語言處理，通常無法直接轉移到其他應用領域，最佳決策取決於所擁有的資料量，輸入特徵的數量、

        高質量的訓練集、驗證集和測試集是提高迴圈效率的一種重要的手段。當樣本數量較小時，可以依據6、2、2佔比進行劃分。對於資料量過百萬的應用，訓練集可以佔比99.5%，驗證集和測試集各佔0.25%，或者驗證集0.4%，測試集0.1%。其中測試集設定的目的是為了做出無偏估計，如果不需要無偏估計的話可以不設定測試集。最好保證驗證集和測試集的資料來自同一分佈。

2、偏差和方差

        偏差和方差是兩個易學難精的概念，理解兩者的關鍵資料是訓練集誤差和驗證集誤差。初始模型完成後，首先需要知道演算法的偏差高不高，如果偏差較高，試著評估訓練集或者訓練資料的效能，但如果偏差很高的話，那麼需要做的就是嘗試訓練一個新的神經網路，比如包含更多隱藏層或隱藏單元的網路，或者花費更多的時間來訓練網路，或者嘗試更多的優化演算法。最重要的是需要反覆去嘗試，這個過程可能有用也可能沒用，不過通常情況下采取更大的神經網路都會有所幫助，延長訓練時間不一定有用，但也並沒有什麼壞處。不斷在訓練演算法時嘗試這些方法，至少結果能較好的擬合訓練集資料，這是最低的標準。

        一旦偏差降低到了一個合適的範圍，這時候來看一下方差有沒有問題，評估方差需要用到驗證集的資料，如果方差過高，最好的方法就是採集更多的資料，當然很多情況下實施起來比較的困難，也可以通過正則化來解決過擬合問題。

       需要注意的是：其一，高偏差和高方差是兩種完全不同的情況，故解決方法也可能完全不同，一般通過訓練集和驗證集來確定演算法是否存在高方差或高偏差問題，然後根據結果來嘗試部分方法。其二；注意偏差和方差兩者之間的權衡，只要正則適中，那麼構建一個更大的網路便可以在不影響方差的同時減少偏差，而採用更多的資料可以在不影響偏差的同時降低方差。

3、正則化

       深度學習中存在的過擬合問題，一般有兩種解決方法，一種是增加資料量，另一種是更為簡便的方法——正則化。為什麼正則化可以減少過擬合呢？直觀上理解就是如果正則化係數設定的足夠大，權重矩陣W會被設定為接近於0的值，即把多個隱藏單元的權重設為0，基本消除了這些隱藏單元的許多影響。該情況下，這個被大大簡化了的神經網路就會變成一個很小的網路，小到如同一個邏輯迴歸單元，但是深度卻很大，它會使這個網路從過度擬合的狀態更接近高偏差狀態。正則化係數從零到足夠大之間會存在一箇中間值，使得模型處在“剛剛好”的狀態。增大lamda的過程就是減小神經網路所有隱藏單元的過程，使得神經網路變得相對更簡單了。

常用的正則化有：

• L2正則化：缺點是需要嘗試大量的正則化係數的值，計算代價太高；
• dropout正則化（即隨機失活，主要應用在計算機視覺領域，其最大的缺點就是代價函式J不再被明確定義，每次迭代，都會隨機移除一些節點，如果想檢查梯度下降的效能，實際上是很難進行復查的）；
• 資料擴增：對原始圖片進行隨機翻轉、隨意放大後剪裁等；
• Early stopping：即在執行梯度下降時，對訓練誤差進行視覺化在合適的地方停止梯度下降，或者只繪製代價函式J的優化過程，缺點是不能夠獨立的來進行這個過程，因為提早停止了梯度下降也就停止了優化代價函式，優點是隻需要進行一次梯度下降就可以找出w較小值、中間值和較大值，效率比較高；

4、歸一化

       訓練神經網路，其中一個加速訓練的方法就是歸一化，即零化均值、歸一標準差，服從標準正態分佈。可以加速梯度下降演算法。

5、梯度消失和梯度爆炸

       訓練神經網路，尤其是深度神經網路時所面臨的一個問題就是梯度消失或者梯度爆炸，即訓練神經網路時，導數或坡度有時會變得非常大，或非常小，甚至於指數方式變小，增大訓練的難度。

       初始權重設定的比單位矩陣略大或者略小，深度神經網路的啟用函式就會呈爆炸式變化，其值就會變得極大或極小，從而導致訓練難度上升，尤其是梯度指數很小的時候，梯度下降演算法的步長會非常非常小，大大增加訓練花費的時間。

       一個解決的方法是針對不同的啟用函式設定不同的初始權重，比如Relu函式方差設為2/n就比較好。

6、梯度檢驗

       梯度檢驗的目的是為了保證backprop的正確實施，因為實際操作中很難保證backprop每一步都是100%正確的。

在執行梯度檢驗時，使用雙邊誤差會比較好，因為它比單邊誤差更為精確，即:

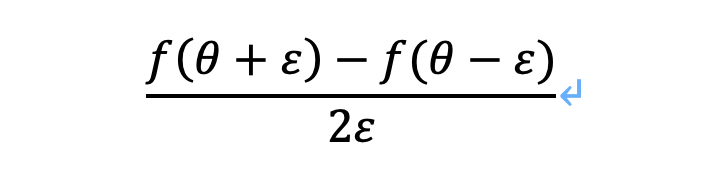
6.1 梯度檢驗的具體步驟：

• 首先將所有引數w1和b1……wL和bL轉換成一個巨大的向量資料，即把矩陣W轉換成一個向量之後做連線運算得到一個巨型向量Θ，由於代價函式J是所有w和b的函式，故現在得到一個關於引數Θ的代價函式J(Θ)。
• 接著同樣可以把dw1和db1……dwL和dbL初始化成大向量dΘ，它與Θ具有相同的維度。

利用上面的雙邊誤差計算公式計算誤差，正常情況下它應該逼近J(Θ)對Θ的偏導數，通過判斷這些向量是否彼此接近來進行梯度檢驗，其中：

• 通過計算兩者的歐式距離（誤差的平方和再求平方根），如果最後得到的ε為10-7或者更小，說明導數逼近很有可能是正確的，因為其值很小；如果為10-5，則需要引起注意，也許沒有問題，也許有bug；如果為10-3，則需要進一步通過除錯來檢驗。

6.2 梯度檢驗中的注意事項

• 不要在訓練中執行它，僅僅將其應用於除錯；
• 如果演算法的梯度檢驗失敗，要檢查所有項，檢查每一項，並試著找出bug，即查詢不同的i值，看看是哪一項導致了兩者的差距變大的；
• 如果代價函式中包含了正則項，記得一定不能忽略；
• 梯度檢驗不能與dropout共同使用，因為每次的迭代過程中，dropout會隨機消除隱藏層單元的不同子集，難以計算代價函式；
• 最後一點比較微妙，現實中可能並不存在這種情況。在w和b接近0的時候，梯度下降的實施是正確的，但在執行梯度下降時，w和b會變得更大，會變得越來越不準確，一種比較少見的做法是在初始化訓練過程中，執行梯度檢驗，從而解決w和b一段時間後遠離0的問題，迴圈反覆這個過程。