降維與度量學習
阿新 • • 發佈:2018-11-19
- 度量學習指距離度量學習,是通過特徵變換得到特徵子空間,通過使用度量學習,讓類似的目標距離更近,不同的目標距離更遠.
- 也就是說,度量學習需要得到目標的某些核心特徵(特點)。比如區分兩個人,2隻眼睛1個鼻子-這是共性,柳葉彎眉櫻桃口-這是特點。
- 度量學習分為兩種,一種是基於監督學習的,另外一種是基於非監督學習的。
1.KNN
有監督學習
工作機制
給定測試樣本,基於某種距離度量找出訓練集中與其最靠近的k個訓練樣本,然後基於這k個“鄰居”的資訊進行預測。
(分類中用投票法,迴歸中用平均法,還可以基於距離遠近進行加權投票或平均。)
注意:KNN沒有顯示的訓練過程,它是“懶惰學習
錯誤率
KNN錯誤率的上下界在1-2倍貝葉斯決策方法的錯誤率範圍內
以最近鄰分類器(K=1)在二分類問題為例:
令
表示貝葉斯最優分類器的結果。給定測試樣本x,若其最近鄰樣本為z,則1NN出錯的概率為x與z類標不同的概率:
2.主成分分析
無監督學習
主成分分析通過正交變換將一組可能存在相關性的變數轉換為一組線性不相關的變數,轉換後的這組變數叫主成分。
模型表示
設投影矩陣為W,樣本點
在新空間超平面上的投影是
。我們希望所有樣本點的投影能夠儘可能地分開,所以目標是使得投影后樣本點的方差最大化。
模型求解
等式條件下求解最優問題用拉格朗日乘子法,得:
於是,只需要對協方差矩陣
進行特徵值分解,將特徵值降序排序,前d個特徵值所對應的特徵向量即為投影矩陣W。
3.因子分析
模型表示

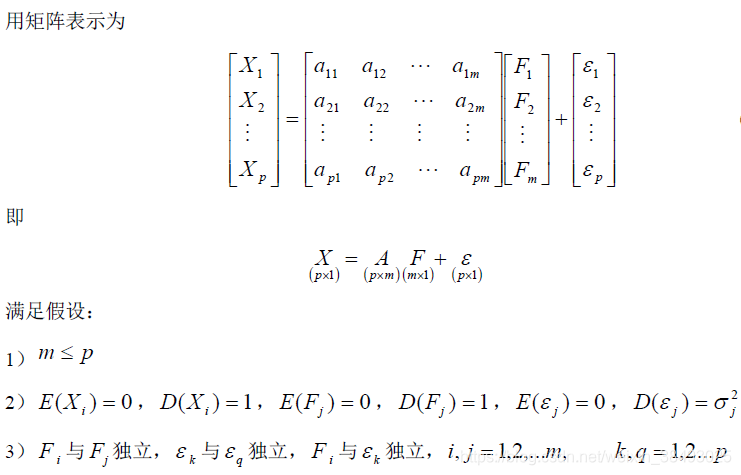
變數意義
- 因子載荷 :反映了第i 個變數在第j個公共因子上的相對重要性。
- 變數 的共同度 :是 方差的主要部分,共同度越大說明公共因子包含 的變異資訊越多。
- 公共因子 對X的方差貢獻 :方差貢獻越大,則該公共因子越重要。
計算步驟
第一步:將原始資料標準化。
第二步:建立變數的相關係數R。
第三步:求R 的特徵根及其相應的單位特徵向量。
第四步:對因子載荷矩陣施行最大正交旋轉。
第五步:計算因子得分。
