1.流形學習的概念

流形學習方法(Manifold Learning)，簡稱流形學習，自2000年在著名的科學雜誌《Science》被首次提出以來，已成為資訊科學領域的研究熱點。在理論和應用上，流形學習方法都具有重要的研究意義。

假設資料是均勻取樣於一個高維歐氏空間中的低維流形，流形學習就是從高維取樣資料中恢復低維流形結構，即找到高維空間中的低維流形，並求出相應的嵌入對映，以實現維數約簡或者資料視覺化。它是從觀測到的現象中去尋找事物的本質，找到產生資料的內在規律。

以上選自百度百科

簡單地理解，流形學習方法可以用來對高維資料降維，如果將維度降到2維或3維，我們就能將原始資料視覺化，從而對資料的分佈有直觀的瞭解，發現一些可能存在的規律。

2.流形學習的分類

可以將流形學習方法分為線性的和非線性的兩種，線性的流形學習方法如我們熟知的主成份分析（PCA），非線性的流形學習方法如等距對映（Isomap）、拉普拉斯特徵對映（Laplacian eigenmaps，LE）、區域性線性嵌入(Locally-linear embedding，LLE)。

當然，流形學習方法不止這些，因學識尚淺，在此我就不展開了，對於它們的原理，也不是一篇文章就能說明白的。對各種流形學習方法的介紹，網上有一篇不錯的讀物（原作已找不到）： 流形學習 (Manifold Learning)

3.高維資料降維與視覺化

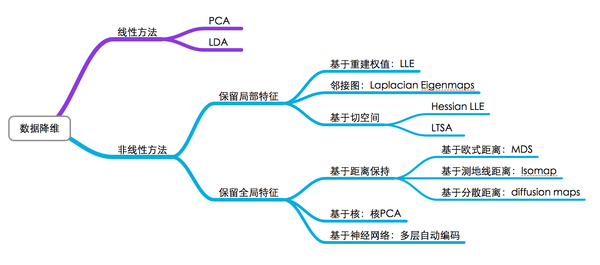
對於資料降維，有一張圖片總結得很好（同樣，我不知道原始出處）：

圖中基本上包括了大多數流形學習方法，不過這裡面沒有t-SNE,相比於其他演算法，t-SNE算是比較新的一種方法，也是效果比較好的一種方法。t-SNE是深度學習大牛Hinton和lvdmaaten（他的弟子？）在2008年提出的，lvdmaaten對t-SNE有個主頁介紹：tsne,包括論文以及各種程式語言的實現。

接下來是一個小實驗，對MNIST資料集降維和視覺化，採用了十多種演算法，演算法在sklearn裡都已整合，畫圖工具採用matplotlib。大部分實驗內容都是參考sklearn這裡的example，稍微做了些修改。

Matlab使用者可以使用lvdmaaten提供的工具箱:

- 載入資料

MNIST資料從sklearn整合的datasets模組獲取，程式碼如下，為了後面觀察起來更明顯，我這裡只選取n_class=5，也就是0～4這5種digits。每張圖片的大小是8*8，展開後就是64維。

digits = datasets.load_digits(n_class=5)
X = digits.data
y = digits.target
print X.shape
n_img_per_row = 20
img = np.zeros((10 * n_img_per_row, 10 * n_img_per_row))
for i in range(n_img_per_row):
    ix = 10 * i + 1
    for j in range(n_img_per_row):
        iy = 10 * j + 1
        img[ix:ix + 8, iy:iy + 8] = X[i * n_img_per_row + j].reshape((8, 8))
plt.imshow(img, cmap=plt.cm.binary)
plt.title('A selection from the 64-dimensional digits dataset')

執行程式碼，獲得X的大小是(901,64)，也就是901個樣本。下圖顯示了部分樣本：

- 降維

以t-SNE為例子，程式碼如下，n_components設定為3，也就是將64維降到3維，init設定embedding的初始化方式，可選random或者pca，這裡用pca，比起random init會更stable一些。

print("Computing t-SNE embedding")
tsne = manifold.TSNE(n_components=3, init='pca', random_state=0)
t0 = time()
X_tsne = tsne.fit_transform(X)
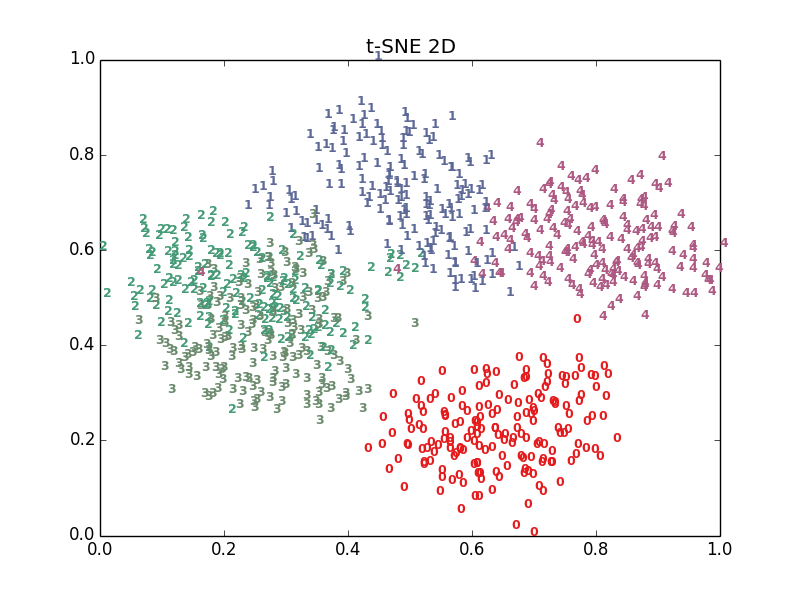
plot_embedding_2d(X_tsne[:,0:2],"t-SNE 2D")
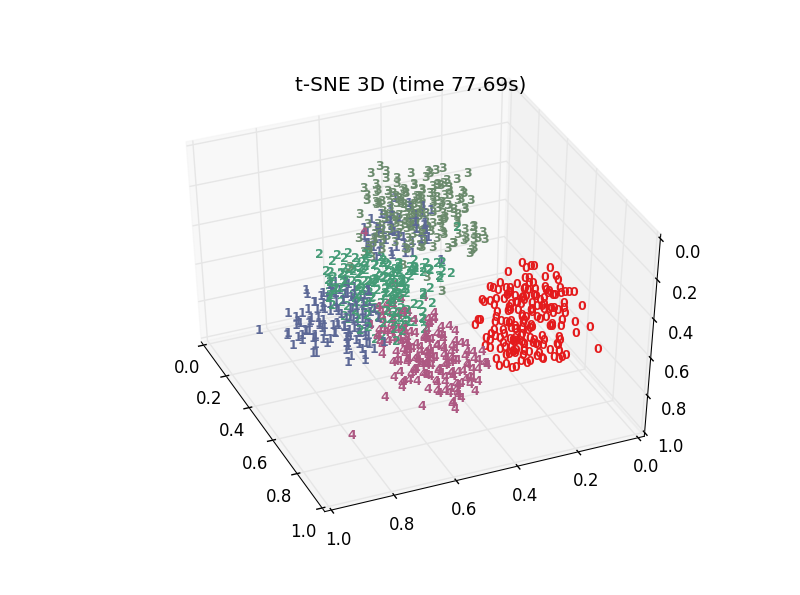
plot_embedding_3d(X_tsne,"t-SNE 3D (time %.2fs)" %(time() - t0))

降維後得到X_ tsne，大小是(901,3)，plot_ embedding_ 2d()將前2維資料視覺化，plot_ embedding_ 3d()將3維資料視覺化。

函式plot_ embedding_ 3d定義如下：

def plot_embedding_3d(X, title=None):
    #座標縮放到[0,1]區間
    x_min, x_max = np.min(X,axis=0), np.max(X,axis=0)
    X = (X - x_min) / (x_max - x_min)
    #降維後的座標為（X[i, 0], X[i, 1],X[i,2]），在該位置畫出對應的digits
    fig = plt.figure()
    ax = fig.add_subplot(1, 1, 1, projection='3d')
    for i in range(X.shape[0]):
        ax.text(X[i, 0], X[i, 1], X[i,2],str(digits.target[i]),
                 color=plt.cm.Set1(y[i] / 10.),
                 fontdict={'weight': 'bold', 'size': 9})
    if title is not None:
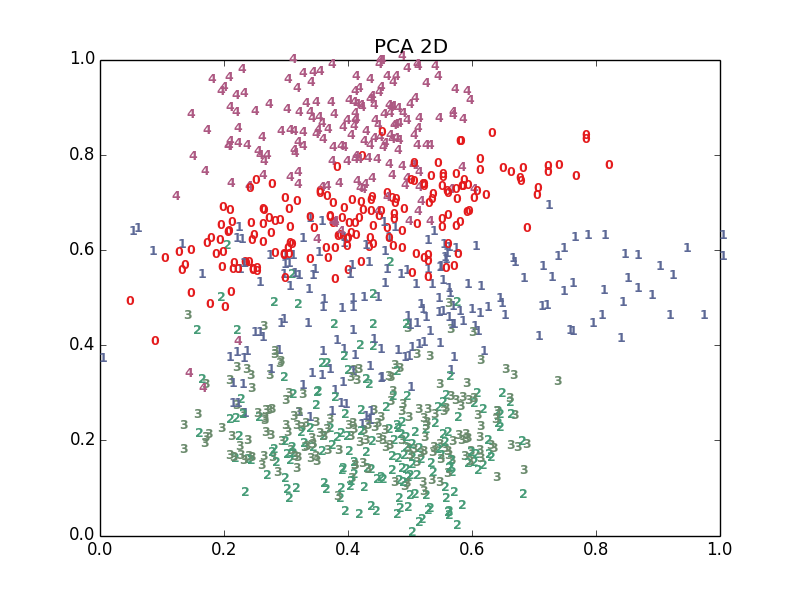
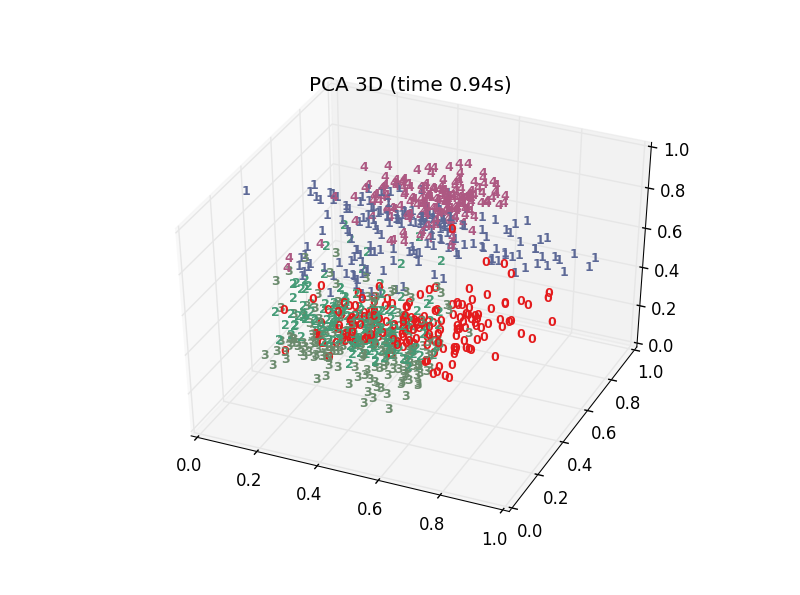
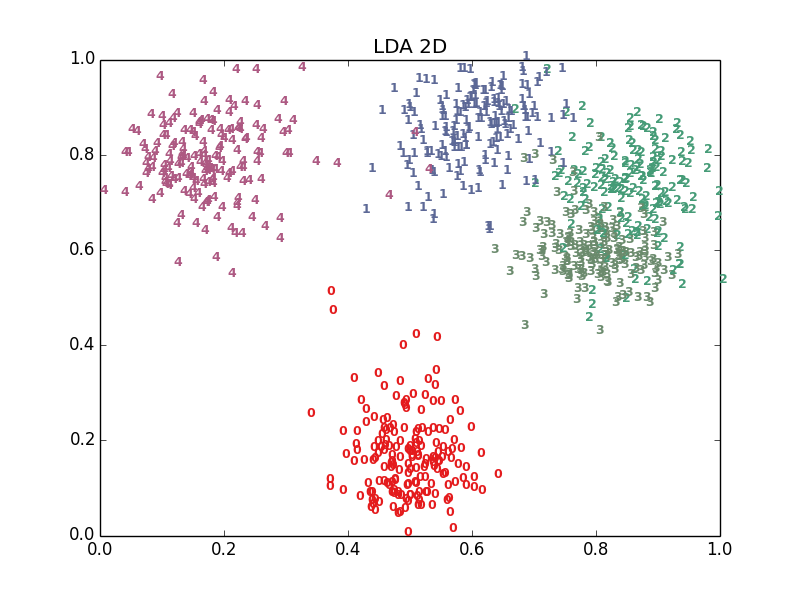
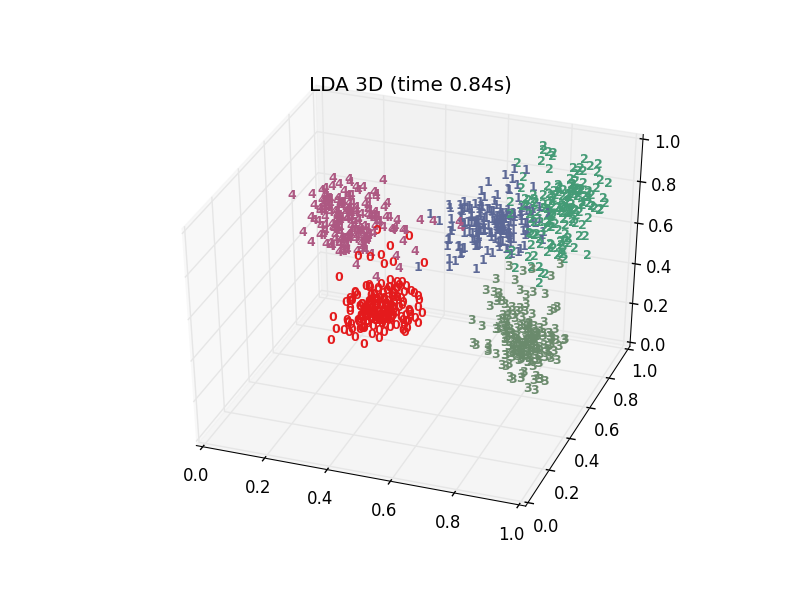
        plt.title(title)

- 看看效果

十多種演算法，結果各有好壞，總體上t-SNE表現最優，但它的計算複雜度也是最高的。下面給出PCA、LDA、t-SNE的結果:

- 程式碼獲取