【 ML 】 Gauss – Newton Iteration Procedure of TOA - Based Positioning Simulation
阿新 • • 發佈:2018-11-22
Gauss – Newton algorithms are:
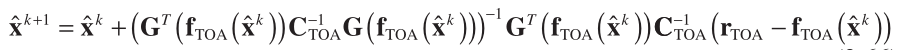 (1)
(1)
where is the Jacobian matrix of
computed at
and has the following expression:
 (2)
(2)
Jacobian matrix is presented in Matlab:
function G = jacob(X, x) % Jacobian matrix computation % -------------------------------- % G = jacobian(X, x) % G = Jacobian matrix % x = 2D position estimate % X = matrix for receiver positions % [dim,L] = size(X); % L is number of receivers; dim is dimension of space f_TOA = sqrt(sum((ones(L,1)*x'-X').^2,2)); G = (ones(L,1)*x' - X')./(f_TOA*ones(1,dim));
使用Gauss-Newton演算法的定位示意圖如下:

可見,真實位置和估計出來的位置大致重合。這說明能定位的同時又有定位誤差,這是很正常的,我們需要關注的是誤差的大小,能否滿足我們的需求:

從上圖可以看出,信噪比為20dB時的均方根誤差為727m,信噪比為30dB時的均方根誤差為216m。
可見,這個誤差無論和ML方法中的牛頓——拉夫森方法以及和NLS方法中的三種方法相比,定位誤差都相差無幾。
相關程式碼就不太方便直接貼出來了,因為有些人是不懂感恩的,拿了你的分享還反咬你一口。
