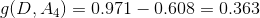機器學習實戰——1.2決策樹(1)
宣告:參考書目《機器學習實戰》作者: Peter Harrington 出版社: 人民郵電出版社 譯者: 李銳 / 李鵬 / 曲亞東 / 王斌
宣告:參考書目《統計學習方法》作者: 李航 出版社: 清華大學出版社 ISBN: 9787302275954
宣告:參考書目《機器學習》作者: 周志華 出版社: 清華大學出版社 ISBN: 9787302423287
參考部落格 Jack-Cui 作者個人網站:http://cuijiahua.com/
目錄
一決策樹
決策樹(decision tree)是一種基本的分類與迴歸方法。在分類問題中,表示基於特徵對例項進行分類的過程。
分類決策樹模型是一種描述對例項進行分類的樹形結構。決策樹由結點(node)和有向邊(directed edge)組成。結點有兩種型別:內部結點(internal node)和葉結點(leaf node)。內部結點表示一個特徵或屬性,葉結點表示一個類。一般的,一棵決策樹包含一個根節點,若干個內部節點和若干個葉節點;葉節點對應於決策的結果,其他每個節點對應於一個屬性測試。決策樹學習的目的是生成一顆泛化能力強,即可以處理未見過的資料的決策樹。左圖為一個一般的決策樹模型。右圖為一個判斷生物是否為魚類的決策樹例項。


決策樹學習本質上是從訓練資料集中歸納出一組分類規則,與訓練資料集不相矛盾的決策樹,即能對訓練資料集進行正確分類的決策樹。這規則可能有多個,也可能一個也沒有。上圖右有兩個規則,分別是:1、不浮出水面是否能生存 ;2、是否有腳蹼。決策樹學習是由訓練資料集估計條件概率模型。我們選擇的條件概率模型不僅應該對訓練資料有很好的擬合、對未知資料也應該有很好的預測能力。
決策樹學習用損失函式實現這一目標。決策樹學習的損失函式通常是正則化的極大似然函式。決策樹學習的策略是以損失函式為目標函式的最小化。
決策樹學習的演算法通常是一個遞迴的選擇最優特徵,並根據該特徵對訓練資料進行分割,使得對各個子資料集有一個最好的分類的過程。1、首先構建根節點,將所有資料都放置到根節點內;2、選擇一個最優特徵,按照這個最優特徵將資料集分割成若干個子資料集使得子資料集有一個在當前條件下最好的分類;3、如果這些子資料集已經能夠基本被正確的分類,那麼就構建葉節點,並將這些子資料集分到對應的葉節點中去;4、如果這些子資料集還不能被基本正確的分類那麼就分別對這些子資料集選擇最優特徵,繼續構建新的節點;5、遞迴迴圈以上步驟,直到將所有資料進行了正確的劃分。最後每個例項都會被劃分到對應的葉節點上,即都有了分類,這就生成了一棵決策樹。
以上生成的決策樹可能對訓練資料有很好的分類能力,但是對陌生資料卻未必有很好的分類能力,即過擬合現象。所以我們需要採取措施使得決策樹有很好的泛化能力。一般會採用剪枝操作來使得我們的決策樹變得更簡單,從而獲得更好的泛化能力。具體操作就是剪去過於細分的葉節點,使其退回到父節點,甚至更高的節點,然後將父節點或者更高的節點作為新的葉節點。
從中我們可以看出,決策樹學習演算法包含特徵選擇、決策樹的生成、以及決策樹的剪枝。
二 特徵選擇
特徵選擇在於選取對訓練資料具有分類能力的特徵。這樣可以提高決策樹學習的效率,如果利用一個特徵進行分類的結果與隨機分類的結果沒有很大差別,則稱這個特徵是沒有分類能力的。經驗上扔掉這樣的特徵對決策樹學習的精度影響不大。通常特徵選擇的標準是資訊增益(information gain)或資訊增益比。
2.1特徵選擇的標準
特徵選擇是決定用哪個特徵來劃分特徵空間。假如有一堆豆子,由黃豆跟綠豆組成,那麼如何來劃分這堆豆子呢?很明顯,你會選擇用顏色來區分。當然你也可以選擇重量特徵來劃分,但是重量特徵劃分的而效果遠遠比不上顏色特徵的劃分效果。所以顏色特徵就是我們選擇的劃標準。但實際問題通常比這複雜得多,我們往往不能直接通過觀察得出首先使用哪一種特徵來劃分資料集。因此我們採用資訊增益作為標準來選擇特徵。資訊增益越大的特徵,越能幫助我們來有效的劃分資料集。
2.2資訊增益
2.2.1 熵
介紹資訊增益之前我們必須先介紹一下 熵 。在資訊理論與概率統計中,熵是表示隨機變數不確定性的度量。設 X 是一個取有限個值的離散隨機變數,那麼其概率分佈為:
則隨機變數 X 的熵定義為:
在式中,對數以2為底。有定義知,熵只依賴於X 的分佈,而與X 的值無關,所以也可以將X 的熵記作 H(p),即
熵的全稱為夏農熵或經驗熵,這個名字來源於資訊理論之父 克勞德·夏農。熵自誕生的那一天起,就註定會令世人十分費解。克勞德·夏農寫完資訊理論之後,約翰·馮·諾依曼建議使用"熵"這個術語,因為大家都不知道它是什麼意思。
2.2.2 條件熵
條件熵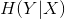
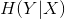
這裡,
2.2.3 資訊增益
資訊增益表示得知特徵 X 的資訊而使得類 Y 的資訊的不確定性減小的程度。特徵 A 對訓練資料集 D 的資訊增益 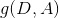
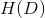
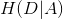
決策樹學習應該用資訊增益準則來選取特徵。給定訓練資料集 D 和特徵 A ,經驗熵 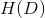
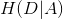
上面這一大段話讀起來晦澀難懂,但卻是對資訊增益一個非常特切的描述。那麼就讓我們用白話文再來翻譯一遍。現在有一窩貓 D 需要你將他們劃分為幾個類別。剛開始你無從先手,但是這堆東西都有幾個共同的特點(比如,特點A:長有黃色的毛,紅色的毛,綠色的毛;特點B:長毛,短毛,捲毛;特點C:會掉毛,不會掉毛)。如果你選擇按照特徵 A (毛的顏色)來劃分,你就會發現容易了很多。那麼如何界定這個容易呢?因為我現在能夠獲取更多的資訊了,而不是剛開始一籌莫展的樣子了。我從剛開始只有一點點資訊,通過找到特徵 A 我現在能夠獲得更多的資訊來劃分這一窩貓。這個過程我們使用數學來表示,就是資訊增益。但是你發現使用特徵 B(毛長)來劃分,會更容易。那麼這個特徵 B 就是我們目前需要的最佳特徵。
根據資訊增益準則的特徵選擇方法是:對訓練資料集 D ,計算其每個特徵的資訊增益,並比較他們的大小,選擇資訊增益最大的特徵。
設訓練資料集 D,|D| 表示其樣本容量,即樣本個數。設有 K 個類 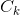
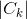
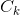
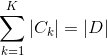
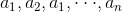
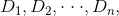
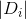
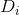
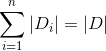
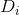
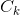
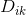
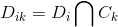
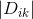
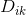
輸入:訓練資料集 D 的特徵 A :
輸出:特徵 A 對訓練資料集 D 的資訊增益 個 g(D,A)。
(1)計算資料集 D 的經驗熵 H(D)
(2)計算特徵 A 對資料集 D 的經驗條件熵H(D|A)
(3)計算資訊增益
2.2.4 練習題
現在來做一下習題,加深對資訊增益的認識:貸款申請樣本資料表
| ID | 年齡 | 有工作 | 有自己的房子 | 信貸情況 | 類別 |
| 1 | 青年 | 否 | 否 | 一般 | 否 |
| 2 | 青年 | 否 | 否 | 好 | 否 |
| 3 | 青年 | 是 | 否 | 好 | 是 |
| 4 | 青年 | 是 | 是 | 一般 | 是 |
| 5 | 青年 | 否 | 否 | 一般 | 否 |
| 6 | 中年 | 否 | 否 | 一般 | 否 |
| 7 | 中年 | 否 | 否 | 好 | 否 |
| 8 | 中年 | 是 | 是 | 好 | 是 |
| 9 | 中年 | 否 | 是 | 非常好 | 是 |
| 10 | 中年 | 否 | 是 | 非常好 | 是 |
| 11 | 老年 | 否 | 是 | 非常好 | 是 |
| 12 | 老年 | 否 | 是 | 好 | 是 |
| 13 | 老年 | 是 | 否 | 好 | 是 |
| 14 | 老年 | 是 | 否 | 非常好 | 是 |
| 15 | 老年 | 否 | 否 | 一般 | 否 |
解:
首先計算經驗熵H(D)即夏農熵:
然後計算各特徵對資料集D 的資訊增益。分別以 A1,A2,A3,A4 表示年齡、有工作、有自己的房子和信貸4個特徵
(1)
(2)
(3)
(4)
最後發現A3的資訊增益最大,所以將A3作為最優特徵
3程式碼實現
3.1計算給定資料集 D 的經驗熵H(D)即夏農熵:
- 我們首先需要將資料集轉化為我們需要的格式,即矩陣。統計所有類別的總數,這裡是15
- 然後再利用字典記錄每一個類別的個數:“no”是6,“yes“是9,之後計算每個類別的概率:“no”是6/15,“yes“是9/15
- 根據夏農熵公式計算資料集 D 的夏農熵:0.97095
from math import log
def createDataSet():
dataSet = [['青年', '否', '否', '一般', 'no'],
[ '青年', '否', '否', '好', 'no'],
[ '青年', '是', '否', '好', 'yes'],
[ '青年', '是', '是', '一般', 'yes'],
[ '青年', '否', '否', '一般', 'no'],
[ '中年', '否', '否', '一般', 'no'],
[ '中年', '否', '否', '好', 'no'],
[ '中年', '是', '是', '好', 'yes'],
[ '中年', '否', '是', '非常好', 'yes'],
[ '中年', '否', '是', '非常好', 'yes'],
[ '老年', '否', '是', '非常好', 'yes'],
[ '老年', '否', '是', '好', 'yes'],
[ '老年', '是', '否', '好', 'yes'],
[ '老年', '是', '否', '非常好', 'yes'],
[ '老年', '否', '否', '一般', 'no']]
labels = ['年齡', '有工作', '有自己的房子', '信貸情況']
return dataSet
"""
DataSet:給定的資料集
Function:計算給定資料集的香濃熵
return:返回的是計算好的香濃熵
"""
def ShannonEnt(dataSet):
len_dataSet = len(dataSet) #樣本資料的個數
label_class = {} #用來記錄每個樣本類別的個數
Ent = 0.0 #用來儲存經驗熵
for item in dataSet: #迴圈讀入例項
if item[-1] not in label_class.keys(): #如果儲存類別的的字典內沒有現在的類別,那麼就建立一個以當前類別為key值的元素
label_class[item[-1]] = 0 #並將其value值賦值為0
label_class[item[-1]] += 1 #如果字典內已經存在此類別,那麼將其value加 1,即當前類別的個數加一
for lable in label_class: #從字典內迴圈獲取所有的類別
P = float(label_class[lable]) / len_dataSet #計算當前類別佔總樣本資料的比例,即當前類別出現的概率
Ent -= P * log(P, 2) #計算所有類別的香濃熵
return Ent
if __name__ == "__main__":
dataSet=createDataSet()
Ent=ShannonEnt(dataSet)
print(dataSet)
print(Ent)
輸出結果如下,首先列印原始的輸入資料集,然後列印計算出來的經驗熵 0.97095
[['青年', '否', '否', '一般', 'no'], ['青年', '否', '否', '好', 'no'], ['青年', '是', '否', '好', 'yes'], ['青年', '是', '是', '一般', 'yes'], ['青年', '否', '否', '一般', 'no'], ['中年', '否', '否', '一般', 'no'], ['中年', '否', '否', '好', 'no'], ['中年', '是', '是', '好', 'yes'], ['中年', '否', '是', '非常好', 'yes'], ['中年', '否', '是', '非常好', 'yes'], ['老年', '否', '是', '非常好', 'yes'], ['老年', '否', '是', '好', 'yes'], ['老年', '是', '否', '好', 'yes'], ['老年', '是', '否', '非常好', 'yes'], ['老年', '否', '否', '一般', 'no']]
0.9709505944546686
Process finished with exit code 03.2將資料集按照給定的特徵進行分類
我們為什麼要根據特徵來將資料集進行劃分呢?或者說,我們要對資料集劃分的目的是什麼?這其實是為了方便計算每個特徵下的經驗條件熵。那麼為什麼要計算經驗條件熵呢?是為了計算基於特徵 A 的資訊增益。
我們將資料集按照我們給定的 特徵 的 值 (比如,特徵是毛的顏色,特徵的值是黃毛)進行劃分,這樣我們就可以計算出在黃毛的特徵值的情況下夏農熵。然後可以計算紅毛,綠毛的夏農熵。全部計算完之後就可以計算特徵 A 的經驗條件熵了。計算出經驗條件熵之後就可以計算資訊增益了。所以這是一個環環相扣的環節。所以計算資訊增益可以細分為以下步驟:
- 首先計算整個資料集 D 的經驗熵,即夏農熵 H(D)
- 計算基於特徵 A 的條件經驗熵
- 首先將資料集基於特徵 A(毛的顏色) 的 值(黃毛) 進行劃分,即新的資料集只留下特徵 A 的值(毛的顏色為黃毛)的資料
- 計算新的資料集,即毛的顏色為黃毛的資料集的經驗熵。並將經驗熵乘以黃毛佔整個毛的顏色的概率。
- 重複上述步驟,計算特徵 A 剩下的值(紅毛、綠毛)的經驗熵,並將所有值的經驗熵加起來,得到 H(D|A)
3. 計算資訊增益 即: H(D) - H(D|A)
from math import log
def createDataSet():
dataSet = [['青年', '否', '否', '一般', 'no'],
[ '青年', '否', '否', '好', 'no'],
[ '青年', '是', '否', '好', 'yes'],
[ '青年', '是', '是', '一般', 'yes'],
[ '青年', '否', '否', '一般', 'no'],
[ '中年', '否', '否', '一般', 'no'],
[ '中年', '否', '否', '好', 'no'],
[ '中年', '是', '是', '好', 'yes'],
[ '中年', '否', '是', '非常好', 'yes'],
[ '中年', '否', '是', '非常好', 'yes'],
[ '老年', '否', '是', '非常好', 'yes'],
[ '老年', '否', '是', '好', 'yes'],
[ '老年', '是', '否', '好', 'yes'],
[ '老年', '是', '否', '非常好', 'yes'],
[ '老年', '否', '否', '一般', 'no']]
labels = ['年齡', '有工作', '有自己的房子', '信貸情況']
return dataSet
"""
dataSet: 給定的資料集
axis: 給定的特徵的索引值
value: 對應索引的值
new_dataset: 根據給定的特徵劃分的新資料
Function:按照給定的特徵將資料集分類成新的資料集
"""
def splitDataSet(dataSet, axis, value):
new_dataset = []
for item in dataSet: #迴圈讀入資料集的每一行資料
if item[axis] == value: #如果是我們需要的特徵的資料就將其存放到新的陣列中
templet_set = item[:axis] #中間變數,用於存放獲取的特徵變數所在行的其他資料
templet_set.extend(item[axis+1:]) #a=[1,2,3], b=[4,5,6] a.extend(b)=[1, 2, 3, 4, 5, 6]
new_dataset.append(templet_set) #a=[1,2,3], b=[4,5,6] a.append(b)=[1, 2, 3, [4,5,6] ]
return new_dataset
if __name__ == "__main__":
dataSet=createDataSet()
new_dataSet=splitDataSet(dataSet,0,'青年')
print("這是原始資料集:")
print(dataSet)
print("這是新資料集:")
for item in new_dataSet:
print(item)
然後我們獲得的結果如下:
這是原始資料集:
[['青年', '否', '否', '一般', 'no'], ['青年', '否', '否', '好', 'no'], ['青年', '是', '否', '好', 'yes'], ['青年', '是', '是', '一般', 'yes'], ['青年', '否', '否', '一般', 'no'], ['中年', '否', '否', '一般', 'no'], ['中年', '否', '否', '好', 'no'], ['中年', '是', '是', '好', 'yes'], ['中年', '否', '是', '非常好', 'yes'], ['中年', '否', '是', '非常好', 'yes'], ['老年', '否', '是', '非常好', 'yes'], ['老年', '否', '是', '好', 'yes'], ['老年', '是', '否', '好', 'yes'], ['老年', '是', '否', '非常好', 'yes'], ['老年', '否', '否', '一般', 'no']]
這是新資料集:
['否', '否', '一般', 'no']
['否', '否', '好', 'no']
['是', '否', '好', 'yes']
['是', '是', '一般', 'yes']
['否', '否', '一般', 'no']
Process finished with exit code 0
3.3根據資訊增益選擇最佳特徵
既然我們做好了前面的準備工作那麼我們現在就可以計算出每個特徵的資訊增益了,步驟如下:
- 計算總共有多少個特徵
- 獲得特徵 A 的所有的值,計算第一個值的經驗熵,迴圈遍歷所有值的經驗熵,從而計算特徵 A 的條件經驗熵,進而獲得資訊增益
- 迴圈所有特徵,計算所有特徵的資訊增益。
- 比較所有的資訊增益,獲得最大的資訊增益,方法是採用氣泡排序的思路
from math import log
def createDataSet():
dataSet = [['青年', '否', '否', '一般', 'no'],
[ '青年', '否', '否', '好', 'no'],
[ '青年', '是', '否', '好', 'yes'],
[ '青年', '是', '是', '一般', 'yes'],
[ '青年', '否', '否', '一般', 'no'],
[ '中年', '否', '否', '一般', 'no'],
[ '中年', '否', '否', '好', 'no'],
[ '中年', '是', '是', '好', 'yes'],
[ '中年', '否', '是', '非常好', 'yes'],
[ '中年', '否', '是', '非常好', 'yes'],
[ '老年', '否', '是', '非常好', 'yes'],
[ '老年', '否', '是', '好', 'yes'],
[ '老年', '是', '否', '好', 'yes'],
[ '老年', '是', '否', '非常好', 'yes'],
[ '老年', '否', '否', '一般', 'no']]
labels = ['年齡', '有工作', '有自己的房子', '信貸情況']
return dataSet
"""
DataSet:給定的資料集
Function:計算給定資料集的香濃熵
return:返回的是計算好的香濃熵
"""
def ShannonEnt(dataSet):
len_dataSet = len(dataSet) #樣本資料的個數
label_class = {} #用來記錄每個樣本類別的個數
Ent = 0.0 #用來儲存經驗熵
for item in dataSet: #迴圈讀入例項
if item[-1] not in label_class.keys(): #如果儲存類別的的字典內沒有現在的類別,那麼就建立一個以當前類別為key值的元素
label_class[item[-1]] = 0 #並將其value值賦值為0
label_class[item[-1]] += 1 #如果字典內已經存在此類別,那麼將其value加 1,即當前類別的個數加一
for lable in label_class: #從字典內迴圈獲取所有的類別
P = float(label_class[lable]) / len_dataSet #計算當前類別佔總樣本資料的比例,即當前類別出現的概率
Ent -= P * log(P, 2) #計算所有類別的香濃熵
return Ent
"""
dataSet: 給定的資料集
axis: 給定的特徵的索引值
value: 對應索引的值
new_dataset: 根據給定的特徵劃分的新資料
Function:按照給定的特徵將資料集分類成新的資料集
"""
def splitDataSet(dataSet, axis, value):
new_dataset = []
for item in dataSet: #迴圈讀入資料集的每一行資料
if item[axis] == value: #如果是我們需要的特徵的資料就將其存放到新的陣列中
templet_set = item[:axis] #中間變數,用於存放獲取的特徵變數所在行的其他資料
templet_set.extend(item[axis+1:]) #a=[1,2,3], b=[4,5,6] a.extend(b)=[1, 2, 3, 4, 5, 6]
new_dataset.append(templet_set) #a=[1,2,3], b=[4,5,6] a.append(b)=[1, 2, 3, [4,5,6] ]
return new_dataset
"""
dataSet: 輸入的資料集
Function: 選擇資訊增益最大的特徵
return: 返回的是資訊增益最大的特徵在DataSet中的列索引值
"""
def chooseBestFeature(dataSet):
len_lables = len(dataSet[0]) - 1 #獲取資料集的特徵總數。減去的是資料集的類別
base_Ent = ShannonEnt(dataSet) #獲得總資料集的夏農熵
base_InfoGain = 0.0 #用於記錄當前最佳資訊增益
best_lables = -1 #用於記錄獲得最佳資訊增益的特徵的索引值
for i in range(len_lables): #獲取每個特徵相應的夏農熵
lable_list = [items[i] for items in dataSet] #利用列表生成式獲取相應特徵下的分類,item表示為dataSet的單行資料,item[i]表示對應資料的具體數值
unique_value = set(lable_list) #利用集合獲得唯一的資料特徵,set跟數學中的集合概念類似,裡面沒有重複的元素
new_Ent = 0.0 #用於存放當前子類資料集的經驗條件熵
for value in unique_value: #獲取單個特徵值下的對應值例如:青年,中年, 老年
sub_dataset = splitDataSet(dataSet, i, value) #按照當前的特徵值將資料集進行劃分
prob = len(sub_dataset) / float(len(dataSet)) #獲得當前特徵的資料佔總資料的比例,即概率
new_Ent += prob * ShannonEnt(sub_dataset) #獲得當前類別的經驗條件熵
info_Gain = base_Ent - new_Ent #獲得當前的資訊增益
print("第",i,"個特徵的資訊增益為 ",info_Gain)
if(info_Gain > base_InfoGain):
base_InfoGain = info_Gain #如果遇見更好的資訊增益,就將更好的資訊增益賦值給best_InfoGain,並且記錄下當前資訊增益的特徵值的索引值
best_lables = i
print("最好的特徵索引值為:",best_lables)
return best_lables
if __name__ == "__main__":
dataSet=createDataSet()
new_dataSet=splitDataSet(dataSet,0,'青年')
print("這是原始資料集:")
print(dataSet)
print("這是新資料集:")
for item in new_dataSet:
print(item)
print("現在是計算的最好的特徵的索引值:")
best_lable=chooseBestFeature(dataSet)
print(best_lable)我們獲得的結果如下:
這是原始資料集:
[['青年', '否', '否', '一般', 'no'], ['青年', '否', '否', '好', 'no'], ['青年', '是', '否', '好', 'yes'], ['青年', '是', '是', '一般', 'yes'], ['青年', '否', '否', '一般', 'no'], ['中年', '否', '否', '一般', 'no'], ['中年', '否', '否', '好', 'no'], ['中年', '是', '是', '好', 'yes'], ['中年', '否', '是', '非常好', 'yes'], ['中年', '否', '是', '非常好', 'yes'], ['老年', '否', '是', '非常好', 'yes'], ['老年', '否', '是', '好', 'yes'], ['老年', '是', '否', '好', 'yes'], ['老年', '是', '否', '非常好', 'yes'], ['老年', '否', '否', '一般', 'no']]
這是新資料集:
['否', '否', '一般', 'no']
['否', '否', '好', 'no']
['是', '否', '好', 'yes']
['是', '是', '一般', 'yes']
['否', '否', '一般', 'no']
現在是計算的最好的特徵的索引值:
第 0 個特徵的資訊增益為 0.08300749985576883
第 1 個特徵的資訊增益為 0.32365019815155627
第 2 個特徵的資訊增益為 0.4199730940219749
第 3 個特徵的資訊增益為 0.36298956253708536
最好的特徵索引值為: 2
2
Process finished with exit code 0


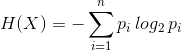
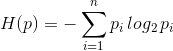
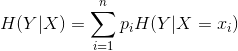
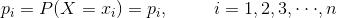
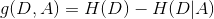
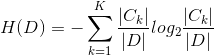
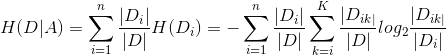
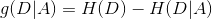
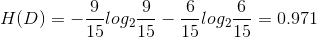
![g(D|A_{1})=H(D)-[\frac{5}{15}H(D_{1})+\frac{5}{15}H(D_{2})+\frac{5}{15}H(D_{3})]](https://img-blog.csdnimg.cn/20181224221248457)
![=0.971-\left [ \frac{5}{15}\left ( - \frac{2}{5}log_{2}\frac{2}{5}- \frac{3}{5}log_{2}\frac{3}{5}\right )+ \frac{5}{15}\left ( - \frac{3}{5}log_{2}\frac{3}{5}- \frac{2}{5}log_{2}\frac{2}{5}\right )+ \frac{5}{15}\left ( - \frac{4}{5}log_{2}\frac{4}{5}- \frac{1}{5}log_{2}\frac{1}{5}\right ) \right ]](https://img-blog.csdnimg.cn/20181224221248472)
![=0.971-\left [ \frac{5}{15} \times 0+ \frac{10}{15}\left ( - \frac{4}{10} log_{2} \frac{4}{10}- \frac{6}{10} log_{2} \frac{6}{10} \right ) \right ]=0.324](https://img-blog.csdnimg.cn/20181225135749129)
![g(D,A_{3})=0.971-\left [\frac{6}{15} \times 0+\frac{9}{15} \left ( -\frac{3}{9} log_{2}\frac{3}{9} -\frac{6}{9} log_{2}\frac{6}{9} \right ) \right ]=0.971-0.551=0.420](https://img-blog.csdnimg.cn/20181225135749151)