閱讀目錄

• 知識點
• 感知機
• k近鄰法
• 樸素貝葉斯
• 決策樹
• logistic迴歸和最大熵模型
• 支援向量機
• 提升方法
• EM演算法
• 隱馬爾可夫模型(HMM)
• 統計學習方法總結
• 神經網路
• K-Means
• Bagging
• Apriori
• 降維方法
• 引用

因為要準備面試,本文以李航的《統計學習方法》為主,結合西瓜書等其他資料對機器學習知識做一個整理.

回到頂部

知識點

• 程序和執行緒:程序和執行緒都是一個時間段的描述，是CPU工作時間段的描述，不過是顆粒大小不同.程序就是包換上下文切換的程式執行時間總和 = CPU載入上下文+CPU執行+CPU儲存上下文.執行緒是共享了程序的上下文環境的更為細小的CPU時間段。
• 判別式模型和生成式模型:

1. 判別式模型直接學習決策函式f(X)或條件概率分佈P(Y|X)作為預測的模型.往往準確率更高,並且可以簡化學習問題.如k近鄰法/感知機/決策樹/最大熵模型/Logistic迴歸/線性判別分析(LDA)/支援向量機(SVM)/Boosting/條件隨機場演算法(CRF)/線性迴歸/神經網路
2. 生成式模型由資料學習聯合概率分佈P(X,Y),然後由P(Y|X)=P(X,Y)/P(X)求出條件概率分佈作為預測的模型,即生成模型.當存在隱變數時只能用生成方法學習.如混合高斯模型和其他混合模型/隱馬爾可夫模型(HMM)/樸素貝葉斯/依賴貝葉斯(AODE)/LDA文件主題生成模型

• 概率質量函式,概率密度函式,累積分佈函式
  :

1. 概率質量函式 (probability mass function，PMF)是離散隨機變數在各特定取值上的概率。
2. 概率密度函式（p robability density function，PDF ）是對 連續隨機變數 定義的，本身不是概率，只有對連續隨機變數的取值進行積分後才是概率。
3. 累積分佈函式（cumulative distribution function，CDF） 能完整描述一個實數隨機變數X的概率分佈，是概率密度函式的積分。對於所有實數x ，與pdf相對。

• 極大似然估計:已知某個引數能使這個樣本出現的概率最大，我們當然不會再去選擇其他小概率的樣本，所以乾脆就把這個引數作為估計的真實值
• 最小二乘法:二乘的英文是least square,找一個（組）估計值,使得實際值與估計值之差的平方加總之後的值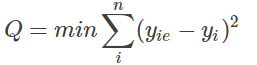最小.求解方式是對引數求偏導,令偏導為0即可.樣本量小時速度快.
• 梯度下降法:負梯度方向是函式值下降最快的方向,每次更新值都等於原值加學習率(步長)乘損失函式的梯度.每次都試一個步長看會不會下降一定的程度,如果沒有的話就按比例減小步長.不斷應用該公式直到收斂,可以得到區域性最小值.初始值的不同組合可以得到不同區域性最小值.在最優點時會有震盪.

1. 批量梯度下降(BGD):每次都使用所有的m個樣本來更新,容易找到全域性最優解,但是m較大時速度較慢
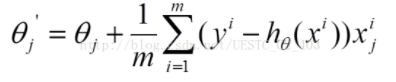
2. 隨機梯度下降(SGD):每次只使用一個樣本來更新,訓練速度快,但是噪音較多,不容易找到全域性最優解,以損失很小的一部分精確度和增加一定數量的迭代次數為代價,換取了總體的優化效率的提升.注意控制步長縮小,減少震盪.
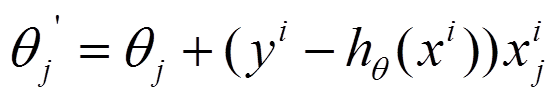
3. 小批量梯度下降(MBGD):每次使用一部分樣本來更新.

• 牛頓法:牛頓法是二次收斂,因此收斂速度快.從幾何上看是每次用一個二次曲面來擬合當前所處位置的局部曲面,而梯度下降法是用一個平面來擬合.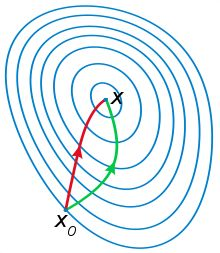紅色的是牛頓法的迭代路徑,綠色的是梯度下降法的迭代路徑.牛頓法起始點不能離極小點太遠,否則很可能不會擬合.

1. 黑塞矩陣是由目標函式f(x)在點X處的二階偏導陣列成的n*n階對稱矩陣。
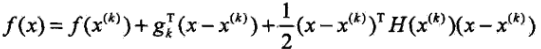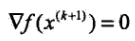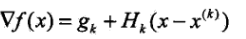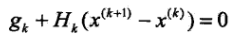2. 牛頓法:將f(x)在x(k)附近進行二階泰勒展開:,其中gk是f(x)的梯度向量在x(k)的值,H(x(k))是f(x)的黑塞矩陣在點x(k)的值.牛頓法利用極小點的必要條件f(x)處的梯度為0,每次迭代中從點x(k)開始,假設,對二階泰勒展開求偏導有,代入得到,即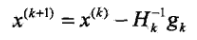,以此為迭代公式就是牛頓法.

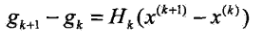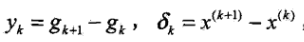• 擬牛頓法:用一個n階正定矩陣Gk=G(x(k))來近似代替黑塞矩陣的逆矩陣就是擬牛頓法的基本思想.在牛頓法中黑塞矩陣滿足的條件如下:,令,則有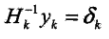,稱為擬牛頓條件.根據選擇Gk方法的不同有多種具體實現方法.

1. DFP演算法:假設每一步,為使Gk+1滿足擬牛頓條件,可使Pk和Qk滿足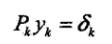,,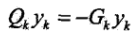例如取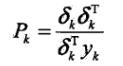,,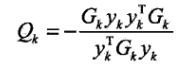就得到迭代公式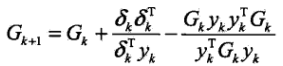

2.  BFGS演算法: 最流行的擬牛頓演算法.考慮用Bk逼近黑塞矩陣,此時相應的擬牛頓條件是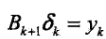,假設每一步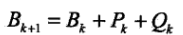,則Pk和Qk滿足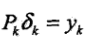,,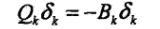類似得到迭代公式.

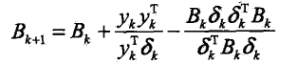• 先驗概率和後驗概率:

1. 先驗概率就是事情發生前的預測概率.
2. 後驗概率是一種條件概率，它限定了事件為隱變數取值，而條件為觀測結果。一般的條件概率，條件和事件可以是任意的.
3. 貝葉斯公式P(y|x) = ( P(x|y) * P(y) ) / P(x)中,P(y|x)是後驗概率,P(x|y)是條件概率,P(y)是先驗概率.

• 偏差,方差,噪聲:

1. 偏差:度量了學習演算法的期望預測和真實結果偏離程度
2. 方差:度量了同樣大小的訓練集的變動所導致的學習效能的變化，即刻畫了資料擾動所造成的影響
3. 噪聲:可以認為是資料自身的波動性，表達了目前任何學習演算法所能達到泛化誤差的下限
4. 泛化誤差可以分解為偏差、方差與噪聲之和

• 對偶原理:一個優化問題可以從主問題和對偶問題兩個方面考慮.在推導對偶問題時,通過將拉格朗日函式對x求導並使導數為0來獲得對偶函式.對偶函式給出了主問題最優解的下界,因此對偶問題一般是凸問題,那麼只需求解對偶函式的最優解就可以了.
• KKT條件:通常我們要求解的最優化條件有如下三種:

1. 無約束優化問題:通常使用求導,使導數為零,求解候選最優值
2. 有等式約束的優化問題:通常使用拉格朗日乘子法,即把等式約束用拉格朗日乘子和優化問題合併為一個式子,通過對各個變數求導使其為零,求解候選最優值.拉格朗日乘數法其實是KKT條件在等式約束優化問題的簡化版.
3. 有不等式約束的優化問題:通常使用KKT條件.即把不等式約束,等式約束和優化問題合併為一個式子.假設有多個等式約束h(x)和不等式約束g(x),則不等式約束引入的KKT條件如下:,實質是最優解在g(x)<0區域內時,約束條件不起作用,等價於對μ置零然後對原函式的偏導數置零;當g(x)=0時與情況2相近.結合兩種情況,那麼只需要使L對x求導為零,使h(x)為零,使μg(x)為零三式即可求解候選最優值.

• 效能度量:

1. 準確度,最常用,但在資料集不平衡的情況下不好
2. Precision(精確度/查準率):P=TP/(TP+FP)
3. Recall(召回率/查全率):R=TP/(TP+FN)
4. Fβ度量: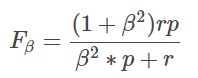,當β=1時退化為F1度量,是精確率和召回率的調和均值.
5. TPR(真正例率):TPR=TP/(TP+FN)
6. FPR(假正例率):FPR=FP/(TN+FP)
7. PR曲線:縱軸為Precision,橫軸為Recall,一般使用平衡點(BEP,即Precsion=Recall的點)作為衡量標準.
8. ROC(接受者操作特徵)曲線:縱軸為TRP,橫軸為FPR,在繪圖時將分類閾值依次設為每個樣例的預測值,再連線各點.ROC曲線圍住的面積稱為AOC,AOC越大則學習器效能越好.

• 損失函式和風險函式:

1. 損失函式度量模型一次預測的好壞.常用的損失函式有:0-1損失函式,平方損失函式,絕對損失函式,對數似然損失函式.
2. 損失函式的期望是理論上模型關於聯合分佈P(X,Y)的平均意義下的損失,稱為風險函式,也叫期望風險.但是聯合分佈是未知的,期望風險不能直接計算.
3. 當樣本容量N趨於無窮時經驗風險趨於期望風險,但現實中訓練樣本數目有限.

• 經驗風險最小化和結構風險最小化:

1. 模型關於訓練資料集的平均損失稱為經驗風險.經驗風險最小化的策略就是最小化經驗風險.當樣本數量足夠大時學習效果較好.比如當模型是條件概率分佈,損失函式是對數損失函式時,經驗風險最小化就等價於極大似然估計.但是當樣本容量很小時會出現過擬合.
2. 結構風險最小化等於正則化.結構風險在經驗風險上加上表示模型複雜度的正則化項.比如當模型是條件概率分佈,損失函式是對數損失函式,模型複雜度由模型的先驗概率表示時,結構風險最小化就等價於最大後驗概率估計.

• 過擬合是指學習時選擇的模型所包含的引數過多,以致於對已知資料預測得很好,但對未知資料預測很差的現象.模型選擇旨在避免過擬合併提高模型的預測能力.
• 正則化是模型選擇的典型方法.正則化項一般是模型複雜度的單調遞增函式,比如模型引數向量的範數.
• 交叉驗證是另一常用的模型選擇方法,可分為簡單交叉驗證,K折交叉驗證,留一交叉驗證等.

回到頂部

感知機

• 感知機是二類分類的線性模型,屬於判別模型.感知機學習旨在求出將訓練資料進行線性劃分的分離超平面.是神經網路和支援向量機的基礎.
• 模型: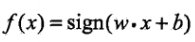,w叫作權值向量,b叫做偏置,sign是符號函式.

   

• 感知機的幾何解釋:wx+b對應於特徵空間中的一個分離超平面S,其中w是S的法向量,b是S的截距.S將特徵空間劃分為兩個部分,位於兩個部分的點分別被分為正負兩類.
• 策略:假設訓練資料集是線性可分的,感知機的損失函式是誤分類點到超平面S的總距離.因為誤分類點到超平面S的距離是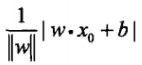,且對於誤分類的資料來說,總有成立,因此不考慮1/||w||,就得到感知機的損失函式: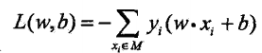,其中M是誤分類點的集合.感知機學習的策略就是選取使損失函式最小的模型引數.

• 演算法:感知機的最優化方法採用隨機梯度下降法.首先任意選取一個超平面w0,b0,然後不斷地極小化目標函式.在極小化過程中一次隨機選取一個誤分類點更新w,b,直到損失函式為0.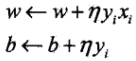,其中η表示步長.該演算法的直觀解釋是:當一個點被誤分類,就調整w,b使分離超平面向該誤分類點接近.感知機的解可以不同.

• 對偶形式:假設原始形式中的w0和b0均為0,設逐步修改w和b共n次,令a=nη,最後學習到的w,b可以表示為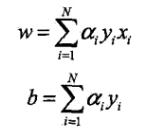.那麼對偶演算法就變為設初始a和b均為0,每次選取資料更新a和b直至沒有誤分類點為止.對偶形式的意義在於可以將訓練集中例項間的內積計算出來,存在Gram矩陣中,可以大大加快訓練速度.

回到頂部

k近鄰法

• k近鄰法根據其k個最近鄰的訓練例項的類別,通過多數表決等方式進行預測.k值的選擇,距離度量及分類決策規則是k近鄰法的三個基本要素.當k=1時稱為最近鄰演算法.
• 模型:當訓練集,距離度量,k值以及分類決策規則確定後,特徵空間已經根據這些要素被劃分為一些子空間,且子空間裡每個點所屬的類也已被確定.
• 策略:

1. 距離:特徵空間中兩個例項點的距離是相似程度的反映,k近鄰演算法一般使用歐氏距離,也可以使用更一般的Lp距離或Minkowski距離.
2. k值:k值較小時,整體模型變得複雜,容易發生過擬合.k值較大時,整體模型變得簡單.在應用中k一般取較小的值,通過交叉驗證法選取最優的k.
3. 分類決策規則:k近鄰中的分類決策規則往往是多數表決,多數表決規則等價於經驗風險最小化.

• 演算法:根據給定的距離度量,在訓練集中找出與x最鄰近的k個點,根據分類規則決定x的類別y.
• kd樹:

1. kd樹就是一種對k維空間中的例項點進行儲存以便對其進行快速檢索的樹形資料結構.kd樹更適用於訓練例項數遠大於空間維數時的k近鄰搜尋.
2. 構造:可以通過如下遞迴實現:在超矩形區域上選擇一個座標軸和此座標軸上的一個切分點,確定一個超平面,該超平面將當前超矩形區域切分為兩個子區域.在子區域上重複切分直到子區域內沒有例項時終止.通常依次選擇座標軸和選定座標軸上的中位數點為切分點,這樣可以得到平衡kd樹.
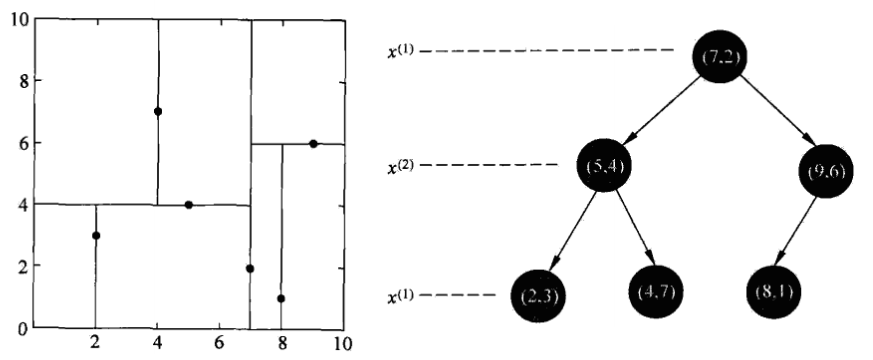
3. 搜尋:從根節點出發,若目標點x當前維的座標小於切分點的座標則移動到左子結點,否則移動到右子結點,直到子結點為葉結點為止.以此葉結點為"當前最近點",遞迴地向上回退,在每個結點:(a)如果該結點比當前最近點距離目標點更近,則以該結點為"當前最近點"(b)"當前最近點"一定存在於該結點一個子結點對應的區域,檢查該結點的另一子結點對應的區域是否與以目標點為球心,以目標點與"當前最近點"間的距離為半徑的超球體相交.如果相交,移動到另一個子結點,如果不相交,向上回退.持續這個過程直到回退到根結點,最後的"當前最近點"即為最近鄰點.

回到頂部

樸素貝葉斯

• 樸素貝葉斯是基於貝葉斯定理和特徵條件獨立假設的分類方法.首先學習輸入/輸出的聯合概率分佈,然後基於此模型,對給定的輸入x,利用貝葉斯定理求出後驗概率最大的輸出y.屬於生成模型.
• 模型:首先學習先驗概率分佈,然後學習條件概率分佈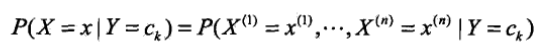.如果估計實際,需要指數級的計算,所以樸素貝葉斯法對條件概率分佈作了條件獨立性的假設,上式變成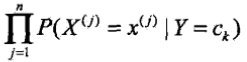.在分類時,通過學習到的模型計算後驗概率分佈,由貝葉斯定理得到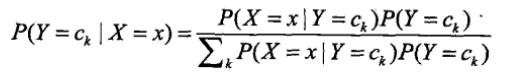,將條件獨立性假設得到的等式代入,並且注意到分母都是相同的,所以得到樸素貝葉斯分類器: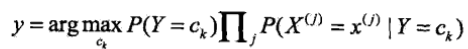
• 樸素貝葉斯將例項分到後驗概率最大的類中,這等價於期望風險最小化.
• 演算法:使用極大似然估計法估計相應的先驗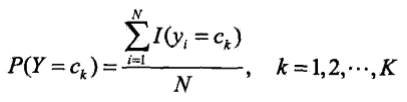概率和條件概率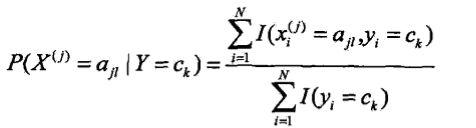,計算條件獨立性假設下的例項各個取值的可能性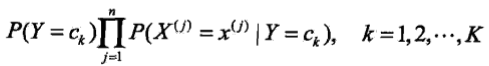,選取其中的最大值作為輸出.
• 用極大似然估計可能會出現所要估計的概率值為0的情況,在累乘後會影響後驗概率的計算結果,使分類產生偏差.可以採用貝葉斯估計,在隨機變數各個取值的頻數上賦予一個正數.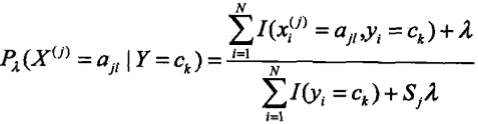.Sj為j屬性可能取值數量,當λ=0時就是極大似然估計.常取λ=1,稱為拉普拉斯平滑.
• 如果是連續值的情況,可以假設連續變數服從高斯分佈,然後用訓練資料估計引數.

   

回到頂部

決策樹

• 決策樹是一種基本的分類與迴歸方法.它可以認為是if-then規則的集合,也可以認為是定義在特徵空間與類空間上的條件概率分佈.主要優點是模型具有可讀性,分類速度快.
• 模型:分類決策樹由結點和有向邊組成.結點分為內部結點(表示一個特徵或屬性)和葉結點(表示一個類).決策樹的路徑具有互斥且完備的性質.
• 策略:決策樹學習本質上是從訓練資料集中歸納出一組分類規則.我們需要的是一個與訓練資料矛盾較小,同時具有很好的泛化能力的決策樹.從所有可能的決策樹中選取最優決策樹是NP完全問題,所以現實中常採用啟發式方法近似求解.
• 演算法:決策樹學習演算法包含特徵選擇,決策樹的生成與決策樹的剪枝過程.生成只考慮區域性最優,剪枝則考慮全域性最優.
• 特徵選擇:如果利用一個特徵進行分類的結果與隨機分類的結果沒有很大差別,則稱這個特徵是沒有分類能力的.扔掉這樣的特徵對決策樹學習的精度影響不大.

1. 資訊熵:熵是衡量隨機變數不確定性的度量.熵越大,隨機變數的不確定性就越大.資訊熵是資訊量的期望.條件熵表示在已知隨機變數X的條件下隨機變數Y的不確定性.
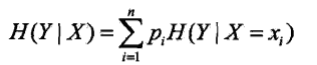
2. 資訊增益:表示得知特徵X的資訊而使得類Y的資訊的不確定性減少的程度.定義為集合D的經驗熵與特徵A在給定條件下D的經驗條件熵之差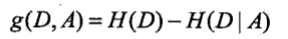,也就是訓練資料集中類與特徵的互資訊.
3. 資訊增益演算法:計算資料集D的經驗熵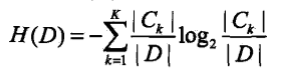,計算特徵A對資料集D的經驗條件熵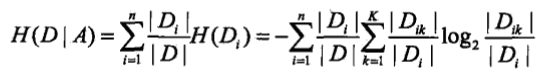,計算資訊增益,選取資訊增益最大的特徵.
4. 資訊增益比:資訊增益值的大小是相對於訓練資料集而言的,並無絕對意義.使用資訊增益比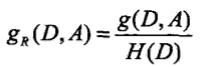可以對這一問題進行校正.

    

• 決策樹的生成:

1. ID3演算法:核心是在決策樹各個結點上應用資訊增益準則選擇資訊增益最大且大於閾值的特徵,遞迴地構建決策樹.ID3相當於用極大似然法進行概率模型的選擇.由於演算法只有樹的生成,所以容易產生過擬合.
2. C4.5演算法:C4.5演算法與ID3演算法相似,改用資訊增益比來選擇特徵.

• 決策樹的剪枝:

1. 在學習時過多考慮如何提高對訓練資料的正確分類,從而構建出過於複雜的決策樹,產生過擬合現象.解決方法是對已生成的決策樹進行簡化,稱為剪枝.
2. 設樹的葉結點個數為|T|,每個葉結點有Nt個樣本點,其中k類樣本點有Ntk個,剪枝往往通過極小化決策樹整體的損失函式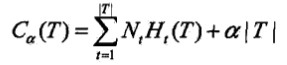來實現,其中經驗熵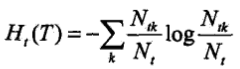.剪枝通過加入a|T|項來考慮模型複雜度,實際上就是用正則化的極大似然估計進行模型選擇.
3. 剪枝演算法:剪去某一子結點,如果生成的新的整體樹的損失函式值小於原樹,則進行剪枝,直到不能繼續為止.具體可以由動態規劃實現.

• CART演算法:

1. CART既可以用於分類也可以用於迴歸.它假設決策樹是二叉樹,內部結點特徵的取值為"是"和"否".遞迴地構建二叉樹,對迴歸樹用平方誤差最小化準則,對分類數用基尼指數最小化準則.
2. 迴歸樹的生成:在訓練資料集所在的輸入空間中,遞迴地將每個區域劃分為兩個子區域.選擇第j個變數和它取的值s作為切分變數和切分點,並定義兩個區域,遍歷變數j,對固定的j掃描切分點s,求解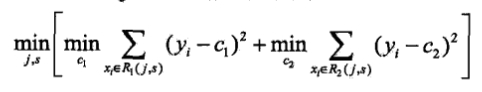.用選定的對(j,s)劃分區域並決定相應的輸出值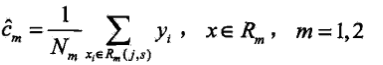,直到滿足停止條件.
3. 基尼指數:假設有K個類,樣本屬於第k類的概率為pk,則概率分佈的基尼指數為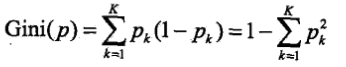,表示不確定性.在特徵A的條件下集合D的基尼指數定義為,表示分割後集合D的不確定性.基尼指數越大,樣本集合的不確定性也就越大.

4. 分類樹的生成:從根結點開始,遞迴進行以下操作:設結點的訓練資料集為D,對每個特徵A和其可能取的每個值a,計算A=a時的基尼指數,選擇基尼指數最小的特徵及其對應的切分點作為最優特徵與最優切分點,生成兩個子結點,直至滿足停止條件.停止條件一般是結點中的樣本個數小於閾值,或樣本集的基尼指數小於閾值,或沒有更多特徵.

5. CART剪枝:
   Tt表示以t為根結點的子樹,|Tt|是Tt的葉結點個數.可以證明當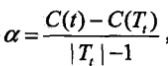時,Tt與t有相同的損失函式值,且t的結點少,因此t比Tt更可取,對Tt進行剪枝.自下而上地對各內部結點t計算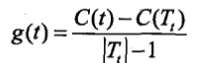,並令a=min(g(t)),自上而下地訪問內部節點t,如果有g(t)=a,進行剪枝,並對t以多數表決法決定其類,得到子樹T,如此迴圈地生成一串子樹序列,直到新生成的T是由根結點單獨構成的樹為止.利用交叉驗證法在子樹序列中選取最優子樹.

• 如果是連續值的情況,一般用二分法作為結點來劃分.

回到頂部

logistic迴歸和最大熵模型

• 邏輯斯諦分佈:分佈函式f(x)以點(μ,1/2)為中心對稱,γ的值越小,曲線在中心附近增長得越快.
• 邏輯斯諦迴歸模型:對於給定的輸入x,根據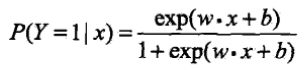和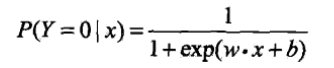計算出兩個條件概率值的大小,將x分到概率值較大的那一類.將偏置b加入到權值向量w中,並在x的最後新增常數項1,得到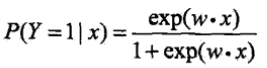和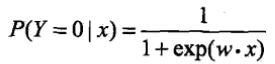.如果某事件發生的概率是p,則該事件發生的機率(此處機率指該事件發生概率與不發生概率之比)是p/1-p,對數機率是log(p/1-p),那麼,也就是說在邏輯斯諦迴歸模型中,輸出Y=1的對數機率是輸入x的線性函式,線性函式值越接近正無窮,概率值就越接近1,反之則越接近0.
• 似然估計:給定x的情況下引數θ是真實引數的可能性.
• 模型引數估計:對於給定的二分類訓練資料集,對數似然函式為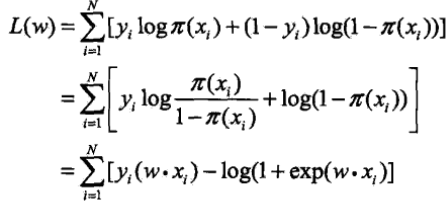,也就是損失函式.其中P(Y=1|x)=π(x),對L(w)求極大值,就可以得到w的估計值.問題變成了以對數似然函式為目標函式的最優化問題.

• 多項邏輯斯諦迴歸: 當問題是多分類問題時,可以作如下推廣:設Y有K類可能取值,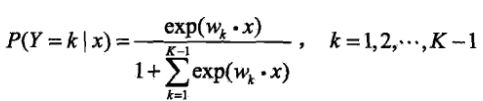,,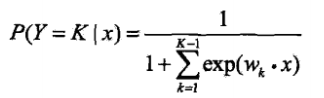實際上就是one-vs-all的思想,將其他所有類當作一個類,問題轉換為二分類問題.

• 最大熵原理:學習概率模型時,在所有可能的概率模型中,熵最大的模型是最好的模型.直觀地,最大熵原理認為模型首先要滿足已有的事實,即約束條件.在沒有更多資訊的情況下,那些不確定的部分都是"等可能的".

• 最大熵模型:給定訓練資料集,可以確定聯合分佈P(X,Y)的經驗分佈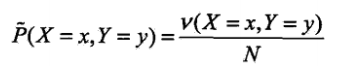和邊緣分佈P(X)的經驗分佈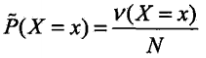,其中v表示頻數,N表示樣本容量.用特徵函式f(x,y)=1描述x與y滿足某一事實,可以得到特徵函式關於P(X,Y)的經驗分佈的期望值和關於模型P(Y|X)與P(X)的經驗分佈的期望值,假設兩者相等,就得到了約束條件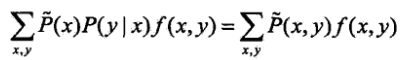.定義在條件概率分佈P(Y|X)上的條件熵為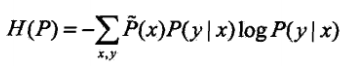,則條件熵最大的模型稱為最大熵模型.

• 最大熵模型的學習就是求解最大熵模型的過程.等價於約束最優化問題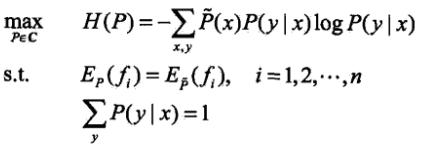,將求最大值問題改為等價的求最小值問題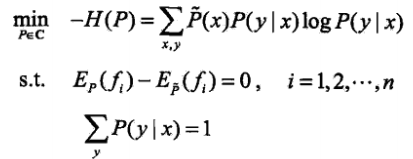.引入拉格朗日乘子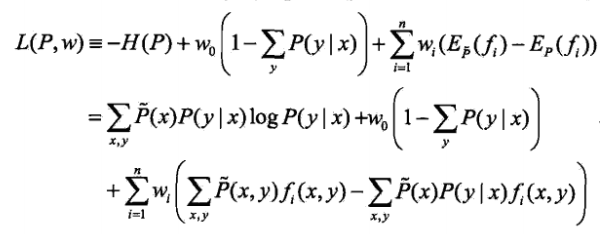將原始問題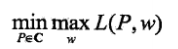轉換為無約束最優化的對偶問題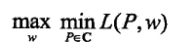.首先求解內部的極小化問題,即求L(P,W)對P(y|x)的偏導數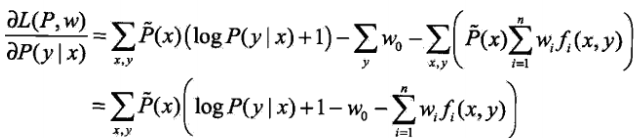,並令偏導數等於0,解得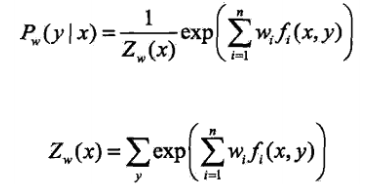.可以證明對偶函式等價於對數似然函式,那麼對偶函式極大化等價於最大熵模型的極大似然估計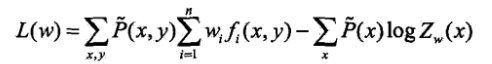.之後可以用最優化演算法求解得到w.

• 最大熵模型與邏輯斯諦迴歸模型有類似的形式,它們又稱為對數線性模型.模型學習就是在給定的訓練資料條件下對模型進行極大似然估計或正則化的極大似然估計.

• 演算法:似然函式是光滑的凸函式,因此多種最優化方法都適用.

1. 改進的迭代尺度法(IIS):假設當前的引數向量是w,如果能找到一種方法w->w+δ使對數似然函式值變大,就可以重複使用這一方法,直到找到最大值.
2. 邏輯斯諦迴歸常應用梯度下降法,牛頓法或擬牛頓法.

回到頂部

支援向量機

• 模型:支援向量機(SVM)是一種二類分類模型.它的基本模型是定義在特徵空間上的間隔最大的線性分類器.支援向量機還包括核技巧,使它成為實質上的非線性分類器.分離超平面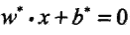,分類決策函式.
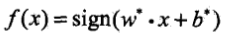• 策略:間隔最大化,可形式化為一個求解凸二次規劃的問題,也等價於正則化的合頁損失函式的最小化問題.
• 當訓練資料線性可分時,通過硬間隔最大化,學習出線性可分支援向量機.當訓練資料近似線性可分時,通過軟間隔最大化,學習出線性支援向量機.當訓練資料線性不可分時,通過使用核技巧及軟間隔最大化,學習非線性支援向量機.
• 核技巧:當輸入空間為歐式空間或離散集合,特徵空間為希爾伯特空間時,核函式表示將輸入從輸入空間對映到特徵空間得到的特徵向量之間的內積.通過核函式學習非線性支援向量機等價於在高維的特徵空間中學習線性支援向量機.這樣的方法稱為核技巧.
• 考慮一個二類分類問題,假設輸入空間與特徵空間為兩個不同的空間,輸入空間為歐氏空間或離散集合,特徵空間為歐氏空間或希爾伯特空間.支援向量機都將輸入對映為特徵向量,所以支援向量機的學習是在特徵空間進行的.
• 支援向量機的最優化問題一般通過對偶問題化為凸二次規劃問題求解,具體步驟是將等式約束條件代入優化目標,通過求偏導求得優化目標在不等式約束條件下的極值.
• 線性可分支援向量機:

1. 當訓練資料集線性可分時,存在無窮個分離超平面可將兩類資料正確分開.利用間隔最大化得到唯一最優分離超平面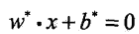和相應的分類決策函式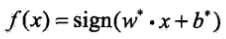稱為線性可分支援向量機.
2. 函式間隔:一般來說,一個點距離分離超平面的遠近可以表示分類預測的確信程度.在超平面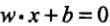確定的情況下,|wx+b|能夠相對地表示點x距離超平面的遠近,而wx+b與y的符號是否一致能夠表示分類是否正確.所以可用來表示分類的正確性及確信度,這就是函式間隔.注意到即使超平面不變,函式間隔仍會受w和b的絕對大小影響.

3. 幾何間隔:一般地,當樣本點被超平面正確分類時,點x與超平面的距離是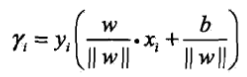,其中||w||是w的l2範數.這就是幾何間隔的定義.定義超平面關於訓練資料集T的幾何間隔為超平面關於T中所有樣本點的幾何間隔之最小值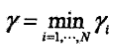.可知,當||w||=1時幾何間隔和函式間隔相等.

4. 硬間隔最大化:對線性可分的訓練集而言,這裡的間隔最大化又稱為硬間隔最大化.直觀解釋是對訓練集找到幾何間隔最大的超平面意味著以充分大的確信度對訓練資料進行分類.求最大間隔分離超平面即約束最優化問題: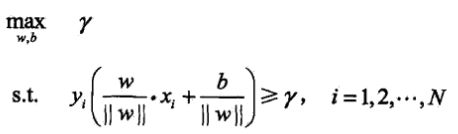,將幾何間隔用函式間隔表示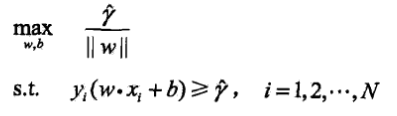,並且注意到函式間隔的取值並不影響最優化問題的解,不妨令函式間隔=1,並讓最大化1/||w||等價為最小化||w||^2/2,問題變為凸二次規劃問題.

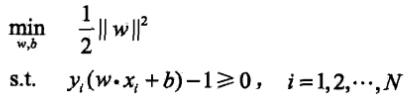5. 支援向量和間隔邊界:與分離超平面距離最近的樣本點的例項稱為支援向量.支援向量是使最優化問題中的約束條件等號成立的點.因此對y=+1的正例點和y=-1的負例點,支援向量分別在超平面H1:wx+b=+1和H2:wx+b=-1.H1和H2平行,兩者之間形成一條長帶,長帶的寬度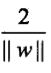稱為間隔,H1和H2稱為間隔邊界.在決定分離超平面時只有支援向量起作用,所以支援向量機是由很少的"重要的"訓練樣本確定的.由對偶問題同樣可以得到支援向量一定在間隔邊界上.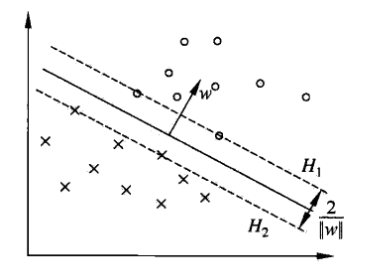

6. 對偶演算法: 引進拉格朗日乘子,定義拉格朗日函式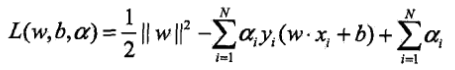,根據拉格朗日對偶性,原始問題的對偶問題是極大極小問題: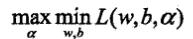.先求對w,b的極小值.將L(w,b,a)分別對w,b求偏導數並令其等於0,得,代入拉格朗日函式得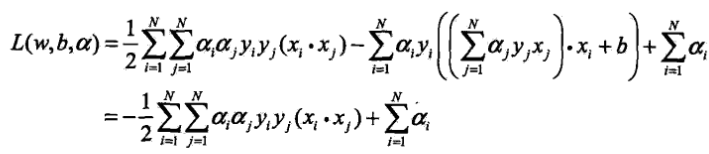

   ,這就是極小值.接下來對極小值求對a的極大,即是對偶問題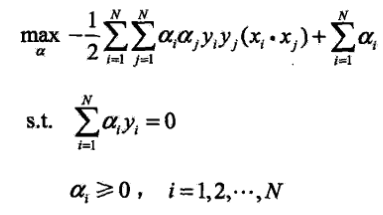.將求極大轉換為求極小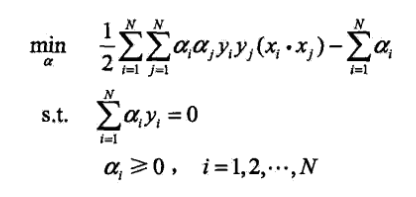.由KKT條件成立得到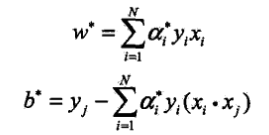,其中j為使aj*>0的下標之一.所以問題就變為求對偶問題的解a*,再求得原始問題的解w*,b*,從而得分離超平面及分類決策函式可以看出w*和b*都只依賴訓練資料中ai*>0的樣本點(xi,yi),這些例項點xi被稱為支援向量.

• 線性支援向量機:

1. 如果訓練資料是線性不可分的,那麼上述方法中的不等式約束並不能都成立,需要修改硬間隔最大化,使其成為軟間隔最大化.
2. 線性不可分意味著某些特異點不能滿足函式間隔大於等於1的約束條件,可以對每個樣本點引進一個鬆弛變數,使函式間隔加上鬆弛變數大於等於1,約束條件變為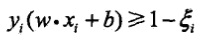,同時對每個鬆弛變數,支付一個代價,目標函式變為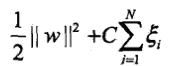,其中C>0稱為懲罰引數,C值越大對誤分類的懲罰也越大.新目標函式包含了兩層含義:使間隔儘量大,同時使誤分類點的個數儘量小.

3. 軟間隔最大化:學習問題變成如下凸二次規劃問題: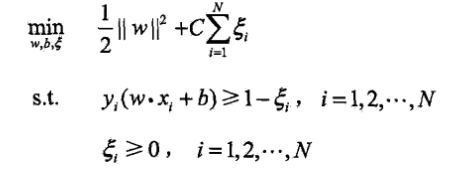,可以證明w的解是唯一的,但b的解存在一個區間.線性支援向量機包含線性可分支援向量機,因此適用性更廣.

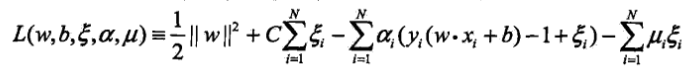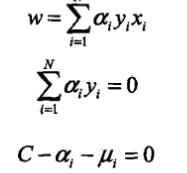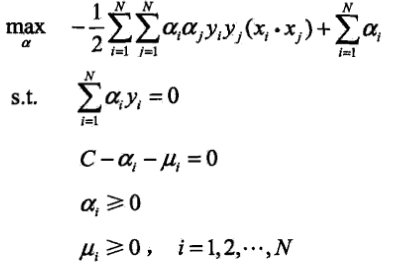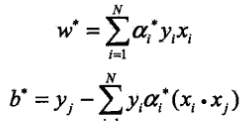4. 對偶演算法: 原始問題的對偶問題是,構造拉格朗日函式,先求對w,b,ξ的極小值,分別求偏導並令導數為0,得,代入原函式,再對極小值求a的極大值,得到,利用後三條約束消去μ,再將求極大轉換為求極小,得到對偶問題.由KKT條件成立可以得到,j是滿足0<aj*<C的下標之一.問題就變為選擇懲罰引數C>0,求得對偶問題(凸二次規劃問題)的最優解a*,代入計算w*和b*,求得分離超平面和分類決策函式.因為b的解並不唯一,所以實際計算b*時可以取所有樣本點上的平均值.

5. 支援向量:在線性不可分的情況下,將對應與ai*>0的樣本點(xi,yi)的例項點xi稱為支援向量.軟間隔的支援向量或者在間隔邊界上,或者在間隔邊界與分類超平面之間,或者再分離超平面誤分一側.

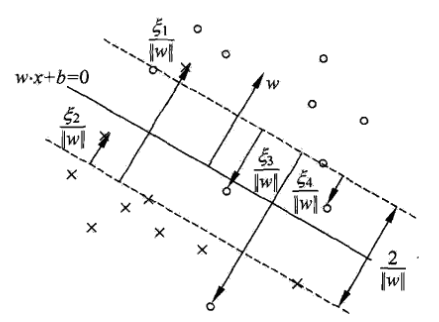
6. 合頁損失函式:可以認為是0-1損失函式的上界,而線性支援向量機可以認為是優化合頁損失函式構成的目標函式.

• 非線性支援向量機:

1. 如果分類問題是非線性的,就要使用非線性支援向量機.主要特點是使用核技巧.
2. 非線性分類問題:用線性分類方法求解非線性分類問題分為兩步:首先使用一個變換將原空間的資料對映到新空間,然後在新空間裡用線性分類學習方法從訓練資料中學習分類模型.
3. 核函式:設X是輸入空間(歐式空間的子集或離散集合),H為特徵空間(希爾伯特空間),一般是高維甚至無窮維的.如果存在一個從X到H的對映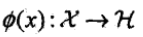使得對所有x,z屬於X,函式K(x,z)滿足條件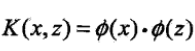,點乘代表內積,則稱K(x,z)為核函式.
4. 核技巧:基本思想是通過一個非線性變換將輸入空間對應於一個特徵空間,使得在輸入空間中的超曲面模型對應於特徵空間中的超平面模型(支援向量機).在學習和預測中只定義核函式K(x,z),而不顯式地定義對映函式.對於給定的核K(x,z),特徵空間和對映函式的取法並不唯一.注意到線上性支援向量機的對偶問題中,目標函式和決策函式都只涉及輸入例項與例項之間的內積,xi`xj可以用核函式K(xi,xj)=Ф(xi)`Ф(xj)來代替.當對映函式是非線性函式時,學習到的含有核函式的支援向量機是非線性分類模型.在實際應用中,往往依賴領域知識直接選擇核函式.
5. 正定核:通常所說的核函式是指正定核函式.只要滿足正定核的充要條件,那麼給定的函式K(x,z)就是正定核函式.設K是定義在X*X上的對稱函式,如果任意xi屬於X,K(x,z)對應的Gram矩陣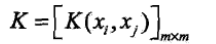是半正定矩陣,則稱K(x,z)是正定核.這一定義在構造核函式時很有用,但要驗證一個具體函式是否為正定核函式並不容易,所以在實際問題中往往應用已有的核函式.
6. 演算法:選取適當的核函式K(x,z)和適當的引數C,將線性支援向量機對偶形式中的內積換成核函式,構造並求解最優化問題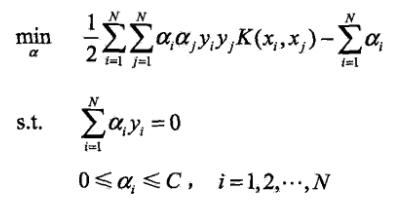,選擇最優解a*的一個正分量0<aj*<C計算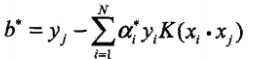,構造決策函式.

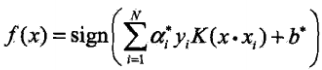• 常用核函式:

1. 多項式核函式(polynomial kernel function):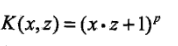,對應的支援向量機是一個p次多項式分類器,分類決策函式為.

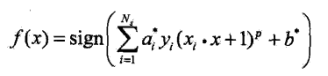2. 高斯核函式(Gaussian krenel function):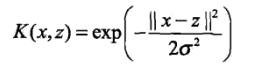,對應的支援向量機是高斯徑向基函式(RBF)分類器.分類決策函式為.

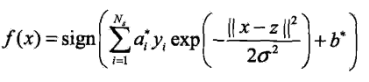3. 字串核函式(string kernel function): 核函式不僅可以定義在歐氏空間上,還可以定義在離散資料的集合上.字串核函式給出了字串中長度等於n的所有子串組成的特徵向量的餘弦相似度.

• 序列最小最優化(SMO)演算法:

1. SMO是一種快速求解凸二次規劃問題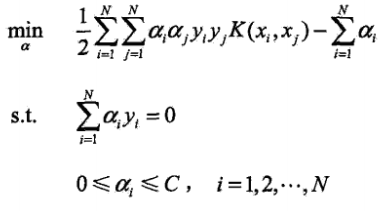的演算法.基本思路是:如果所有變數都滿足此優化問題的KKT條件,那麼解就得到了.否則,選擇兩個變數,固定其他變數,針對這兩個變數構建一個二次規劃問題.不斷地將原問題分解為子問題並對子問題求解,就可以求解原問題.注意子問題兩個變數中只有一個是自由變數,另一個由等式約束確定.
2. 兩個變數二次規劃的求解方法:假設選擇的兩個變數是a1,a2,其他變數是固定的,於是得到子問題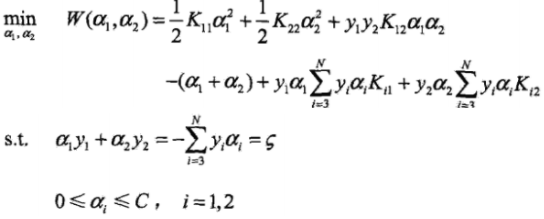,ε是常數,目標函式式省略了不含a1,a2的常數項.考慮不等式約束和等式約束,要求的是目標函式在一條平行於對角線的線段上的最優值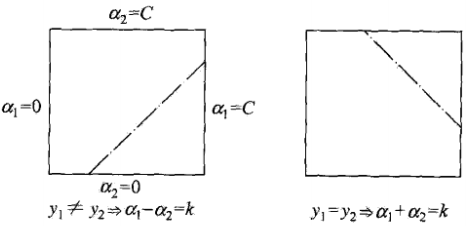,問題變為單變數的最優化問題.假設初始可行解為aold,最優解為anew,考慮沿著約束方向未經剪輯的最優解anew,unc(即未考慮不等式約束).對該問題求偏導數,並令導數為0,代入原式,令,得到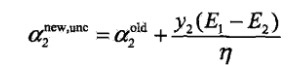,經剪輯後a2的解是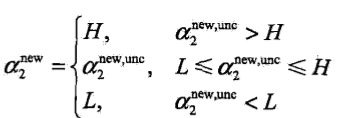,L與H是a2new所在的對角線段端點的界.並解得.
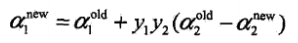3. 變數的選擇方法:在每個子問題中選擇兩個變數優化,其中至少一個變數是違反KKT條件的.第一個變數的選取標準是違反KKT條件最嚴重的樣本點,第二個變數的選取標準是希望能使該變數有足夠大的變化,一般可以選取使對應的|E1-E2|最大的點.在每次選取完點後,更新閾值b和差值Ei.

回到頂部

提升方法

• 提升(boosting)是一種常用的統計學習方法,是整合學習的一種.它通過改變訓練樣本的權重(概率分佈),學習多個弱分類器(基本分類器),並將這些分類器線性組合來構成一個強分類器提高分類的效能.
• AdaBoost:

1. AdaBoost提高那些被前一輪弱分類器錯誤分類樣本的權值,而降低那些被正確分類樣本的權值.然後採取加權多數表決的方法組合弱分類器.
2. 演算法:首先假設訓練資料集具有均勻的權值分佈D1,