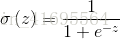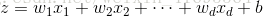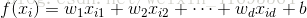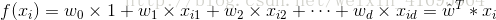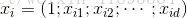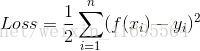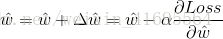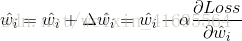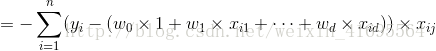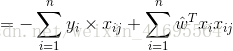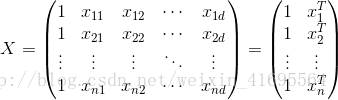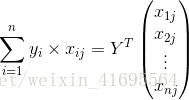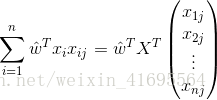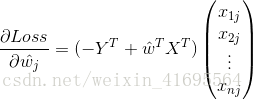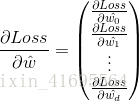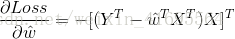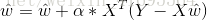機器學習筆記(三)——Logistic Regression 的原理以及程式碼實現
假設現在有一些資料點,我們用一條直線對這些點進行擬合(該線稱為最佳擬合直線),這個擬合過程就稱作迴歸。利用Logistic 迴歸進行分類的主要思想是:根據現有資料對分類邊界線建立迴歸公式,以此進行分類。這裡的“ 迴歸“一詞源於最佳擬合,表示要找到最佳擬合引數集,其背後的數學分析將在下面介紹。訓練分類器的做法就是尋找最佳擬合引數,使用的是梯度下降法,本文首先闡述Logistic 迴歸的定義,然後推導迴歸係數的迭代公式,最後給出一個Logistic 迴歸的例項,使用python 3.6編寫程式碼,根據腫瘤的形狀資料來預測腫瘤的良惡性。
一、Sigmoid函式的介紹
Logistic Regression是線性迴歸,但最終是用作分類器:它從樣本集中學習擬合引數,將目標值擬合到[0,1]之間,然後對目標值進行離散化,實現分類。
為什麼叫Logistic呢?因為它使用了Logisitic函式(又稱為Sigmoid函式),這個Sigmoid函式將分類任務的真實標記和線性迴歸模型的預測值聯絡起來。Sigmoid函式具體的計算公式如下:
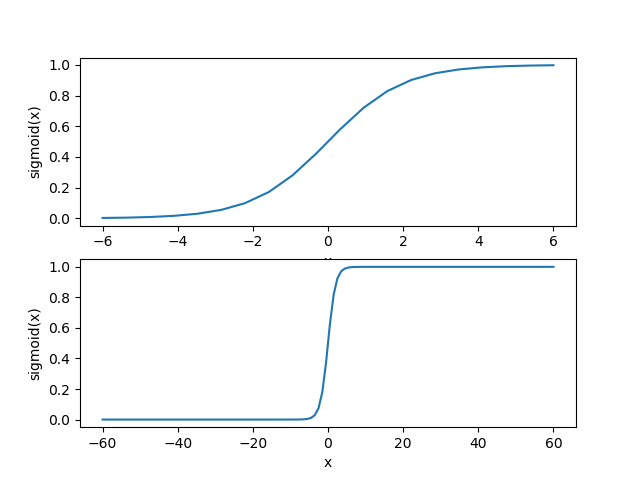
首先我們來看一下Sigmoid函式在不同座標尺度下的兩條曲線圖,下面是繪製曲線圖的python程式碼:
import numpy as np import matplotlib.pyplot as plt def sigmoid( inx ): """ 這是sigmoid函式 """ return 1.0/(1+np.exp(-inx)) x_value = np.linspace(-6,6,20) y_value = sigmoid( x_value ) xx_value = np.linspace(-60,60,120) yy_value = sigmoid( xx_value ) #numpy模組中的linspace()函式與arange()函式非常相似。它的前兩個引數同樣是用來指定序列的起始和結尾, #但是第三個引數不再表示相鄰兩個數字之間的距離,而是用來指定我們想把由開頭和結尾兩個數字所指定的範圍分成幾個部分。 fig = plt.figure() ax1 = fig.add_subplot(211) ax1.plot( x_value,y_value ) ax1.set_xlabel('x') ax1.set_ylabel('sigmoid(x)') ax2 = fig.add_subplot(212) ax2.plot( xx_value,yy_value ) ax2.set_xlabel('x') ax2.set_ylabel('sigmoid(x)') plt.show()
得到兩種座標尺度下的Sigmoid函式圖,如下所示,其中上圖的橫座標為-6到6,這時的曲線變化較為平滑;下圖橫座標的尺度足夠大,可以看到,在x=0點處Sigmoid函式看起來很像單位階躍函式。而這種類似於階躍函式的效果正是我們想要的,考慮二分類任務,其輸出標記為0和1,而Sigmoid函式將z值轉化為一個接近0或1的y值,並且其輸出值在z = 0附近變化很陡。
Sigmoid函式的輸入記為z,暫且又下面公式表出:
其中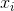
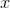
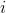
為了使得分類器儘可能地精確,我們需要找到最佳引數(係數),然而,為了找到最佳引數(係數),需要用到最優化理論的一些知識。
二、線性迴歸的基礎
給定包含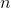
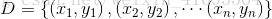
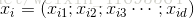
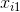
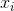
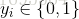
線性模型試圖學得一個通過屬性的線性組合來進行預測的函式,即
一般用向量形式寫出
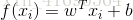
其中
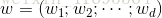
為了便於討論,我們把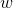
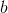
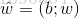
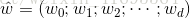
其中
如何確定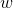
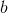
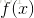
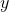
顯然此公式是二次方程,有最小值,當它取最小值得時候,所對應的


三、梯度下降法求解優化問題
梯度下降法基於的思想是;要找到某函式的最小值,最好的方式就是沿著該函式的梯度方向的反方向搜尋。
其步驟是,先隨機給


其中,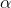
我們先來求解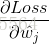
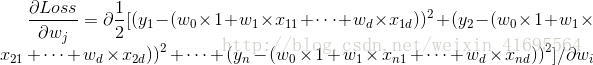
前面我們為了便於討論,已經把
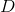
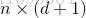
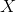
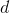

再把標記也寫出向量形式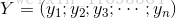
同理,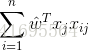
所以,誤差的一階偏導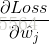
綜上所述,我們把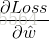
結合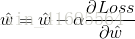
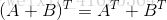


四、Logistic Regression的程式碼實現
上一節我們用梯度下降法推匯出
部分資料如下所示:
接下來我們編寫兩個載入資料集的函式,一個用來載入訓練集,另一個用來載入測試集,程式碼如下所示:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['simHei']
#這句話用來設定 matplotlib.pyplot模組繪製的圖中正常顯示中文字型
plt.rcParams['axes.unicode_minus']=False
#這句話用來設定 matplotlib.pyplot模組繪製的圖中正常顯示負號
###################################
##### theme:邏輯迴歸實戰 #####
#### author:行歌 #######
#### time:2018.3.11 ######
################################
def loadTrainDataSet(file_name):
"""
此函式用來向csv格式的檔案中載入訓練資料,並以陣列的形式輸出訓練集和類別標籤。
輸入: file_name1是訓練集所在的相對地址
輸出: trainDateArr是訓練資料集(524*3的陣列形式)
trainLabelArr是訓練集的類別標籤(1*524的陣列形式)
"""
trainData = pd.read_csv(file_name)
trainDate_1 = trainData[['Clump Thickness','Cell Size']].values
trainLabelArr = trainData[['Type']].values.ravel()
bias_item_train = np.mat([1.0]*trainDate_1.shape[0]).T
trainDateArr = np.hstack((bias_item_train,trainDate_1)).A
return trainDateArr, trainLabelArr
def loadtestDataSet(file_name):
"""
此函式用來向csv格式的檔案中載入測試資料,並以陣列的形式輸出測試集和類別標籤。
輸入: file_name1是測試集所在的相對地址
輸出: testDateArr是測試資料集(175*2的陣列形式)
testLabelArr是測試集的類別標籤(1*175的陣列形式)
"""
testData = pd.read_csv(file_name)
testDateArr_1 = testData[['Clump Thickness','Cell Size']].values
testLabelArr = testData[['Type']].values.ravel()
bias_item_test = np.mat([1.0] * testDateArr_1.shape[0]).T
testDateArr = np.hstack(( bias_item_test,testDateArr_1)).A
return testDateArr, testLabelArr
載入完資料我們列印一下訓練集和類別標籤,如下所示:
訓練集陣列的第一列全為1.0,它們對應線性迴歸方程中的偏置項,前面我們講過。
接下我們編寫函式來根據輸入的訓練集來計算迴歸係數,程式碼如下:
def sigmoid( inx ):
"""
這是sigmoid函式
"""
return 1.0/(1+np.exp(-inx))
def calculate_regression_coefficient( DateArr, LabelArr ):
"""
此函式用來計算線性迴歸中的迴歸係數
輸入: DateArr是陣列形式的樣本集
LabelArr是樣本集對應的類別標籤
輸出: weight_vector是迴歸係數向量
"""
m, n = DateArr.shape
LabelArr = LabelArr.reshape(m,1)
alpha = 0.001
max_iterations = 500
weight_vector = np.ones((n,1))
for i in range( max_iterations ):
h = sigmoid( np.dot(DateArr, weight_vector) )
error = ( LabelArr - h )
weight_vector = weight_vector + alpha * np.dot(DateArr.T, error)
return weight_vector將訓練集代入其中,可以得到迴歸係數如下所示:
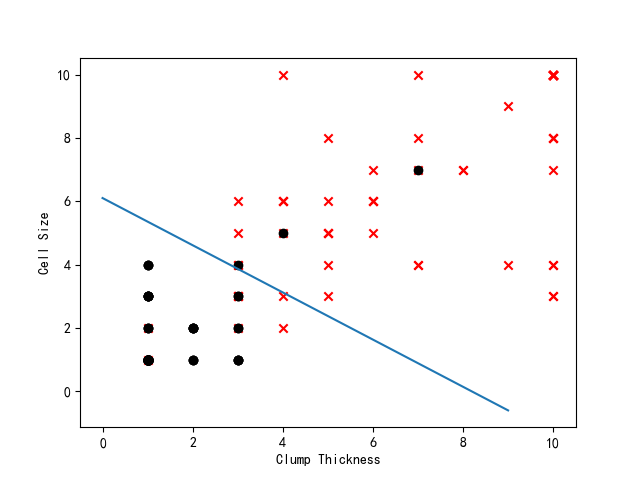
現在我們已經得到迴歸係數,也就意味著我們得到邏輯迴歸模型了,於是,我們編寫函式預測測試集樣本的類別,並與真實類別相比較,計算出錯誤率或者正確率,同時將測試集樣本在散點圖中展出,根據迴歸係數,畫出不同類別資料之間的分隔線。程式碼如下所示:
def classifyVector(inx,weight_vector ):
"""
此函式以迴歸係數和特徵向量作為輸入來計算對應的Sigmoid值。如果Sigmoid值大於0.5,則函式返回1,否則返回0
"""
prob = sigmoid( np.sum(inx * weight_vector))
if prob > 0.5:
return 1.0
else:
return 0.0
def calculata_errorRate( testDateArr, testLabelArr, weight_vector ):
"""
這個函式根據測試集的樣本,計算分類錯誤率
"""
prob_Arr = sigmoid(np.dot( testDateArr,weight_vector ))
label_result = np.zeros((prob_Arr.shape[0],1))
label_result[np.nonzero(prob_Arr > 0.5)[0]] = 1.0
total_error = 0.0
for i in range(len(label_result)):
if label_result[i] != testLabelArr[i]:
total_error += 1
errorRate = total_error/ len(label_result)
return errorRate
def draw_testDate_scatterGraph(testDateArr, testLabelArr,weight_vector):
"""
此函式首先將測試資料集按照類別劃分為正類和負類兩個資料集,然後以散點圖的形式將它們展現出來。
輸入: testDateArr 測試資料集(175*2的陣列形式)
testLabelArr 測試資料集對應的類別標籤(1*175的陣列形式)
輸出: 散點圖
"""
positive_index = np.nonzero( testLabelArr ==1 )
testDateArr_positive = testDateArr[positive_index]
negative_index = np.nonzero( testLabelArr == 0 )
testDateArr_negative = testDateArr[negative_index]
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(testDateArr_positive[:,1], testDateArr_positive[:,2], marker='x', c='red')
ax.scatter(testDateArr_negative[:, 1], testDateArr_negative[:, 2], marker='o', c='black')
ax.plot(np.arange(0,10),(-np.arange(0,10)*weight_vector[1]-weight_vector[0])/weight_vector[2])
plt.xlabel('Clump Thickness', fontsize=10)
plt.ylabel('Cell Size', fontsize=10)
plt.show()
接下來,我們編寫主函式:
if __name__ == '__main__':
trainDateArr, trainLabelArr = loadTrainDataSet('breast-cancer-train.csv')
testDateArr, testLabelArr = loadtestDataSet('breast-cancer-test.csv')
weight_vector = calculate_regression_coefficient( trainDateArr, trainLabelArr )
draw_testDate_scatterGraph(testDateArr,testLabelArr,weight_vector)
errorRate = calculata_errorRate( testDateArr, testLabelArr, weight_vector )
print('錯誤率:%f' % errorRate)
print('正確率:%f' % (1-errorRate))
通過執行,我們得到結果如下:
正確率93%,這已經很不錯啦!
至此,我們的 Logistic Regression就學習完畢啦!
參考文獻:
[1] 周志華 《機器學習》
[2] Peter Harrington 《機器學習實戰》
相關推薦
機器學習筆記(三)——Logistic Regression 的原理以及程式碼實現
假設現在有一些資料點,我們用一條直線對這些點進行擬合(該線稱為最佳擬合直線),這個擬合過程就稱作迴歸。利用Logistic 迴歸進行分類的主要思想是:根據現有資料對分類邊界線建立迴歸公式,以此進行分類。這裡的“ 迴歸“一詞源於最佳擬合,表示要找到最佳擬合引數集
機器學習筆記(三)Logistic迴歸模型
Logistic迴歸模型 1. 模型簡介: 線性迴歸往往並不能很好地解決分類問題,所以我們引出Logistic迴歸演算法,演算法的輸出值或者說預測值一直介於0和1,雖然演算法的名字有“迴歸”二字,但實際上Logistic迴歸是一種分類演算法(classification y = 0 or 1)。 Log
機器學習筆記(四)Logistic迴歸實現及正則化
一、Logistic迴歸實現 (一)特徵值較少的情況 1. 實驗資料 吳恩達《機器學習》第二課時作業提供資料1。判斷一個學生能否被一個大學錄取,給出的資料集為學生兩門課的成績和是否被錄取,通過這些資料來預測一個學生能否被錄取。 2. 分類結果評估 橫縱軸(特徵)為學生兩門課成績,可以在圖
機器學習筆記(三):線性迴歸大解剖(原理部分)
進入機器學習,線性迴歸自然就是一道開胃菜。雖說簡單,但對於入門來說還是有些難度的。程式碼部分見下一篇,程式碼對於程式設計師還是能能夠幫助理解那些公式的。 (本文用的一些課件來自唐宇迪的機器學習,大家可以取網易雲課堂看他的視訊,很棒) 1.線性迴歸的一些要點 先說
機器學習筆記(三):線性迴歸大解剖(程式碼部分)
這裡,讓我手把手教你如何用邏輯迴歸分析資料 根據學生分數預測是否錄取: #必備3個庫 import numpy as np import pandas as pd import matplotlib.pyplot as plt 讓我們讀入資料: import
機器學習筆記(三) 第三章 線性模型
3.1 基本形式 樣本x由d個屬性描述 x= (x1; x2;…; xd), 線性模型試圖學得一個通過屬性的線性組合來進行預測的函式: 向量形式: w和b學得之後,模型就得以確定. 3.2 線性迴歸 線性迴歸試圖學得 為確定w,b,學習到泛化效能最好的模型
機器學習筆記(三):決策樹
決策樹(decision tree)是機器學習中最常見的方法之一,本文主要對決策樹的定義,生成與修剪以及經典的決策樹生成演算法進行簡要介紹。目錄如下 一、什麼是決策樹 二、決策樹的生成 三、決策樹的修剪 四、一些經典的決策樹生成演算法 一、什麼是決策樹 顧名
機器學習筆記(四)Logistic迴歸
我們都知道,如果預測值y是個連續的值,我們通常用迴歸的方法去預測,但如果預測值y是個離散的值,也就是所謂的分類問題,用線性迴歸肯定是不合理的,因為你預測的值沒有一個合理的解釋啊。比如對於二分類問題,我
機器學習筆記(三)——正則化最小二乘法
一. 模型的泛化與過擬合 在上一節中,我們的預測函式為: f(x;ω)=ωTx 其中, x=[x1],ω=[ω1ω0] 上述稱為線性模型,我們也可以將x擴充套件為: x=⎡⎣⎢⎢⎢⎢⎢⎢⎢xn⋮x2x1⎤⎦⎥⎥⎥⎥⎥⎥⎥,ω=⎡⎣⎢⎢⎢⎢⎢⎢⎢ωn⋮
機器學習筆記(4)Logistic回歸
可能性 相同 模擬 我們 inline alt 最小 cas 離散 模型介紹 對於分類問題,其得到的結果值是離散的,所以通常情況下,不適合使用線性回歸方法進行模擬。 所以提出Logistic回歸模型。 其假設函數如下: \[ h_θ(x)=g(θ^Tx) \] 函數g定義如
Mybatis 學習筆記(三)——使用Mapper代理的方式實現資料增刪改查
一、介紹 Mapper代理的方式只需要程式設計師編寫 Mapper.xml 檔案及 Mapper介面。 本文是基於上一篇文章:Mybatis 學習筆記——原生DAO實現資料增刪改查,所以接下來的內容是以其為基礎的,如果有什麼不懂的請留言或檢視上一篇。所
SQLite學習筆記(十)-- 事務基本概念和程式碼實現(C++實現)
1.事務基本概念 什麼是事務? 事務是使用者定義的一些列資料操作,這些操作是一個完整的不可分的工作單元。一個事務要麼全部執行,要麼全部不執行。 檢視案例 例如銀行的轉賬操作,張三向李四轉賬1000元。該事務包含以下兩個操作: 1.張三賬戶上扣除1000
CS229機器學習個人筆記(3)——Logistic Regression+Regularization
1.Classification Logistic Regression其實就是Classification,但是由於歷史原因名字被記作了邏輯迴歸。它與線性迴歸的區別在於 hθ(x) h_\theta(x)被限制在了0與1之間,這是通過下面的S函式(Sigmoi
斯坦福Andrew Ng---機器學習筆記(二):Logistic Regression(邏輯迴歸)
內容提要 這篇部落格的主要內容有: - 介紹欠擬合和過擬合的概念 - 從概率的角度解釋上一篇部落格中評價函式J(θ)” role=”presentation” style=”position: relative;”>J(θ)J(θ)為什麼用最
《自己動手寫java虛擬機器》學習筆記(三)-----搜尋class檔案(go)
專案地址:https://github.com/gongxianshengjiadexiaohuihui 我們都知道,.java檔案編譯後會形成.class檔案,然後class檔案會被載入到虛擬機器中,被我們使用,那麼虛擬機器如何從那裡尋找這些class檔案呢,jav
機器學習(西瓜書)學習筆記(三)---------決策樹
1、基本流程 決策樹通常從一個最基本的問題出發,通過這個判定問題來對某個“屬性”進行“測試”,根據測試的結果來決定匯出結論還是匯出進一步的判定問題,當然,這個判定範圍是在上次決策結果的限定範圍之內的。 出發點
python3.5《機器學習實戰》學習筆記(三):k近鄰演算法scikit-learn實戰手寫體識別
轉載請註明作者和出處:http://blog.csdn.net/u013829973 系統版本:window 7 (64bit) 我的GitHub:https://github.com/weepon python版本:python 3.5 IDE:Spy
Python3《機器學習實戰》學習筆記(三):決策樹實戰篇之為自己配個隱形眼鏡
轉載請註明作者和出處: http://blog.csdn.net/c406495762 執行平臺: Windows Python版本: Python3.x IDE: Sublime text3 一 前言 上篇文章,Python3《
google機器學習框架tensorflow學習筆記(三)
降低損失:迭代法 迭代學習其實就是一種反饋的結果,有點類似於猜數遊戲,首先你隨便猜一個數,對方告訴你大了還是小了,接著你根據對方提供的資訊進行調整,繼續往正確的方向猜測,如此往復,你通常會越來越接近要猜的數。 這個遊戲真正棘手的地方在於儘可能高效地找到最佳模型。 下圖
機器學習(周志華版)學習筆記(三)歸納偏好
定義:機器學習演算法在學習過程中對某種型別假設的偏好。 每種演算法必有其歸納偏好,否則它將被假設空間中看似在訓練集上“等效”的假設所迷惑,無法產生確定的學習結果。 例子理解: 編號 色澤 根蒂 敲聲 好瓜 1 青綠 蜷縮 濁響 是