一，分類問題（又叫做預測問題，預測的物件是數值型別）

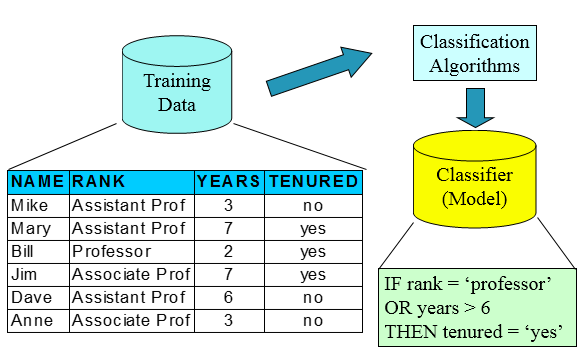
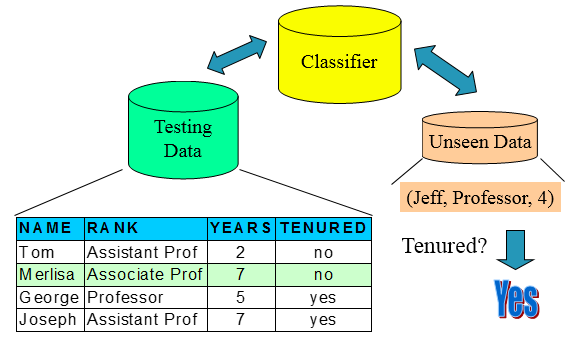
　　訓練集（用來構建模型，擬合模型，可以訓練出很多個模型）——>使用模型：測試集（僅僅一次使用，評估模型泛化的效能），驗證集（進行模型的選擇選擇特徵，調參，防止過擬合，多次使用，以不斷調參），這些都是已知table的

　　分類問題的本質是，根據一些屬性去分標籤屬性

 二，決策樹

　　根據輸入，從樹的根最後在樹裡面走一遍到輸出的葉子節點，得到分類結果。分類的目的是讓不確定性消失，使熵下降最快，使子節點的純度最高。

• 　　步鄹：（1）將所有資料都放在根節點，

　　　　　（2）選擇一個特徵進行分解出子節點

　　　　　（3）在子節點上判斷是否不再分裂，如果不再分裂則直接給出這個子節點的分類結果（這個子節點的多數table為這個節點的輸出table），否則繼續選擇一個特徵進行分解（即到第二步）

• 　　演算法的核心：最優分裂特徵（節點）的選取；分裂成幾類；什麼時候停止分裂。
• 　　分裂特徵的選取：ID3演算法，C4.5演算法（可以用來決定分裂成幾類，即最優分裂值的選取），CART樹

　　（1）ID3：使資訊增益最大。（熵下降最快）

　　父節點的熵-子節點的熵

    InfoA是分類之後的，分別求各子節點的熵，再乘上各子節點概率。

　　注意：根節點計算的時候，Info(D)是算沒有任何條件的分類結果的概率

 （2）C4.5：使資訊增益率最大（減弱ID3的缺點，ID3偏向於選擇多分支，因為多分支意味著純度高）

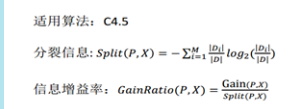
分母 是把子節點看成整體，算出分裂成子節點之後的整體的熵。

 例題：

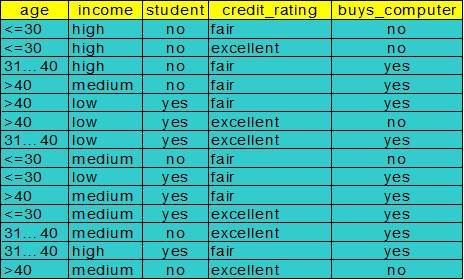
要分類的標籤table：buys_computer：no or yes

選取第一個節點：

Info income(D)=4/14*I(2,2)+6/14*I(3,1)+4/14*i(3,1)

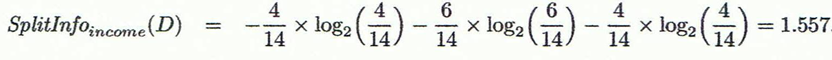
(3)CARt樹

　　基尼係數：衡量子節點的純度，基尼係數越小，純度越高（其實和熵的意思差不多）

　　分成子節點的GINI係數，是要分別求GINI再對概率的加權求和。

迴歸樹（輸入是連續值）：

　　先劃分節點，將資料集分裂：在整個區間內取一個點，將區間分為兩部分，使損失函式最小。

參考：https://www.cnblogs.com/fionacai/p/5894142.html

https://www.cnblogs.com/wenyi1992/p/7685131.html