HDU 1978 How many ways(記憶化搜尋)
阿新 • • 發佈:2018-11-27
How many ways
Time Limit: 3000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 6661 Accepted Submission(s): 3865 Problem Description 這是一個簡單的生存遊戲,你控制一個機器人從一個棋盤的起始點(1,1)走到棋盤的終點(n,m)。遊戲的規則描述如下:1.機器人一開始在棋盤的起始點並有起始點所標有的能量。 2.機器人只能向右或者向下走,並且每走一步消耗一單位能量。 3.機器人不能在原地停留。 4.當機器人選擇了一條可行路徑後,當他走到這條路徑的終點時,他將只有終點所標記的能量。
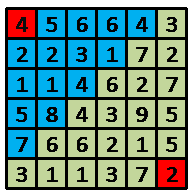
如上圖,機器人一開始在(1,1)點,並擁有4單位能量,藍色方塊表示他所能到達的點,如果他在這次路徑選擇中選擇的終點是(2,4) 點,當他到達(2,4)點時將擁有1單位的能量,並開始下一次路徑選擇,直到到達(6,6)點。 我們的問題是機器人有多少種方式從起點走到終點。這可能是一個很大的數,輸出的結果對10000取模。
Input 第一行輸入一個整數T,表示資料的組數。
Output 對於每一組資料輸出方式總數對10000取模的結果.
Sample Input 1 6 6 4 5 6 6 4 3 2 2 3 1 7 2 1 1 4 6 2 7 5 8 4 3 9 5 7 6 6 2 1 5 3 1 1 3 7 2
Sample Output 3948
|
AC_CODE:
#include <iostream> #include <cstring> using namespace std; int a[105][105]; int dp[105][105]; int n,m; const int MOD=10000; bool OK(int x,int y) { if(x<1||x>n||y<1||y>m) return false; return true; } int DFS(int x,int y) { if(dp[x][y]>=0) return dp[x][y]; dp[x][y]=0; for(int i=0;i<=a[x][y];i++) { for(int j=0;i+j<=a[x][y];j++) { if(OK(x+i,y+j)) { dp[x][y]=(dp[x][y]+DFS(x+i,y+j))%MOD; } } } return dp[x][y]; } int main() { int t; cin>>t; while(t--) { cin>>n>>m; for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) cin>>a[i][j]; memset(dp,-1,sizeof(dp)); dp[n][m]=1; cout<<DFS(1,1)<<endl; } return 0; }