Segment 0 回顧

• Object-space normal map和tangent-space normal map區別。
  Object-space normal map裡面的法線向量值是參考object座標系搞出來的，而tangent space normal map裡面的法線向量值是先在高模Obj對應的低模Obj上面每一個點建立一個座標系，這個座標系叫做tangent space（一般Z軸就是低模上這個點的法線，X，Y軸分別是uv座標的方向），之後，把高摸上每一點的法線向量轉換到這個tangent space裡面，這樣形成的一個map就是tangent space normal map。這樣看來tangent space normal map裡面每一個點本質上記錄的其實是一個偏差，也就是該點處低模法線方向和高模法線方向之間的差別（請注意，這只是個比喻，方便理解而已，實際上記錄的根本不是兩個向量差，因為如果記錄的是向量差，那麼整個概念還是一樣的，但是演算法卻差別很大了。真正的tangent space normal map是將高模的法線值存進低模的tangent座標系當中，這樣在拿tangent space normal map去蒙皮的時候，只需要在所需蒙皮的物體的每一個點的tangent space裡面把原來的法線值刪除，更換成tangent space normal map的值就好了）

  
  下圖是obj-space normal map和tangent space normal map的實際樣子。

  

• 明白了Obj-space normal map和tangent space normal map之後，總要知道為何搞了這兩種吧，於是看了很多文章敘說Object space normal 和 tangent space 優缺點之類的，大家都說一些什麼Obj的效率高、tangent的適用廣。看得不甚了了，覺得都是結論，我自己總是沒抓住實質，直到自己親手用筆畫了畫才豁然開朗。

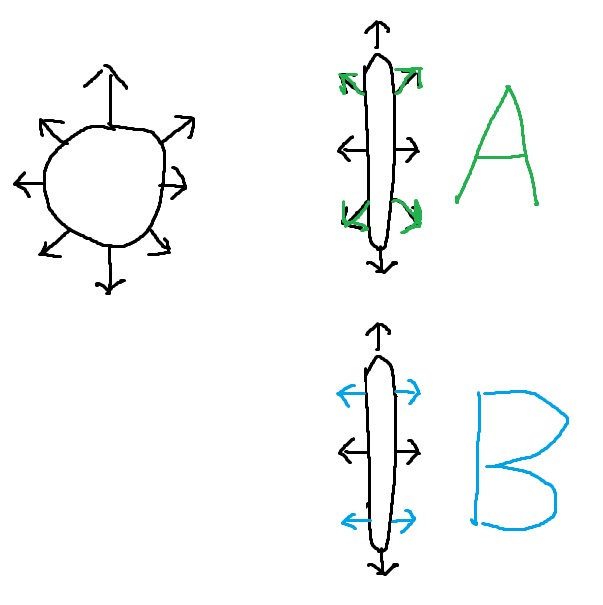
  請看下圖
  

  在這個圖裡面，我們有一個原始的球。從這個球上面當然能扒出一張法線貼圖（這裡為了簡便，我預設這個球每個頂點的法線方向是正常的，也就是說垂直於每個頂點的），你可以扒一張Obj space normal map，也可以扒一張tangent space normal map，此時沒啥影響。

  接下來我們要用這兩張normal map去貼我其他專案裡面的物體。

  如果，此時貼的還是一個球，那麼Obj space normal map和 tangent space normal map都可以，不管我這個新的球是旋轉過、平移過、縮放過（一般我們所謂的旋轉、平移、縮放都是在world space做的。但是此處、對於這個球來說，我們講的是在它自己的Obj space裡面做旋轉、平移、縮放），球被貼完圖之後，看起來還是原來的樣子，並沒有什麼區別。

  接下來，刺激的事情發生了，假設我把這個球做了變形(deform)，變成了上圖右側的那種棍子狀。那麼這時候用Obj space normal map和tangent space normal map分別去貼這個棍子的時候，毫無疑問貼完之後會有不同。會有啥不同呢？為了方便，我們就預設Obj space的原點就是物體的質心吧，如果我們用Obj space normal map去貼棍子，這樣棍子上面每一個點的法線值都會被替換成Obj space normal map上面對應點的法線值（舉個例子，左上角那個點的法線方向指向左上方，貼到棍子上去之後，毫無疑問在棍子上面對應點的法線就被替換了，棍子上的法線就指向了左上方），貼完之後樣子就是圖裡面的A；如果我們用tangent space normal map去貼，就會貼成B圖。因為在用tangent space normal map貼的時候，我們是在棍子上面每一個點的tangent space裡面貼的，而不是在棍子的Obj space裡面貼的。還是拿左上角那個點舉例，首先取得棍子上左上角那個點的tangent座標系（很好取，Z軸 為棍子模型左上角這個點的模型法線法線，X,Y分別為uv方向），取完座標系之後自然就能得知在這個點的tangent座標系裡面它的原始法線方向是(0,0,1)，接下來就根據uv座標去找tangent space normal map裡面對應點的值，很容易就可看出此時tangent space normal map裡面對應的值就是(0,0,1)（因為光滑球面麼，法線一定是垂直的呀），然後就拿tangent space normal map裡面這個值替換掉之前的原始值，大功告成，這就是B

  好了，從人類的本能來看，一個金屬球被捏成棍子之後，反光是啥感覺？絕對不可能是A，一定就是B。這符合人類直覺。如果我們故意搞成A的話，一個光源照在棍子上之後，我們肉眼看到的就是一個圓形的光斑，這明顯不符合現實；而做成B的話，一個光源照在棍子上之後是一條豎著的光斑，真實的很（想象一下在太陽下面拿一個金屬棍和金屬球，他們的反光是啥感覺）。
  所以對於變形(deform）來說，明顯tangent space normal map好。同理，當搞什麼uv_texture動畫時（水流動，岩漿流動） ，那必須是tangent space好用啊。
  也有人談過說tangent space normal map在變形變的厲害的地方，譬如說一個尖角處會有縫合問題，這個就不是我現在能操弄的了，要等待未來繼續學習的結果。