非引數統計檢驗
阿新 • • 發佈:2018-11-28
非引數統計的方法用於總體分佈未知的情形,其目的在於檢驗一個變數的分佈在不同組中是否具有相同的位置引數。
NPAR1WAY語句
功能
格式:
proc npar1way data=資料集名 [選項];
by 變數名;
class 變數名;
var 變數名;
run;
注:
proc的選項:
i.wilcoxon:指定使用Wilcoxon秩和分析方法;
ii.noprint:結果輸出視窗不顯示計算結果;
例
單個樣本的非引數檢驗
此情形使用Univariate過程。
目的: 檢驗某個樣本均值是否等於特定值。
某產品標註的淨含量為1kg,現對該產品進行抽樣統計分析,試判斷該產品重量是否與標註一致?
程式碼:
data test; /*建立資料集*/
input x @@;
cards;
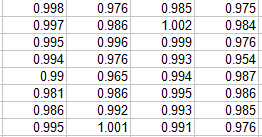
0.998 0.997 0.995 0.994 0.990 0.981 0.986 0.995
0.976 0.986 0.996 0.976 0.965 0.986 0.992 1.001
0.985 1.002 0.999 0.993 0.994 0.995 0.993 0.991
0.975 0.984 0.976 0.954 0.987 0.986 0.985 0.976
;
run;
proc univariate data=test mu0=1; /*設定mu0為1,檢驗其*均值是否為1/
var x;
run;
結果:
給出了一些基本統計資訊:

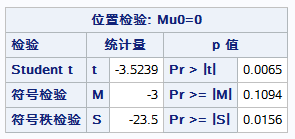
下圖顯示秩檢驗的p值<0.05的顯著水平,應拒絕原假設:
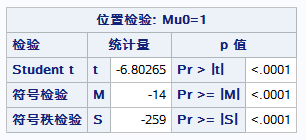
兩樣本的非引數檢驗
概述: 當兩個獨立樣本來自正態分佈和具有相同的方差時,一般採用T檢驗比較均值。當樣本不滿足這兩個條件時,則採用Wilcoxon秩和檢驗。
對某校高一高二學生的英語學習能力作評價,主要測試學生的口語能力,測試分數如下,分析兩個年級的學生英語口語能力是否有顯著差異?
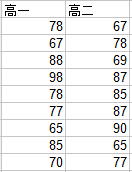
程式碼:
data test; /*建立資料集*/ input x type$; cards; 78 1 67 1 88 1 98 1 78 1 77 1 65 1 85 1 70 1 67 2 78 2 69 2 87 2 85 2 87 2 90 2 65 2 77 2 ; run; proc npar1way data=test wilcoxon; /*進行wilcoxon檢驗*/ class type; /*指定分組變數*/ var x; /*指定非引數檢驗變數*/ run;
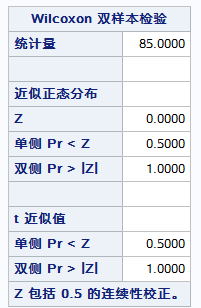
結果:
t檢驗雙邊概率值為1,故可接受原假設,認為這兩個年級的口語能力是無顯著差別的。
多個樣本的非引數檢驗
概述: 當多個樣本資料滿足正態分佈且具有相等的方差時,比較它們的均值可以採用方差分析。當資料不滿足上述條件時,可採用多樣本均值比較的非引數Kruskal-Wallis秩和檢驗。此檢驗的目的是分析某個變數在另一分類變數取不同值時,它的取值(用位置統計量衡量)是否有顯著不同。
程式設計實現: NPAR1WAY過程可以實現,與兩樣本情形不同的是,class語句的分類變數它有兩個以上的取值水平。
成對樣本的非引數檢驗
類似於單樣本的非引數檢驗,使用Univariate過程,成對的資料作差處理,檢驗其均值是否顯著為0。
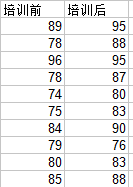
現對某培訓機構的培訓後的學員的基礎能力是否有提高進行抽樣調查,學生培訓前後的成績如下表。
程式碼:
data test; /*建立資料集*/
input x y;
d=x-y;
cards;
89 95
78 88
96 95
78 87
74 80
75 83
84 90
79 76
80 83
85 88
;
run;
proc univariate data=test; /*配對樣本的符號檢驗*/
var d;
run;
結果:
符號檢驗的p值大於0.05,說明應該接受原假設,即認為培訓前後的成績沒有顯著差別。