皮爾森擬合優度卡方檢驗

該檢驗的主要目的是：
由樣本評估群體是否符合某種分佈情況。

假設H0：群體具有某分佈
備選假設H1：群體不具有改分佈
思路：將數軸分為m組，樣本資料會落入不同的組內。根據假設H0的分佈，我們可以確定各個組的預期個數，然後與各個組的實際個數一起構造統計量K。
結論：當n趨於無窮時，k收斂於m-1的卡方分佈。

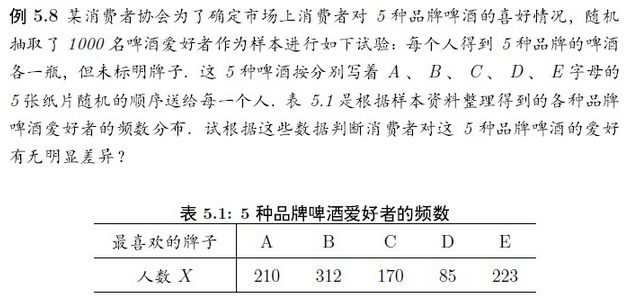
#如果是均勻分佈，則沒有明顯差異 。這裡組其實已經分好了，直接用 。
#H0：人數服從均勻分佈
x <- c(210,312,170,85,223)
n <- sum(x); m <- length(x)
p <- rep(1
 
/m,m)
K <- sum((x-n*p)^2/(n*p)); K #計算出K值
[1] 136.49
p <- 1-pchisq(K,m-1); p #計算出p值,0拒絕假設

在R語言中 chisq.test()，可以完成擬合優度檢驗。預設就是檢驗是否為均勻分佈，如果是其他分佈，需要自己分組，並在引數p中指出。上面題目的解法

chisq.test(x)

其他例子如下：

#例：用這個函式檢驗其他分佈。 抽取31名學生的成績，檢驗是否為正態分佈。
#小於0.05,拒絕正態分佈的假說
x <- c(25,45,50,54,55,61,64,68,72,75,75,78,79
 
,81,83,84,84,84,85,
       86,86,86,87,89,89,89,90,91,91,92,100)
A = table(cut(x,breaks=c(0,69,79,89,100))) #對樣本資料進行分組
A
p = pnorm(c(70,80,90,100),mean(x),sd(x)) #獲得理論分佈概率值
p = c(p[1],p[2]-p[1],p[3]-p[2],1-p[3])
p
chisq.test(A,p=p)

#例：大麥雜交後關於芒性的比例應該是 無芒：長芒：短芒=9:3:4 。 
#我們的實際觀測值是335：125：160 。請問觀測值是否符合預期？
p <- c(9
 
/16,3/16,4/16)
x <- c(335,125,160)
chisq.test(x,p=p)

注意：
1. 分組的時候每組的頻數應該大於5。
2. 如果理論分佈依賴於多個未知引數，則先用樣本得到引數的估計值，然後構造統計量K。這個時候K的自由度減少未知引數的數量個數。

ks檢驗

該檢驗的目的是：
1. 對於單樣本，檢驗其是否符合某種分佈
2. 對於雙樣本，檢驗其是否屬於同一分佈

ks檢驗，理論上可以檢驗任何分佈。
ks檢驗，既可以做當樣本檢驗，也可以做雙樣本檢驗。

#單樣本檢驗
#記錄一臺裝置無故障工作時常，並從小到大排序
#420 500 920 1380 1510 1650 1760 2100 2300 2350。
#問這些時間是否服從lambda=1/1500的指數分佈？
x <- c(420,500,920,1380,1510,1650,1760,2100,2300,2350)
ks.test(x,"pexp",1/1500)

#雙樣本檢驗
#有兩個分佈，分別抽樣了一些資料，問他們是否服從相同的分佈。
X<-scan()
Y<-scan()
x = runif(100)
y = runif(100)
ks.test(x,y)

列聯表資料獨立性檢驗

chisq.test() 同樣可以做列聯表資料獨立性檢驗，只要將資料寫成矩陣的形式就可以了。

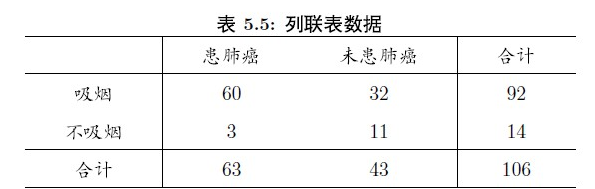
#根據列聯表判斷吸菸與致癌是否有關係
#p值很小，拒絕無關係的假設，應該有關係
x = matrix(c(60,3,32,11),nrow=2)
chisq.test(x)

#如果一個單元格內的資料小於5，那麼pearson檢驗無效。
#此時應做Fisher精確檢驗
fisher.test(x)

此外，還有針對配對資料的McNemar檢驗

符號檢驗

當我們以中位數將資料分為兩邊，一邊為正，一邊為負，那麼樣本出現在兩邊的概率應該都為1/2。因此，使用p=0.5的二項檢驗就可以做符號檢驗了。

#統計了66個城市的生活花費指數，北京的生活花費指數為99 。
#請問北京是否位於中位數以上。
x = c(66, 75, 78, 80, 81, 81, 82, 83, 83, 83, 83,
      84, 85, 85, 86, 86, 86, 86, 87, 87, 88 ,88,
      88, 88 ,88 ,89 ,89 ,89 ,89 ,90 ,90 ,91, 91,
      91, 91, 92, 93, 93, 96, 96, 96, 97, 99, 100,
      101 ,102, 103, 103, 104, 104, 104, 105, 106, 109, 109,
      110 ,110 ,110 ,111 ,113 ,115 ,116 ,117, 118, 155 ,192)
mean(x)
binom.test(sum(x>99),length(x),p=0.5,alternative = "less")

符號檢驗也可以用來檢驗兩個總體是否存在明顯差異。要是沒有差異，那麼兩者之差為正的概率為0.5。

#統計兩種飼料養豬的增重情況，判斷是否有差異
#其實用均值更好
#沒有明顯差異
y <- c(19,32,21,19,25,31,31,26,30,25,28,31,25,25)
x <- c(25,30,28,23,27,35,30,28,32,29,30,30,31,16)
binom.test(sum(x<y),length(x),p=0.5,alternative = "two.sided")  #並不推薦這麼檢驗

var.test(x,y) #方差相等
t.test(x,y,var.equal = T) #沒有顯著差異

#p<0.1 接受備擇假設 認為有差異
binom.test(3,12,alternative = "less",conf.level = 0.9)

秩相關檢驗

在R語言中，rank()函式用來求秩，如果向量中有相同的資料，求出的秩可能不合我們的要求，對資料做微調即可

x <- c(1.2,0.8,-3.1,2,1.2)
rank(x)
x <- c(1.2,0.8,-3.1,2,1.2+1e-5)
rank(x)

利用秩可以做相關性檢驗。具體參考引數估計。
cor.test( method=”spearman,kendell”)

wilcoxon檢驗

符號檢驗只考慮了符號，沒有考慮要差異的大小。wilcoxon解決了這個問題。
假設，資料是連續分佈的，資料是關於中位數對稱的。

#單樣本檢測
#某電池廠商生產的電池中位數為140.
#現從新生產的電池中抽取20個測試。請問電池是否合格
x <- c(137,140,138.3,139,144.3,139.1,141.7,137.3,133.5,
       138.2,141.1,139.2,136.5,136.5,135.6,
       138,140.9,140.6,136.3,134.1)
wilcox.test(x,mu=140,alternative = "less",
            exact=F,correct=F,confi.int=T)
#配對雙樣本檢測。
#在農場中選擇了10塊農田，將每一塊農田分成2小塊，分別用不同的化肥種菜。
#請問化肥會不會提高蔬菜產量。
x <- c(459,367,303,392,310,342,421,446,430,412)
y <- c(414,306,321,443,281,301,353,391,405,390)
wilcox.test(x-y,alternative = "greater")
#非配對雙樣本檢測
#10名非鉛工人和10名鉛工人的血鉛值是否存在顯著差異
x <- c(24,26,29,34,43,58,63,72,87,101)
y <- c(82,87,97,121,164,208,213)
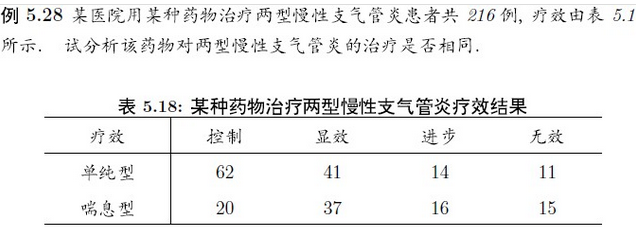
wilcox.test(x,y,alternative="less")

x <- rep(1:4,c(62,41,14,11))
y <- rep(1:4,c(20,37,16,15))
wilcox.test(x,y)

參考資料

非引數檢驗