數論練習1題解B

新號，新開始。第一篇題解。

先上題目(HDU1395）

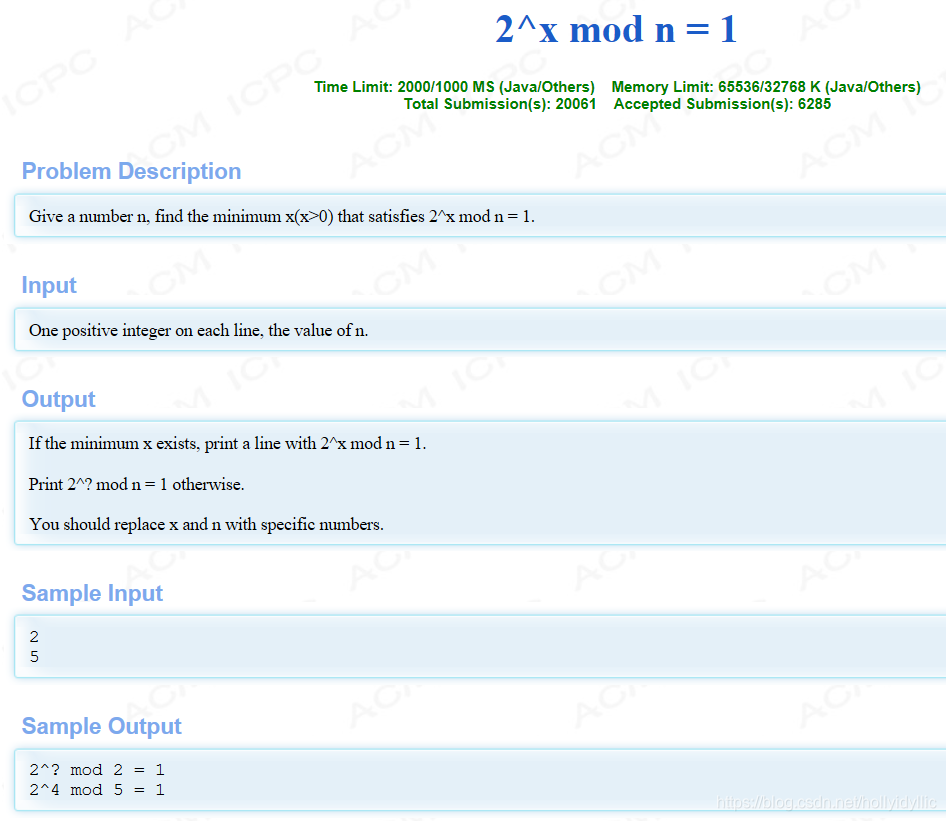
這道題目上來就沒有資料範圍（捂住額頭真的合適嘛）
然後就是一句話 暴力能過（那你給個數據範圍能怎麼樣嘛）
暴力的思路也就是運用同餘性質用迴圈不斷嘗試2^i直到滿足條件，每次乘2求餘，直到餘數為1

**#include<iostream>
using namespace std;
int main()
{
 long long i,t,n;
 while(cin>>n)
 {
 t=1;
 if (n==1||n%2==0) cout<<0<<endl;
 else
 { 
 t=t*2;
 for (i=2;i<=n-1;i++)
 if (t!=1) t=(t*2)%n; else break;
 cout<<i-1<<endl;
 }
}
 return 0;
}
 

但暴力過明顯**不優雅（因為平常練習 總要多思考一下）
由數論我們可以知道幾個結論（證明此處略）
1：我們用φ(n)表示滿足條件的最小2^k
2：對於n=(p1^k1)
(p2^k2)…
(pn^kn)
我們有φ（n)=[φ(p1^k1),…]（即最小公倍數）（此易證）
3：對於φ(p1^k1) 我們可以由數學歸納法得到
它等於φ（p1)*p1^(k1-1)
然後就可以簡化一些 但是對於大素數 當時並沒有發現好的處理方法
然後貼程式碼 如下

#include<iostream>
#include<cstring> 
#include<cmath>
using namespace std;
int pd[100001];
int gcd(int,int);
int main()
{
 int i,j,t,tn,num,n;
 memset(pd,0,sizeof(pd));
 pd[1]=1;
 for (i=2;i<=50000;i++)
 {
  if (pd[i]==0) 
  {
   tn=2;
   for (j=1;j<i;j++)
   if (tn==1) break;else tn=(tn*2)%i;
   pd[i]=j;
  for (j=2;j<=50000/i;j++)
  pd[i*j]=1;
  }
 }
 while (cin>>n)
 {
  if (n%2==0||n==1) cout<<"2^? mod "<<n<<" = 1"<<endl;
  else
  {
  if (pd[n]!=1) cout<<"2^"<<pd[n]<<" mod "<<n<<" = 1"<<endl;
   else
   { 
       t=0;
    for (i=3;i<=n/2;i++)
     if (pd[i]!=1&&n%i==0) 
     {
      tn=n;
      num=0;
      while (tn%i==0)
      {
      num++;
      tn=tn/i;
      }
      tn=pd[i];
      for (j=2;j<=num;j++) 
       tn=tn*i;
      t=gcd(t,tn);
     }
    cout<<"2^"<<t<<" mod "<<n<<" = 1"<<endl;
   }
 }
}
 return 0;
}
int gcd(int a,int b)
{
 if (a==0) return b;
 else
 {
  int temp,ta,tb;
  ta=a;
  tb=b;
  if (a<b) 
  {
   temp=a;
   a=b;
   b=temp;
  }
  while (b!=0)
  {
   temp=a%b;
   a=b;
   b=temp;
  }
  return ta*tb/a;
 }
}
 

就這樣了 好久不寫了 也不知說啥 新的第一篇就這樣吧。