數論練習1題解A
阿新 • • 發佈:2018-12-02
數論練習1題解A
先貼題

此題有兩個思路
法1:運用費馬定理和同餘 則結果同餘與2^k,(k為對n求1e9+6的模)
此處可一位位讀求 也可 高精度
備註:以上均要使用快速冪
程式碼如下
#include<iostream> #include<cstring> using namespace std; char ch[100002]; long long power(int,long long ); int main() { long long s; int i; memset(ch,0,sizeof(ch)); while(cin>>ch) { s=0; i=0; while (ch[i]!='\0') { s=(s*10+ch[i]-48)%1000000006; i++; } memset(ch,0,sizeof(ch)); cout<<power(2,s-1)<<endl; } } long long power(int a,long long b) { long long r=1,base=a; while(b!=0) { if(b%2) r=(r*base)%1000000007; base=(base*base)%1000000007; b/=2; } return r; }
法2:
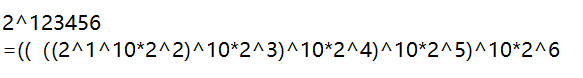
每次此方和和乘法都要求餘
備註:以上均要使用快速冪
下面貼程式碼
#include<iostream> #include<cstring> using namespace std; char ch[100002]; long long power(long long ,int ); int main() { long long s; int i; memset(ch,0,sizeof(ch)); while(cin>>ch) { s=0; i=0; while (ch[i]!='\0') { s=(power(s,10)*power(2,ch[i]-48))%1000000007; i++; } memset(ch,0,sizeof(ch)); if (s%2!=0) s=s+1000000007; cout<<s/2<<endl; } } long long power(long long a,int b) { long long r=1,base=a; if (a==0) return 1; else { while(b!=0) { if(b%2) r=(r*base)%1000000007; base=(base*base)%1000000007; b/=2; } return r; } }
以上
