卷積神經網路架構
卷積神經網路(conv)架構
卷積神經網路在影象分類資料集上有非常突出的表現,由於一般正常的影象資訊過大,如果使用全連線神經網路,需要設定大量的權值w和basic值,這樣會導致運算效率較低,還容易導致過分擬合的問題。
1.全連線神經網路和卷積神經網路的區別
全連線神經網路:
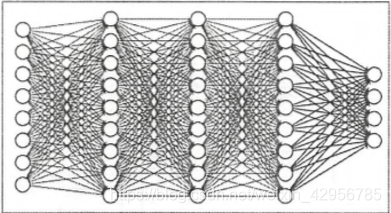
卷積神經網路圖:
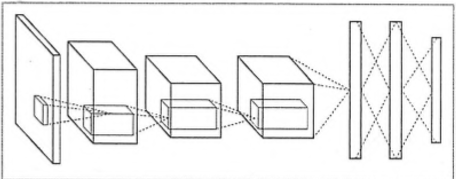
共同點: 圖中每一個節點都代表一個神經元,沒相鄰兩層之間的節點都有邊相;輸入輸出的流程基本一致。
不同點: 卷積神經網路相鄰兩層之間只有部分的節點相連,所以一般會將每一層的卷積層組織成一個三維矩陣。
卷積神經網路的優點: 在影象處理方面,對於MNIST資料,每一張圖片的大小是2828
2.卷積神經網路
卷積神經網路構架圖:
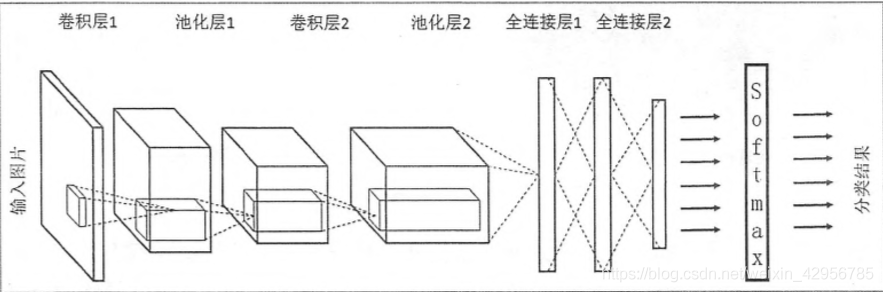
1.輸入層
在處理影象的卷積神經網路中,它一般代表了一張圖片的畫素矩陣。通常為(length * width *channel)。 三維矩陣的深度代表了影象的彩色通道(channel)
2.卷積層
是卷積網路中最為重要的部分。和傳統全連線層不同,卷積層中每一個節點的輸入只是上一層神經網路的一小塊,這個小快常用的大小有3 * 3或者5 * 5,卷積層會增加原始節點的深度。通常卷積層這部分被稱為過濾器(filetr) 或者 核心(kernel)。
過濾器: 將當前的神經網路上的一個子節點矩陣轉化為下一層神經網路上的一個單位節點矩陣,但深度不限的節點矩陣。
過濾器示意圖:
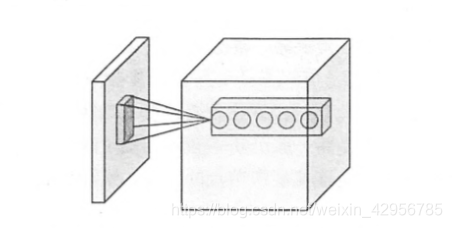
過濾器的尺寸: 過濾器的所處理的節點矩陣的長和寬就是這個過濾器的長和寬的尺寸。而過濾器的深度則是有需要人工指定設定和處理的。
卷積層例子:
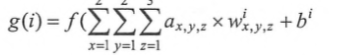
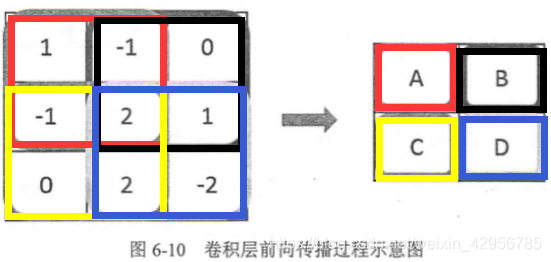
傳播的過程: 卷積層的前向傳播過程是將一個過濾器從神經網路當前層的 左上角移動到右下角,並且在移動過程中計算每一個對應的單位矩陣。移動的例圖 (步長為1):
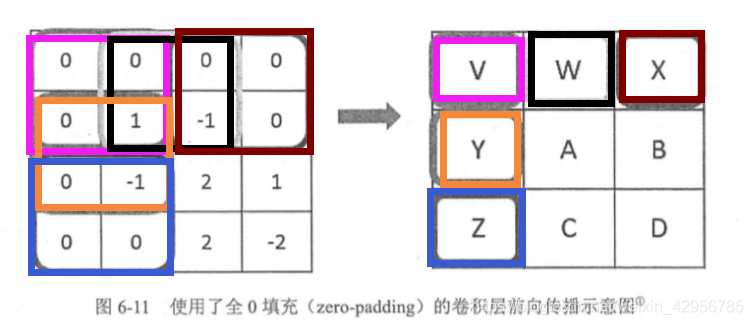
全0填充(zero-padding)–改變結果矩陣的大小(1): 為了 避免尺寸的變化,可以在當前層矩陣的邊界加入全0填充。這樣可以使得卷積層前向傳播結果的矩陣大小和當前層矩陣保持一致。示意圖:
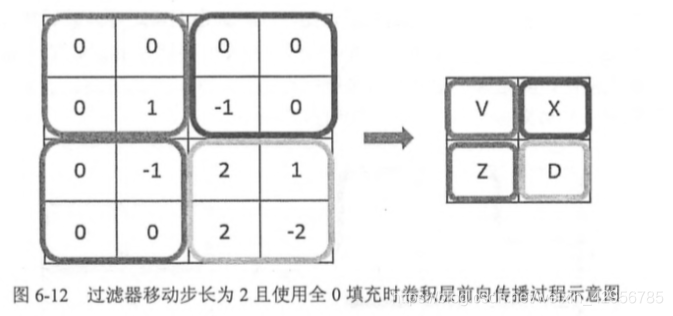
**改變移動步長–改變結果矩陣的大小(2):**當改變過濾器的移動步長,可以改變結果矩陣的尺寸大小,示意圖:
計算結果矩陣的大小的尺寸:
1.使用全0填充時:
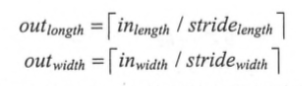
2.不使用全0填充:

in_length:輸入節點的長度,in_width:輸入節點的寬度,side_length:移動的步長,filter_length過濾器的長度,filter_width表示過濾器的寬度。
3.池化層(Pooling)
池化層神經網路不會改變三維矩陣的深度,但是它可以縮小矩陣的大小。池化操作可以認為是將一張解析度較高的圖片轉化為解析度較低的圖片。通過池化層,可以進一步縮小最後全連線層中節點的個數,從而達到減少整個神經網路中的引數的目的。
效果: 使用池化層既可以加快計算速度也可以防止過度擬合。
使用: 同樣類似卷積層,但是並不是計算節點的加權和,而是採用更加簡單的最大值或者平均值運算。 最大池化層(max pooling) 使用最大值操作,是被使用得最多的池化層結構。平均池化層(average pooling) 使用平均值操作。注意: 池化層不僅需要在長和寬的維度上移動,它還需要在深度的維度上移動,且每次的過濾器可能是 不同的 。如圖:
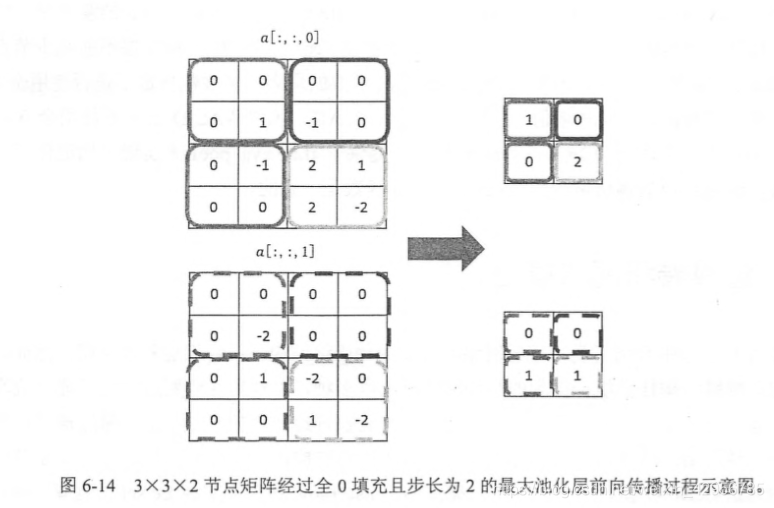
4.全連線層
在經過幾輪的卷積層和池化層的處理之後,可以認為影象中的資訊已經被抽象成了資訊含量更高的特徵。我們可以將卷積層和池化層看成自動影象特徵提出的過程。在此之後,我們仍需使用全連線層來完成分類任務。
5.Softmax層。
Softmax層主要用於分類問題,我們可以得到當前樣例屬於不同種類的概率分佈情況。
以上所有內容均為小編在看書後做的一些筆記總結。
