1. 神經元模型

神經網路是由具有適應性的簡單單元組成的廣泛並行互連的網路，它的組織能夠模擬生物神經系統對真實世界物體所作出的互動反應。
神經網路中最基本的成分是神經元 (neuron)模型，即上述定義中的"簡單單元"在生物神經網路中，每個神經元與其他神經元相連，當它"興奮"時，就會向相連的神經元傳送化學物質，從而改變這些神經元 內的電位;如果某神經元的電位超過了 一個"闊值" (threshold) ， 那麼它就會被啟用，即 "興奮 "起來，向其他神經元傳送化學物質。
1943 年， [McCulloch and Pitts, 1943] 將上述情形抽象為圖所示的簡單模型，這就是一直沿用至今的 "M-P 神經元模型 " 在這個模型中，神經元接收到來自n個其他神經元傳遞過來的輸入訊號$\{ {x_1},{x_2},...,{x_i},...,{x_n}\} $，這些輸入訊號通過帶權重$\omega$的連線( connection)進行傳遞，神經元接收到的總輸入值$\sum\nolimits_i {{\omega _i}{x_i}}$將與神經元的閥值進行比較，然後通過"啟用函式" (activation function)$f()$處理以產生神經元的輸出。

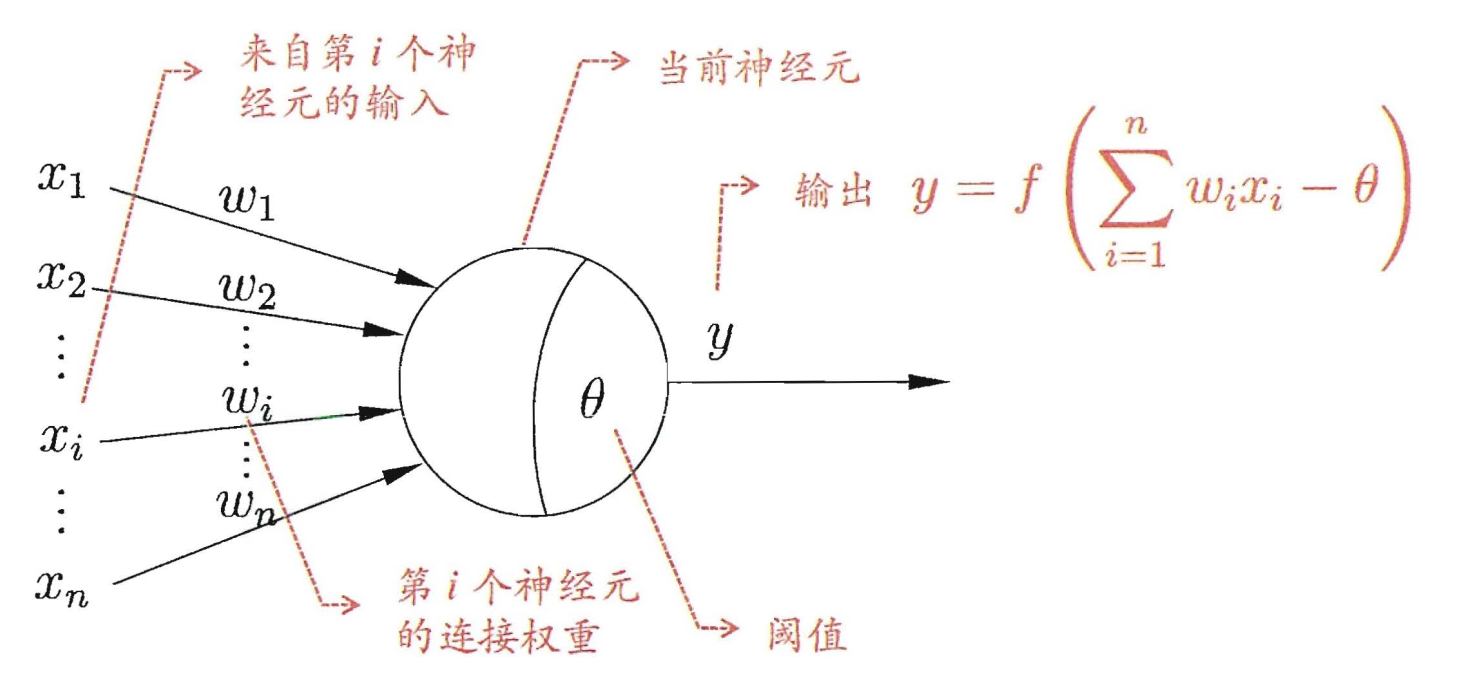
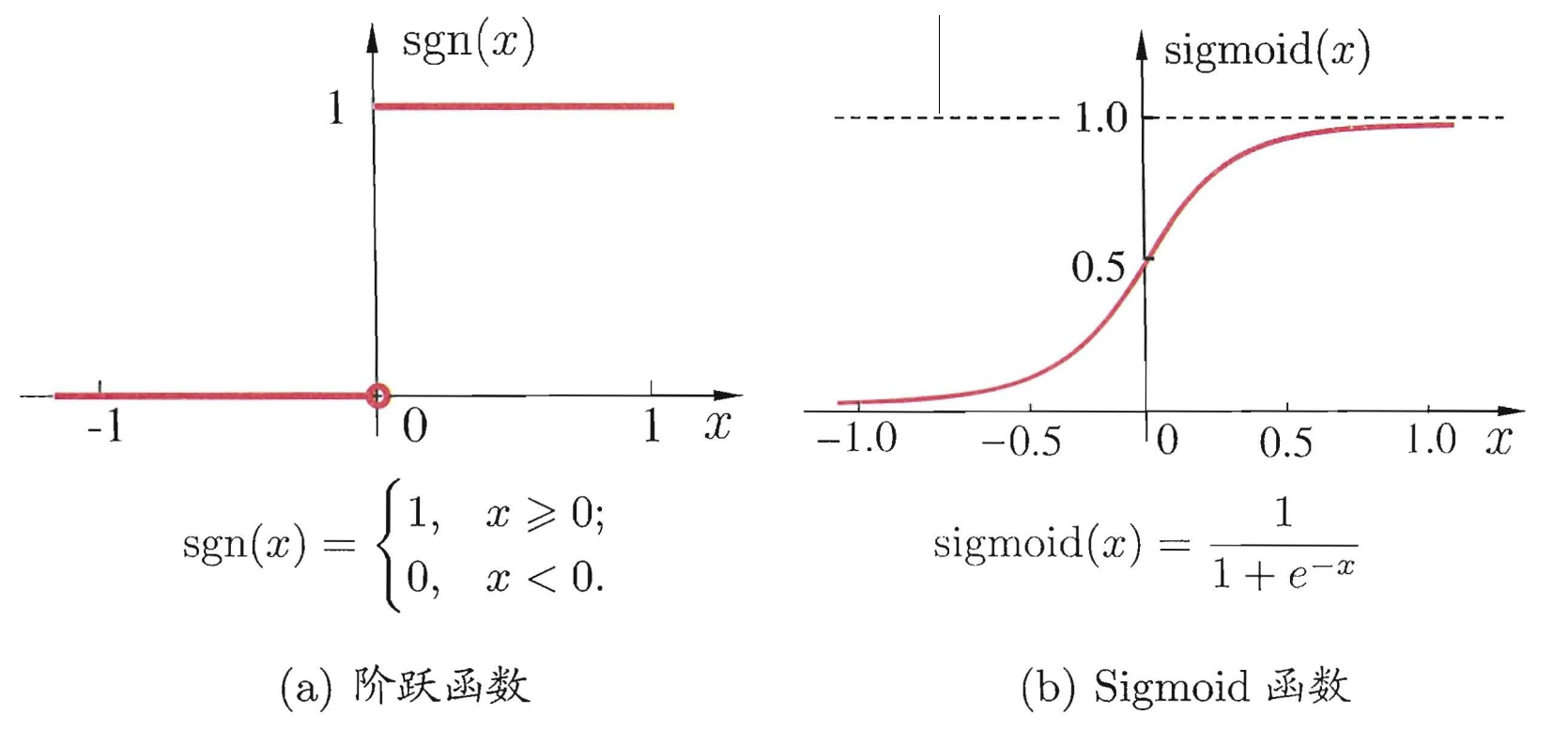
理想啟用函式$f()$理想中的啟用函式是下圖左邊所示的階躍函式，它將輸入值對映為輸出值 "0" 或"1"，顯然 "1" 對應於神經元興奮，"0" 對應於神經元抑制。然而，階躍函式具有不連續 、不光滑等不太好的性質，因此實際常用 Sigmoid函式作為啟用。函式典型的 Sigmoid函式如下圖右邊所示，它把可能在較大範圍內變化的輸入值擠壓到 (0， 1) 輸出值範圍內，因此有時也稱為 "擠壓函式" (squashiing function).

事實上，從電腦科學的角度看，我們可以先不考慮神經網路是否真的模擬了生物神經網路，只需將一個神經網路視為包含了許多引數的數學模型，這個模型是若干個函式，例如${y_j} = f\left( {\sum\nolimits_i {{\omega _i}{x_i}} - {\theta _j}} \right)$相互(巢狀)代入而得。有效的神經網路學習演算法大多以數學證明為支撐 。

2. 感知機與多層網路

感知機(Perceptron) 由兩層神經元組成，如圖所示，輸入層接收外界輸入訊號後傳遞給輸出層， 輸出層是 M-P 神經元，亦稱"閾值邏輯單元" (threshold logic unit)。

更一般地，給定訓練資料集，權重${\omega _i}(i = 1,2,...,n)$以及閾值$\theta$。可通過學習得到。閾值可看作一個固定輸入為-1. 0的"啞結點" (dummy node) 所對應的連線權重${\omega _{n+1}}$，這樣，權重和閾值的學習就可統一為權重的學習。

在學習的過程中，如果感知機對訓練樣例的預測是對的，那麼權重不更新，感知機不發生變化；若果預測錯誤，則按照一定的學習率更新權重，調整感知機。

若兩類模式是線性可分的，即存在一個線性超平面能將它們分開，則感知機的學習過程一定會收斂 (converge) 而求得適當的權向量${\bf{\omega }} = ({\omega _1};{\omega _2};...;{\omega _{n + 1}})$；否則感知機學習過程將會發生振盪(fluctuation) ， ${\bf{\omega }}$難以穩定下來，不能求得合適解。

要解決非線性可分問題，需考慮使用多層功能神經元。輸出層與輸入居之間的一層神經元，被稱為隱居或隱含層 (hidden layer)，隱含層和輸出層神經元都是擁有啟用函式的功能神經元。

更一般的，常見的神經網絡是形如下圖所示的層級結構，每層神經元與下層神經元全互連，神經元之間不存在同層連線， 也不存在跨層連線。這樣的神經網路結構通常稱為" 多層前饋神經網絡 " (multi-layer feedforward neural networks) ，其中輸入層神經元接收外界輸入，隱層與輸出層神經元對信弓進行加工，最終結果由輸出層神經λ輸出；換言之，輸入層神經元僅是接受輸入，不進行函式處理，隱居與輸出層包含功能神經元。因此，通常被稱為"兩層網路"。為避免歧義，本書稱其為"單隱層網路"。只需包含隱層，即可稱為多層網路。神經網路的學習過程，就是根據訓練資料來調整神經元之間的"連線權" (connection weight) 以及每個功能神經元的闌值；換言之，神經網路"學"到的東西，蘊涵在連線權與闕值中。

3. 誤差逆傳播演算法

多層網路的學習能力比單層感知機強得多。欲訓練多層網路，需要更強大的學習演算法來更新權值，誤差逆傳播 (error BackPropagation，簡稱 BP)演算法就是其中最傑出的代表。它是迄今最成功的神經網路學習演算法。現實任務中使用神經網路時，大多是在使用 BP 演算法進行訓練。值得指出的是，BP 演算法不僅可用於多層前饋神經網路，還可用於其他型別的神經網路。但通常說 "BP 網路"時，一般是指用 BP 演算法訓練的多層前饋神經網路。

給定訓練集需要擬合的資料集是$D = \left\{ {({X_1},{y_1}),({X_2},{y_2})...,({X_n},{y_n})} \right\},{X_n} \in {R^d},{y_n} \in {R^l}$，即輸入示例由$d$個屬性描述，輸出$l$實值向量。

以下圖網路為例，其中神經元都使用sigmoid函式，

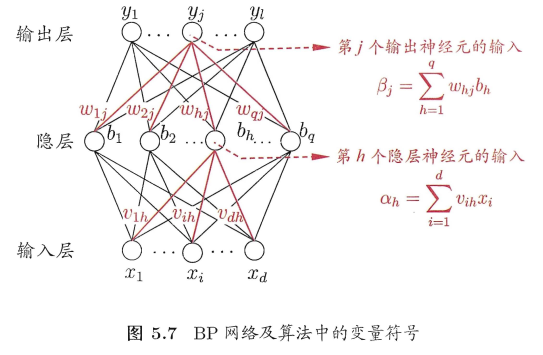
對與訓練集D中的某一個訓練樣本$({X_k},{y_k})$，假定神經網路的輸出為，$\hat{y_k} = (\hat{y_k^1},\hat{y_k^2},...\hat{y_k^l})$.

則神經網路在$({X_k},{y_k})$的均方誤差為，

\[E_k = \frac{1}{2}\sum\limits_{j = 1}^l {{{(\hat{y_k^j} - y_k^j)}^2}} \]

BP演算法基於梯度下降策略，以目標的負梯度方向對每個引數進行逐步調整，任意引數v的更新估計式為，

\[v \leftarrow v - \alpha \Delta v\]

對隱層到輸出層的連線權來說，$\omega _{h,j}$先影響到第 j 個輸出層神經元的輸入值$\beta _j$，再影響到其輸出值$\hat{y_k^j}$，最後影響到$E_k$，

\[\Delta {\omega _{h,j}} =   \frac{{\partial {E_k}}}{{\partial {\omega _{h,j}}}} =   \frac{{\partial {E_k}}}{{\partial \hat{y_k^j}}}\frac{{\partial \hat{y_k^j}}}{{\partial {\beta _j}}}\frac{{\partial {\beta _j}}}{{\partial {\omega _{h,j}}}}\]

 其中，

\[\begin{array}{l}
\frac{{\partial {\beta _j}}}{{\partial {\omega _{h,j}}}} = {b_h}\\
\frac{{\partial \hat{y_k^j}}}{{\partial {\beta _j}}} = f'({\beta _j} - {\theta _j})\\
\frac{{\partial {E_k}}}{{\partial \hat{y_k^j}}} = \hat {y_k^j} - y_k^j
\end{array}\]

sigmoid函式f(x)有一個很好的性質$f'(x) = f(x)(1 - f(x))$，所以，

\[\frac{{\partial {E_k}}}{{\partial \hat{y_k^j}}}\frac{{\partial \hat{y_k^j}}}{{\partial {\beta _j}}}\frac{{\partial {\beta _j}}}{{\partial {\omega _{h,j}}}} = (\hat {y_k^j} - y_k^j)\hat {y_k^j}(1 - \hat {y_k^j}){b_h}\]

類似可求得其他引數的更新梯度。

學習率$\alpha  \in (0,1)$控制著算沾每一輪迭代中的更新步長，太大則容易振盪，太小則收斂速度又會過慢。有時為了做精細調節，可令各引數的學習率不一樣。

輸入：訓練集$D = \left\{ {({X_k},{y_k})} \right\}_{k = 1}^m,{X_k} \in {R^d},{y_k} \in {R^l}$

　　　學習率$\alpha$

過程：初始化網路中的所有連線權和閾值

repeat

for all $({X_k},{y_k}) \in D$ do

根據當前網路引數計算當前樣本的輸出$\hat{y_k}$

根據公式更新各個引數

end for

until 達到終止條件

輸出：連線權和閾值確定的多層前饋神經網路

需注意的是， BP 演算法的目標是要最小化訓練集 D 上的累積誤差

\[E = \frac{1}{m}\sum\limits_{m = 1}^k {{E_k}} \]

但我們上面介紹的"標準 BP 演算法"每次僅針對一個訓練樣例更新連線權和閾值， 也就是說，標準BP演算法的更新規則是基於單個的$E_k$推導而得。果類似地推匯出基於累積誤差最小化的更新規則，就得到了累積誤差逆傳播 (accumulated error backpropagation)演算法累積 BP 演算法與標準 BP 演算法都很常用.一般來說，標準 BP 演算法每次更新只針對單個樣例，引數更新得非常頻繁，而且對不同樣例進行更新的效果可能出現"抵消"現象.因此，為了達到同樣的累積誤差極小點，標準 BP 演算法往往需進行更多次數的法代.累積 BP 演算法直接針對累積誤差最小化，它在讀取整個訓練集D一遍後才對引數進行更新，其引數更新的頻率低得多。但在很多工中，累積誤差下降到一定程度之後，進一步下降會非常緩慢，這時標準 BP 往往會更快獲得較好的解，尤其是在訓練集 D 非常大時更明顯。

[Hornik et al., 1989] 證明，只需二個包含足夠多神經元的隱層，多層前饋網路就能以任意精度逼近任意複雜度的連續函式。然而，如何設定隱層神經元的個數仍是個未決問題，實際應用中通常靠"試錯法" (trial-by-error)調整.

正是由於其強大的表示能力， BP 神經網路經常遭遇過擬合，其訓練誤差持續降低，但測試誤差卻可能上升有兩種策略常用來緩解BP網路的過擬合。第一種策略是"早停" (early stopping)：將資料分成訓練集和驗證集，訓練、集用來計算梯度、更新連線權和闊值，驗證集用來估計誤差，若訓練集誤差降低但驗證集誤差升高，則停止訓練，同時返回具有最小驗證集誤差的連線權和闌值。 第二種策略是"正則化" (regularization) ，其基本思想是在誤差目標函式中增加一個用於描述網路複雜度的部分，例如連線權與閾值的平方和。修改誤差目標函式為，

\[E = \lambda \frac{1}{m}\sum\limits_{m = 1}^k {{E_k}}  + (1 - \lambda )\sum\nolimits_i {\omega _i^2} \]

其中$\lambda  \in (0,1)$用於對經驗誤差與網路複雜度這兩項進行折中，常通過交叉驗證法來估計。 

參考：

機器學習 周志華