本文是摘抄學習大神 計算機的潛意識   文章 https://www.cnblogs.com/subconscious/p/5058741.html

神經網路是一種模擬人腦的神經網路，期望能夠實現類人的人工智慧機器學習技術。

一、經典神經網路模型

這個模型包含三個層次的神經網路，紅色是輸入層(3個輸入單元)，綠色是輸出層(2個單元)，紫色是隱藏層（4個單元）

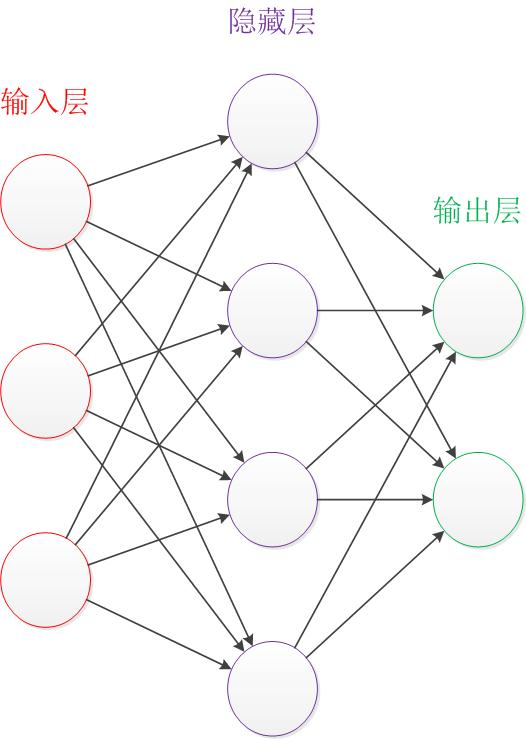
神經網路模型知識點：

• 輸入層和輸出層的節點數一般是固定的，隱藏層可以自由設定
• 神經網路結構圖的拓撲與箭頭代表預測過程資料的流向，和訓練的資料流有一定的區別
• 結構圖的關鍵不是神經元(圖中圓圈)，而是連線線(圖中圓圈的連線線)，每個連線線對應一個不同的權重(值稱為權值)，權重是訓練得到

二、神經元模型

 神經元包含輸入、輸出和計算功能的模型，下圖包含3個輸入、1個輸出、以及二個計算功能的模型

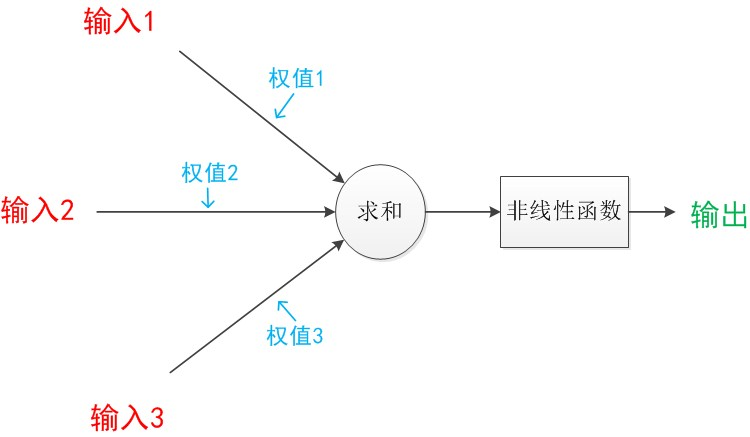
連線是神經元中最重要的東西，每個連線上都有一個權重。

神經網路演算法就是讓權重值調整到最佳，以到達模型預測的效果最好。

使用a表示輸入特徵變數，w來表示權重值，一個連線的有向箭頭表示：a經過連線加權變成了aw

對於多特徵變數的神經元模型，如下圖，其中：z = g(a₁w₁+a₂w₂+a₃w₃)為輸出計算公式

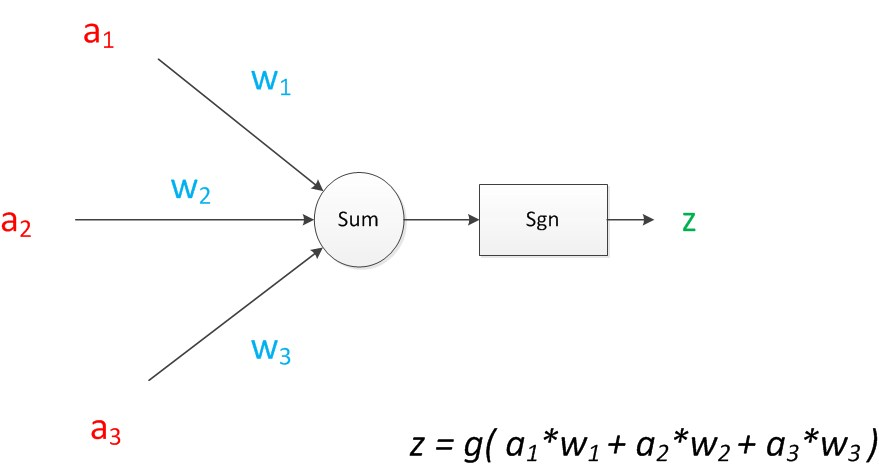
在MP模型裡，函式g是sgn函式：當輸入大於0時輸出為1，小於0是輸出為0

把sum函式和sgn函式合併，神經元可以看作一個計算和儲存單元，計算是神經元對輸入進行計算，儲存是神經元會暫存計算結果，並傳遞到下一層。

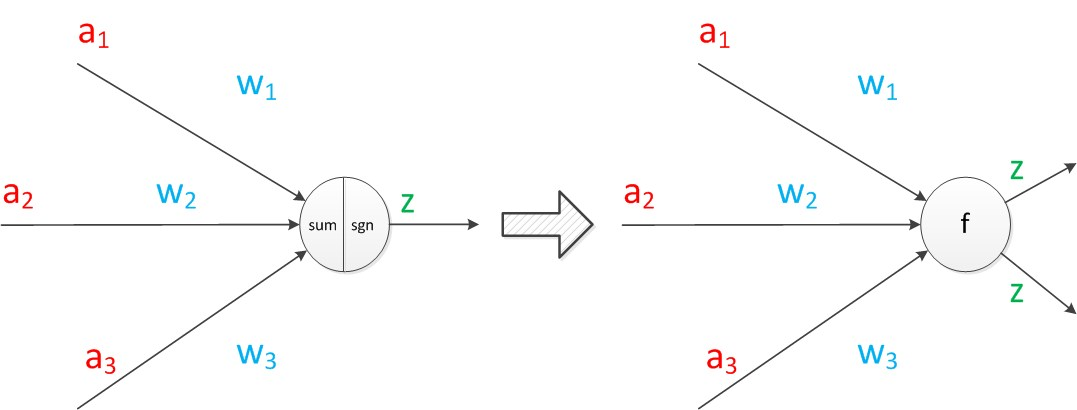
整個模型就是對函式：z = g(a₁w₁+a₂w₂+a₃w₃)結果的預測，通過已知的樣本a_1,a_2,a₃特徵和對應的標籤z₁,z₂,z₃，得出最優的w_1,w_2,w₃權重，最後預測出z標籤值

三、單層神經網路

在MP模型的輸入位置新增神經元節點，標誌其為輸入單元(負責傳輸資料，不計算)，輸出層的輸出單元需要對前一層對輸入進行計算。

有兩個輸出單元的模型，用w_x,y來表達一個權值。下標中的x代表後一層神經元的序號，而y代表前一層神經元的序號（序號的順序從上到下）。

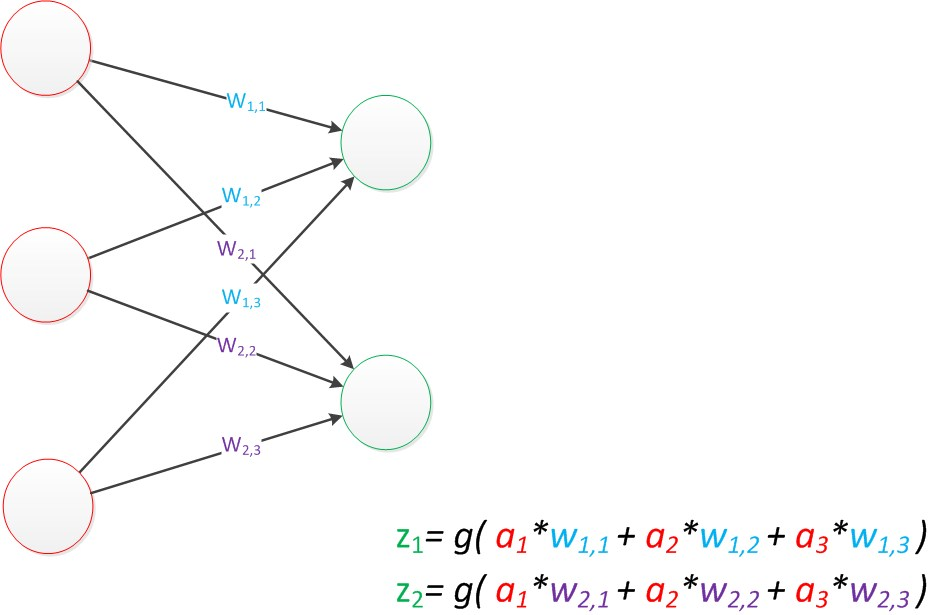
分析圖上兩個公式，可以向量化：

輸入特徵變數：a = [a₁ a₂ a₃]^T(T代表轉置矩陣)，預測值：z = [z₁

輸出公式向量化表示： z = g(Wa)   (神經網路前一層計算後一層的矩陣運算)

神經網路類似一個logistic迴歸，可以做分類任務。決策界限表示分類效果

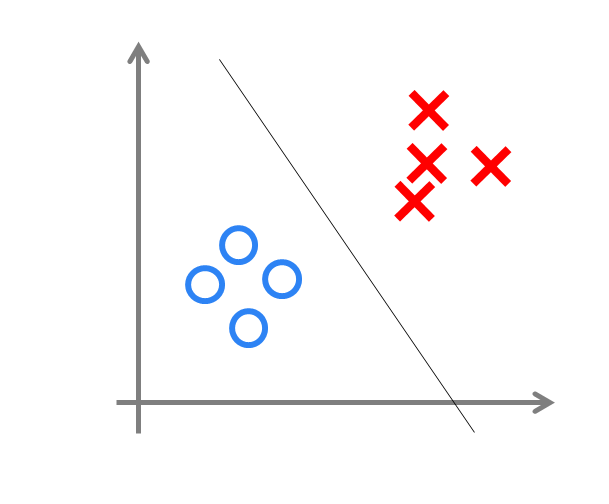
四、兩層神經網路模型

兩層神經網路包含一個輸入層、一個輸出層和一個隱藏層，隱藏和輸出層都是計算層。

a_x^(y)代表第y層的第x個節點。z₁，z₂變成了a₁⁽²⁾，a₂⁽²⁾。下圖給出了a₁⁽²⁾，a₂⁽²⁾的計算公式

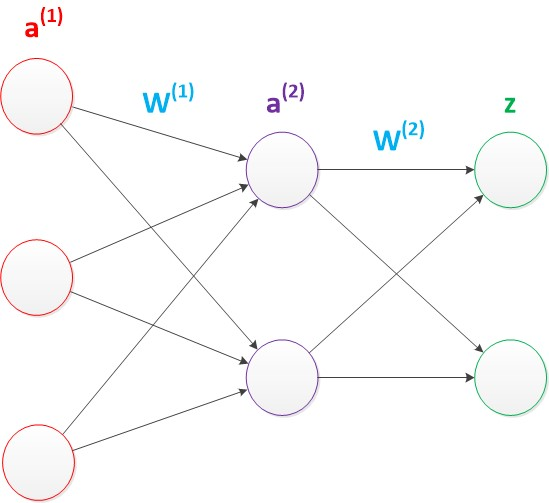
使用矩陣來進行向量化,a¹,a²,z是網路傳輸的向量資料，W¹和W²是網路的矩陣引數

a² = g(W¹a¹) 

z = g(W²a²)

由此可見，使用矩陣來向量化不會受到節點的數量影響，因此神經網路大量使用矩陣運算來描述。

偏置節點：它本質上是一個只函式儲存功能，切儲存值永遠為1的單元，除了輸出層外，神經網路的每個層都含有一個偏置單元，跟線性迴歸模型和邏輯(logistic)迴歸模型相同。

偏置單元與後一層的所有節點都有連線，設引數為向量b，稱為偏置

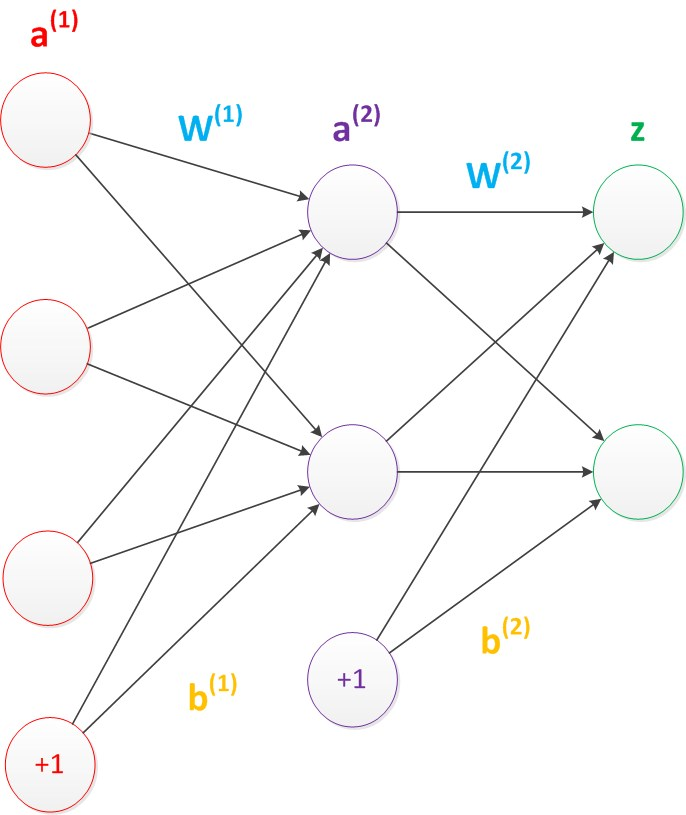
偏置節點沒有輸入，在考慮偏置後神經網路的矩陣運算：

a² = g(W¹a¹ + b¹) 

z = g(W²a² + b²)

g函式為sigmoid函式又稱logistic函式、啟用函式：g(x) = 1/(1+e^-x)，輸入大於0時輸出為1，小於0是輸出為0。

理論證明，兩層神經網路可以無限逼近任意連續函式

隱藏層的節點數設計

在設計一個神經網路是，輸入層的節點數需要與特徵的維度匹配，輸出層的節點數也要與目標的維度匹配，而隱藏層的節點數，由設計者指定，但是節點數設定多少，卻會影響模型的效果，如何決定這個自由層的節點數呢？目前業界沒有完善的理論來指導這個決策。一般是根據經驗來設定。較好的方法就是預先設定幾個可選值，通過切換這幾個值來看整個模型的預測效果，選擇效果最好的值作為最終選擇。這種方法又叫做Grid Search（網格搜尋）

瞭解了兩層神經網路的結構以後，我們就可以看懂其它類似的結構圖。例如EasyPR字元識別網路架構（下圖）。

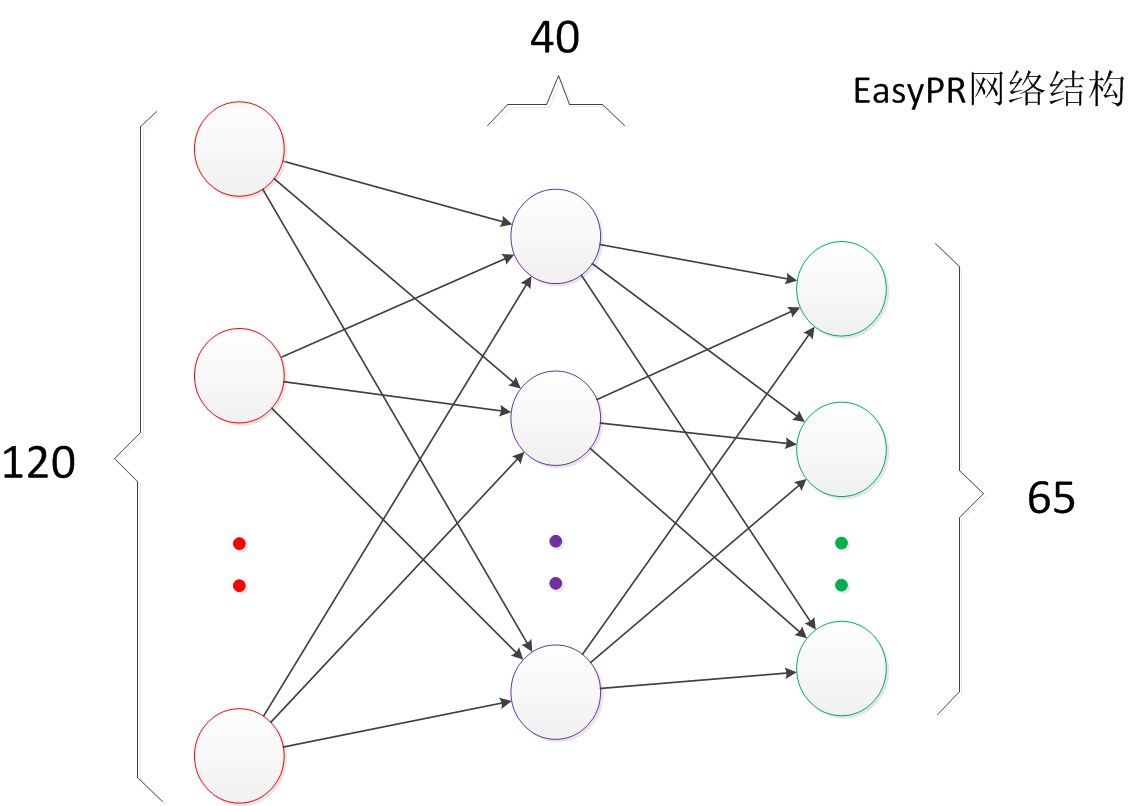
EasyPR使用了字元的影象去進行字元文字的識別。輸入是120維的向量。輸出是要預測的文字類別，共有65類。根據實驗，我們測試了一些隱藏層數目，發現當值為40時，整個網路在測試集上的效果較好，因此選擇網路的最終結構就是120，40，65。

參考：

1、《機器學習》(吳恩達)

2、計算機的潛意識：https://www.cnblogs.com/subconscious/p/5058741.html