Bobo老師機器學習筆記第八課-方差、偏差、嶺迴歸、LASSO迴歸?
對誤差分類
問題一、什麼是偏差和方差?
先看下面這幅圖圖:
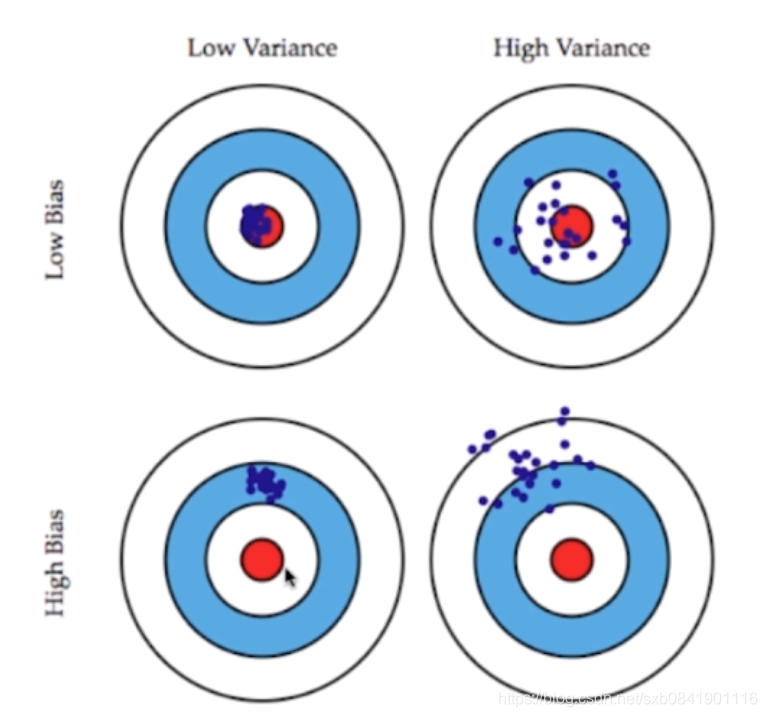
方差: 都是圍著資料中心的,方差越大則表示距離資料中心分佈的越分散,越小說明越近越集中
偏差: 偏離資料中心, 偏差越大,說明整個資料距離中心越遠,偏差越小,說明距離資料中心越近。
這兩者的關係通常是矛盾的,降低偏差會提高方差,降低方差會提高偏差。所有一個好的模型就是對這點的一個平衡。
二、模型誤差來自於哪些?
模型誤差 = 偏差(Bias)+ 方差(Variance) + 不可避免的誤差
造成偏差的原因:
1、對本身問題的假設不正確 (比如:非線性資料使用模型迴歸)
2、選取的特徵不對(比如評估學生的成績選用的名字)
造成方差的原因:
1、資料的一點點抖動
2、通常情況,模型比較複雜(高階線性迴歸)
三、哪些演算法是高方差,哪些演算法是高偏差?
3.1 有一些演算法天生是高方差的演算法,如KNN,因為KNN對資料的抖動比較明顯
3.2 非引數學習通常都是高方差演算法,因為不對資料進行任何假設
3.3 有一些演算法天生是高偏差演算法,比如線性迴歸。
3.4 引數學習通常是高偏差演算法,因為堆資料有很強的假設。
問題四、在機器學習領域,主要學習的挑戰主要來自於方差。那麼如何降低方差呢?
4.1 降低模型的複雜度
4.2 降低資料維度,降噪
4.3 增加樣本 (針對於多引數情況)
4.4 使用驗證集
4.5 模型的正則化
問題五、什麼是模型正則化(Regularization)?
問題五、什麼是模型正則化(Regularization)?
首先我們看一下過擬合的曲線。 存在過擬合也就意味著特徵值的前面引數可能過大。 為了避免這種情況,那麼在模型訓練的時候可以通過一些手段對於引數進行一些限制。 模型正則化就是要做這個事情,通過一些方法限制引數的大小。 換句話說,使某些係數的估計為0。主要用來解決 多重共線性問題(引數相關)
主要收縮方法主要包括 嶺迴歸(ridge regression)和 LASSO迴歸
問題六、什麼是嶺迴歸?
首先看過擬合的情況:
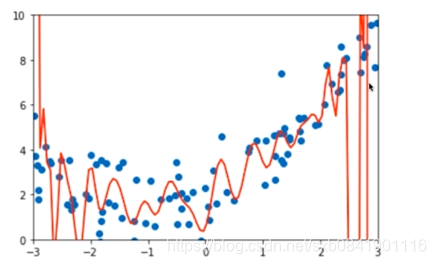
我們知道這種情況是由於過擬合,也就是計算的theta引數太大了。那我們自然就想到如何讓theta的取值最小。 簡單的辦法就是讓所有theta的平方和最小。損失函式有如下變化:

通過上面公式可以看出,就是在原來基礎上新增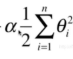 這部分函式。這種方式叫嶺迴歸。 這個函式一般稱為懲罰函式, 其中 alpha是一個超引數,這個引數越大就表示懲罰函式在目標函式中佔得比例越大。
這部分函式。這種方式叫嶺迴歸。 這個函式一般稱為懲罰函式, 其中 alpha是一個超引數,這個引數越大就表示懲罰函式在目標函式中佔得比例越大。
至於為什麼要加入這個項,這裡面涉及到一些線性代數的知識,大家可以參考下面文章。
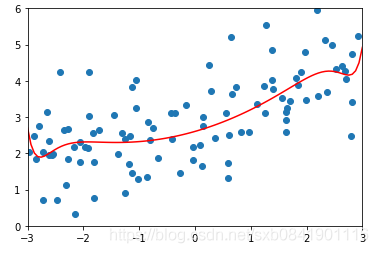
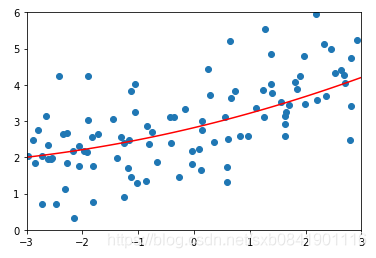
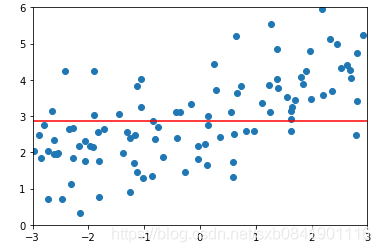
![]() 分別取0.0001, 1, 100的圖形如下(從左到右):
分別取0.0001, 1, 100的圖形如下(從左到右):
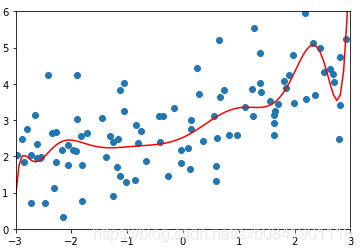
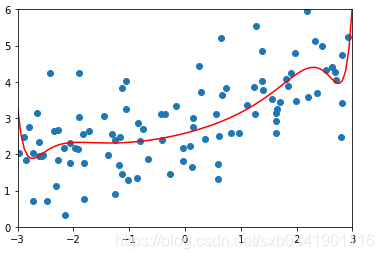
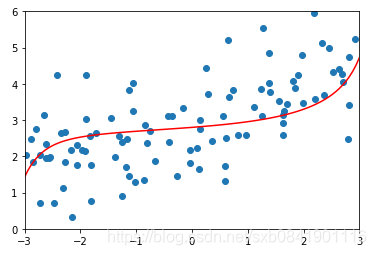
可以看出隨著![]() 值越大,曲線越來越平滑。那麼這個值多少是合適呢,這個要結合實際的資料看。一般而言,嶺迴歸的引數在0.0001~1之間。在sklearn中預設的是1
值越大,曲線越來越平滑。那麼這個值多少是合適呢,這個要結合實際的資料看。一般而言,嶺迴歸的引數在0.0001~1之間。在sklearn中預設的是1
問題七、什麼是LASSO迴歸?
什麼是LASSO迴歸?
首先LASSO是Least Absolute Shrinkage and Selection Operator的縮寫。 相對於嶺迴歸的公式:
![]()
在嶺迴歸的懲罰函式是均方差,而LASSO迴歸是絕對值。 嶺迴歸就是調整引數前面的引數, 而LASSO迴歸就直接把引起共線的變數前面的引數設定為0. 對比嶺迴歸:
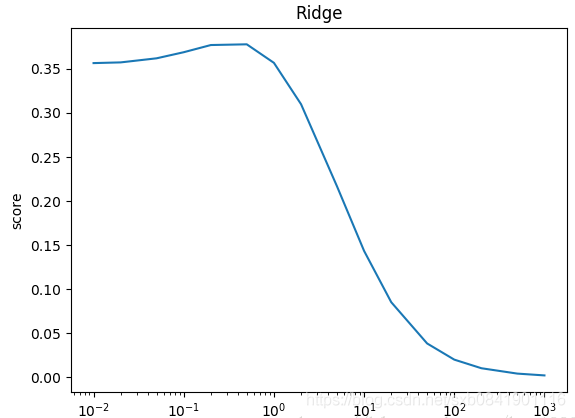
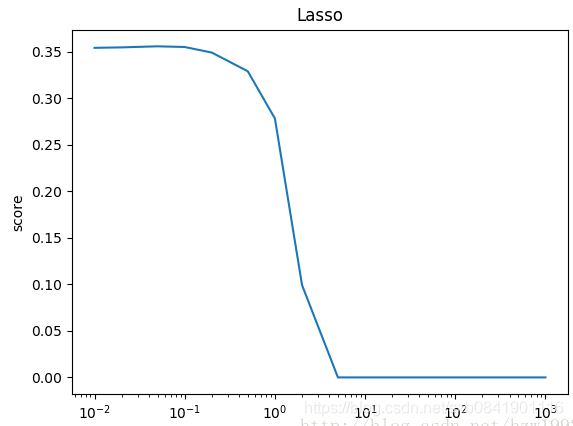
可以看到,Lasso迴歸最終會趨於一條直線,原因就在於好多θ值已經均為0,而嶺迴歸卻有一定平滑度,因為所有的θ值均存在。
![]() 分別取0.01, 0.1, 1的圖形如下(從左到右):
分別取0.01, 0.1, 1的圖形如下(從左到右):
可以看出在LASSO迴歸中,![]() 取值一般偏小,mean_squared_error最小的時候在0.01.
取值一般偏小,mean_squared_error最小的時候在0.01.
問題八、LP範數與嶺迴歸、LASSO迴歸有什麼聯絡?
表達形式: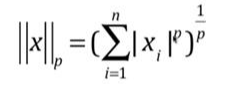 ,其中X是矩陣, 前面就是X的模。
,其中X是矩陣, 前面就是X的模。
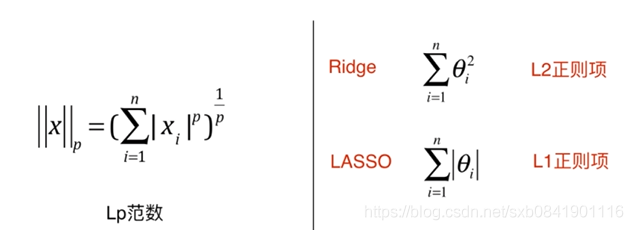
如果把這兩種結合起來,就是彈性網, ElasticNet
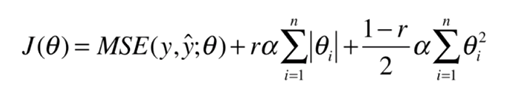
在實際應用中,一般首先嚐試L2正則項, 但如果特徵量太大了,那麼計算會比較複雜,這個時候考慮使用彈性網。最後考慮LASSO,因為LASSO會把一些引數設定為0,容易形成計算錯誤,導致我們漏掉了一些重要的引數。
參考文章: