問題1: 什麼是多項式迴歸？

以前我們學習了線性迴歸，但是線性迴歸比較適用於資料之間明顯線性關係的。但有時我們使用的資料不一定它們之間有線性關係。那麼這時候就要用到多項式迴歸。多項式我們以前學過，那麼多項式的迴歸方程就類似於

問題2: 那麼非線性的資料，我們如何做呢，比如下面資料？

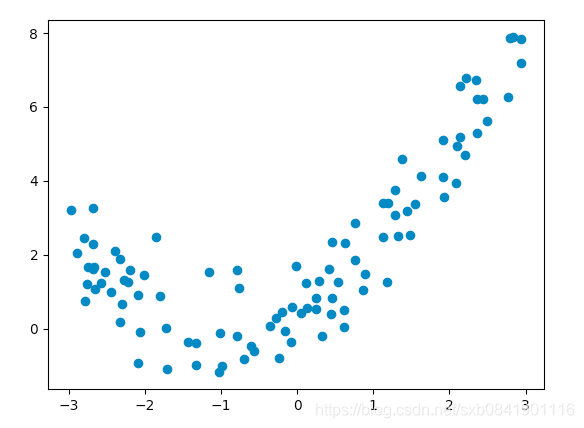
如果利用上面的資料我們進行線性迴歸，結果是下面的

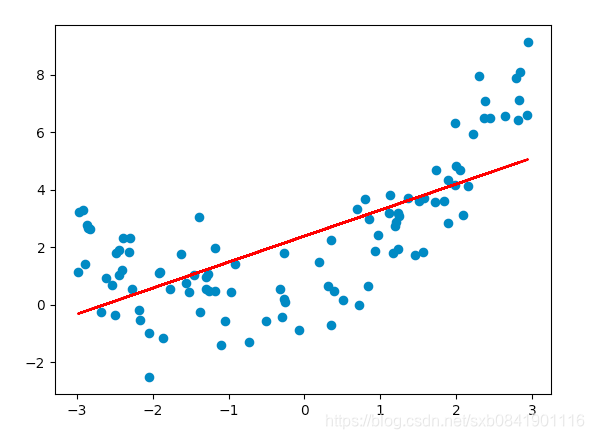
通過上圖可以看出來，上面這條直線對資料迴歸不太好。迴歸的準確率也是50%。明顯這個效果是不太理想的。 

針對這種情況，應該如何處理呢？ 

由於這個資料我們大概能看出來是一個2次方的。所以我們可以原來基礎資料上X在增加一個特徵X**X。 

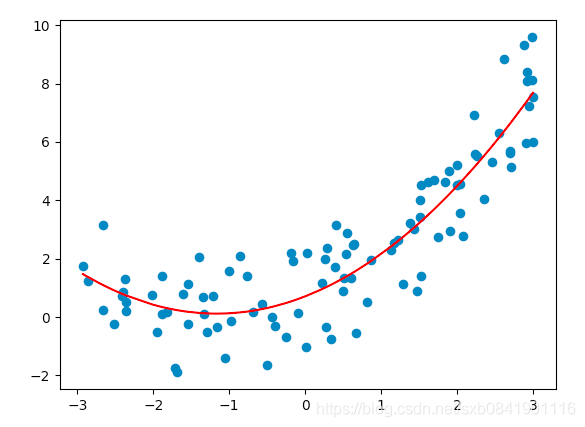
很顯然上圖迴歸的效果要好的多, 我們看看引數：

0.5758300432861141 [0.91972786 0.52439824] 

截圖是0.57， X的係數是0.9， X**2的係數是0.5。 

這個係數和我們最初設定引數（y = 0.5 * x ** 2 + x + 0.6 + np.random.normal(0, 1., size=100)  ）和相近。

問題3： 在上圖中，我們增加了一個特徵，從而使得一維升級到二維資料。但是在日常的資料中，我們又怎麼知道是新增一個特徵值還是多個特徵值了，並且我們如何新增的這個特徵的值是什麼呢？ 

在這裡sklearn給我提供了一個方法，

from sklearn.preprocessing import PolynomialFeatures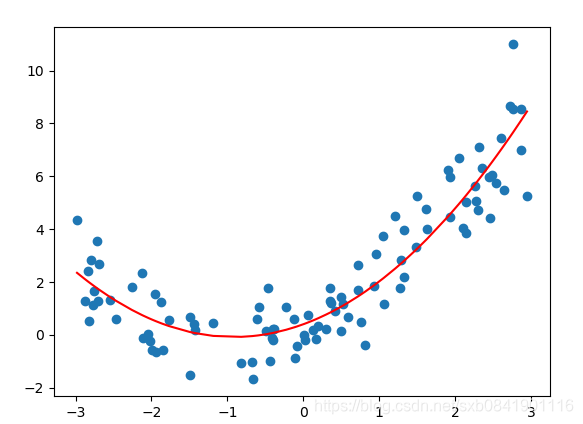

通過繪圖可以看到，利用polynomialfeature處理的資料訓練的結果和我們預期的相同。

訓練的結果：(0.6407352027144722, array([0.        , 0.9814608 , 0.47231414]))

0.6是截距，0是因為經過polynomialfeature處理會在增加首列為1.下文可以看到。 0.98和0.47是我們要求的引數
('X.shape:', (100L, 1L))
('X_ploy.shape:', (100L, 3L))
[[ 0.07775644]
 [-1.77960351]]
[[ 1.          0.07775644  0.00604606]
 [ 1.         -1.77960351  3.16698866]]

執行結果中可以看出：

1、 X原先是100x1的矩陣，經過處理變成100x3的矩陣。打印出前2行，可以通過經過多項式處理後的資料增加了兩列。

第一列是常數1，第三列是原來資料的平方。為什麼是平方？ 因為輸入的矩陣只有1列，所有是按照X的0次冪，X的1次冪，X的次冪。如果是2列（a, b）結果就是[1, a, b, a^2, ab, b^2] 。 預設degress=2。

本例子中例項程式碼：

# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.model_selection import P

x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x ** 2 + x + 0.6 + np.random.normal(0, 1., size=100)

# 簡單繪製測試資料
'''

reg = LinearRegression()
reg.fit(X, y)
plt.scatter(x, y)
plt.show()
'''

# 方法一 增加一個X**2的特徵

'''
reg = LinearRegression()
X2 = np.hstack([X, X ** 2])
reg.fit(X2, y)
y_predict = reg.predict(X2)
print (reg.intercept_, reg.coef_)
plt.scatter(x, y)
# 此處要注意，要根據X從小到大進行排序
plt.plot(np.sort(x), y_predict[np.argsort(x)], color='red')
plt.show()
'''

# 使用PolynomialFeatures

poly = PolynomialFeatures()
poly.fit(X)
X_ploy = poly.transform(X)
reg = LinearRegression()
reg.fit(X_ploy, y)
y_predict = reg.predict(X_ploy)
print ( reg.intercept_, reg.coef_)
print ('X.shape:',X.shape)
print('X_ploy.shape:', X_ploy.shape)
print (X[:2, :])
print(X_ploy[:2, :])
plt.scatter(x, y)
# 此處要注意，要根據X從小到大進行排序
plt.plot(np.sort(x), y_predict[np.argsort(x)], color='red')
plt.show()

參考文章：

【機器學習】多項式迴歸 

要是你在西安，感興趣一起學習AIOPS，歡迎加入QQ群 860794445