【3.x】

    將數學類 CCPoint、CCRect 改為v3.x版本的 Vec2、Rect 就好了。

【簡單碰撞檢測】

    在一些遊戲中經常會遇到碰撞檢測的情況，如憤怒的小鳥飛出去後，是否與石頭髮生碰撞。

    雖然說有一個Box2D物理碰撞引擎，但是在這裡還是需要掌握一下簡單的碰撞檢測方法。

    （1）矩形與矩形

    （2）圓與圓

    （3）矩形與圓

1、矩形與矩形

    1.1、提出問題

    問題：假設有兩個矩形rect1，rect2，判斷兩矩是否碰撞相交（部分割槽域重疊）。

    如下四幅圖中，圖1、2、4發生碰撞，圖3未發生碰撞。

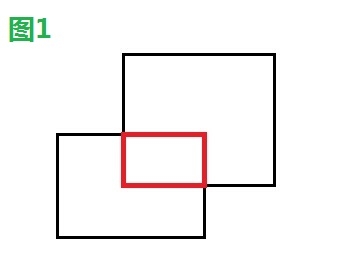
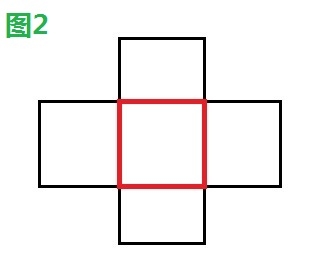
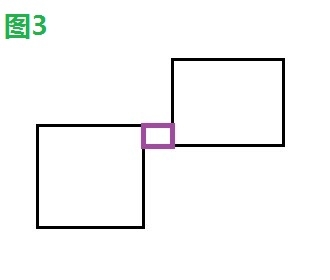
    1.2、解決方案

    由圖可知，判斷方法只要計算一下兩個矩形相交部分是否能夠成一個小矩形。

    判斷方法如下：（可用於計算相交部分的小矩形資訊）

//
	bool collision_RectWithRect(CCRect rect1, CCRect rect2)
	{
	//計算相交部分的矩形
	//左下角座標：( lx , ly )
	//右上角座標：( rx , ry )
		float lx = max(rect1.getMinX() , rect2.getMinX() );
		float ly = max(rect1.getMinY() , rect2.getMinY() );

		float rx = min(rect1.getMaxX() , rect2.getMaxX() );
		float ry = min(rect1.getMaxY() , rect2.getMaxY() );

		//判斷是否能構成小矩形
		if( lx > rx || ly > ry ) return false; //矩形不相交
		else                     return true;  //發生碰撞
	}
//
 

    當然也可以使用cocos2dx引擎中的CCRect類已經存在的一個判斷矩形碰撞的函式。

//
	//返回bool。相交為true
	rect1.intersectsRect(rect2);
//
	
//	
	//intersectsRect()函式的原始碼如下：
	bool CCRect::intersectsRect(const CCRect& rect) const
	{
		return !(     getMaxX() < rect.getMinX() ||
				 rect.getMaxX() <      getMinX() ||
					  getMaxY() < rect.getMinY() ||
				 rect.getMaxY() <      getMinY());
	}
//
 

2、圓與圓

    2.1、提出問題

    問題：假設有兩個圓circle1，circle2，判斷兩圓是否碰撞相交（部分割槽域重疊）。

    如下三幅圖中，圖1、2發生碰撞，圖3未發生碰撞。

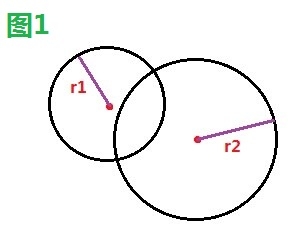
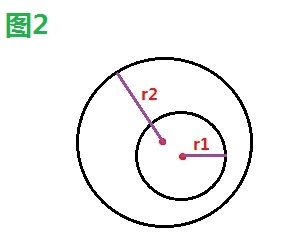
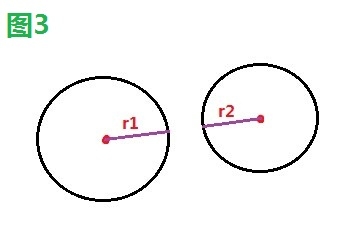
    2.2、解決方案

    圓的碰撞檢測比較簡單，只要判斷兩圓心距離是否小於半徑相加（r1+r2）即可。

    判斷方法如下：

//
	bool collision_CircleWithCircle(CCPoint p1, float r1, CCPoint p2, float r2)
	{
	//計算圓心距離
		float dist = p1.getDistance(p2);

	//判斷兩圓是否相交
		return dist < (r1+r2) ;
	}
//

3、矩形與圓

    3.1、提出問題

    問題：假設有矩形rect、圓circle，判斷矩形和圓是否碰撞相交（部分割槽域重疊）。

    如下四幅圖中，圖1、2、4發生碰撞，圖3未發生碰撞。

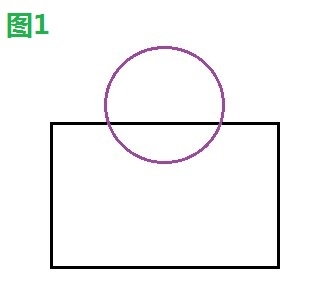
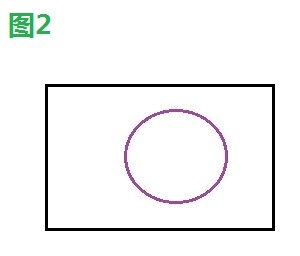
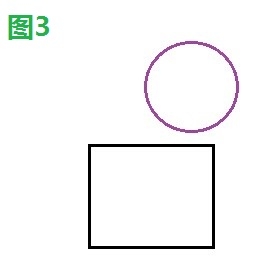
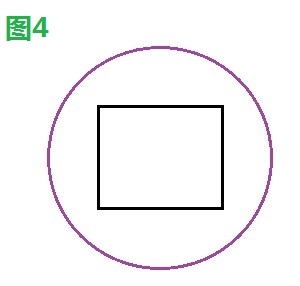
    3.2、解決方案

    矩形和圓的判斷比較複雜，請看以下分析。

    （1）首先，我們讓圓在矩形外沿著矩形的邊滾一圈，然後將圓心移動的軌跡連線，就可以得到一個圓角矩形。

    （2）如下圖紅色區域為圓角矩形，顯然我們只要判斷圓心是否在圓角矩形區域內部即可。

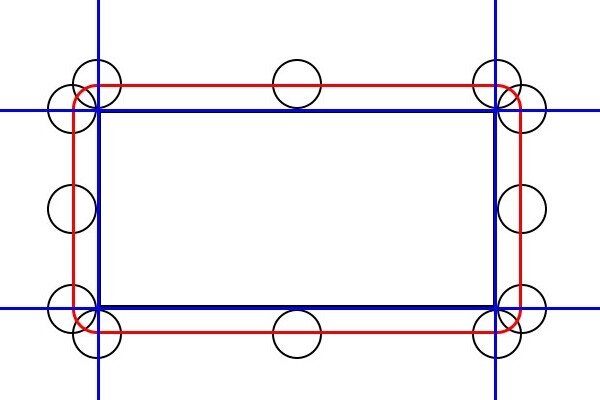
  （3）如果除去圓角矩形四個角上的4個四分之一圓的部分，僅僅讓你判斷圓心是否落在剩下的區域內，你應該能很快想出解決辦法吧？

        只要判斷圓心是否在兩個矩形的任意其中之一的內部即可。

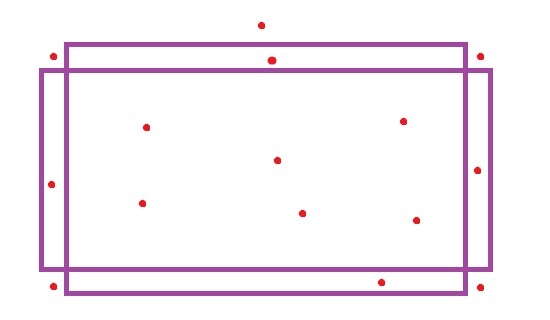
    （4）然後再判斷圓心是否在四個角上的四分之一圓的區域部分即可。

        顯然，只要判斷圓心與矩形的四個頂點的距離是否小於圓的半徑即可。

    （5）綜合上訴：（3）（4）的判斷，即可得出圓是否矩形相交。

    判斷方法如下：

//
	bool collision_RectWithCircle(CCRect rect, CCPoint p, float r)
	{
	//獲取矩形資訊
	//左下角座標：( lx , ly )
	//右上角座標：( rx , ry )
		float lx = rect.getMinX();
		float ly = rect.getMinY();
		float rx = rect.getMaxX();
		float ry = rect.getMaxY();

	//計算圓心到四個頂點的距離
		float d1 = p.getDistance( ccp(lx, ly) );
		float d2 = p.getDistance( ccp(lx, ry) );
		float d3 = p.getDistance( ccp(rx, ly) );
		float d4 = p.getDistance( ccp(rx, ry) );

	//判斷是否碰撞
		//判斷距離是否小於半徑
		if( d1<r || d2<r || d3<r || d4<r ) return true;
		//是否在圓角矩形的，橫向矩形內
		if( p.x > (lx-r) && p.x < (rx+r) && p.y > ly && p.y < ry ) return true;
		//是否在圓角矩形的，縱向矩形內
		if( p.x > lx && p.x < rx && p.y > (ly-r) && p.y < (ry+r) ) return true;

	//不發生碰撞
		return false; 
	}
//