關於GANs原論文裡的數學證明

阿新 • • 發佈：2018-12-09

GANs的核心理念很簡單，其實就是回答了最大似然估計沒有辦法解決的問題提出另一條解決路徑。所以在全面認識GANs之前首先需要掌握一點點最大似然相關的知識。

這個文章主要是根據最近做的一個PPT進行相關的講解註釋。

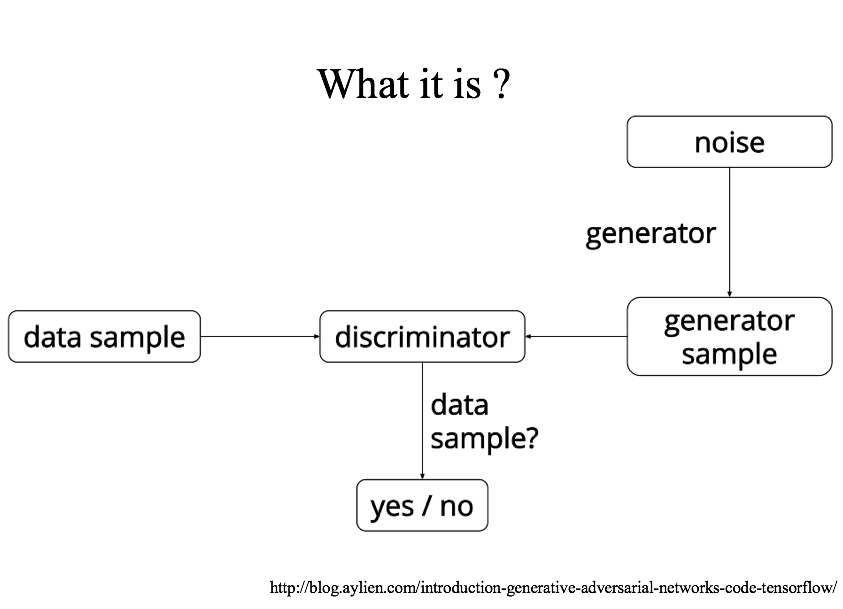
首先我們講下什麼是GANs，從最簡單的流程圖從上往下看就是，首先定義一些噪音資料（這裡我更偏向於稱作種子資料。anyway），將他們喂(feed)給生成器，經由生成器後最初的一些噪音資料會得到相應的，具有一定分佈形式的資料，之後分別將生成的資料和真實資料交給判別器，判別器的主要作用就是根據這些資料的相關特性來分辨這些資料中哪些是來源於真實資料，哪些是來源於生成器構造的資料。這個可以看作是GNAs的單次運算過程。

具體來說GANs是怎麼工作的呢？其實在原論文中作者就有過相關的詳細描述。這裡做個簡單的翻譯。為了讓p_g(構建的資料)最終能符合真實資料的分佈，我們首先將一些毫無規律的噪音資料輸入到生成器中，生成器根據喂進的資料生成具有一定分佈形式的資料G(z,Θ)，同時我們還定義了一個判別器D(x)，其輸出為單個標量。判別器D的主要功能就是判別輸入其中的資料是否來自於真實的資料集中而不是來自構建的資料集中。訓練判別器D使其對兩個來源的資料能最準確的判別，例如來源於真實資料集的資料經過判別器的判斷其概率接近於1，而來源於構建資料集中的資料經過判別器的判斷，其概率更接近於0。從而將兩種來源的資料劃分開來。

這幾個圖從真實資料集的分佈，構建的資料分佈以及判別器的判別線這三個元素動態的展示了GANs運算優化過程，並且可以在最後一張圖中看出最終達到最優解時判別器對兩種來源的資料判斷的概率均為0.5，且構建的資料已經和真實資料的分佈重合，表示此時，判別器已經無法二者的差別。本文後面部分將主要從數學角度依據原論文中的相關公式計算驗證這一最優解的情況是否具有嚴格的資料驗證。

文中給出的演算法示例，其大致過程與上述描述的一致，只是在其中補充了更新判別器D和生成器G的策略，分別是應用隨機梯度上升優化D，用隨機梯度下降來優化更新生成器。

接下來就是一堆數學相關的驗證時刻了，這個公式是原文中的第一個公式，有江湖傳言，如果一眼就能看懂這個公式在講些什麼，就說明你的GANs已經達到大成的級別了～首先我們來說說開頭部分的那個minmax，它是源自博弈論中的極小極大博弈來的，簡單的說就是在函式V(D, G)中D和G兩者之間形成了一種此消彼長的關係。所謂的極小極大就是指，D和G兩者的作用（G和D更準確點）。就是說D的主要作用是要將函式值拖向極大那邊，而G的作用就是要將函式值怒力拖向極小的那邊。其中E_x~pdata

(x)[log D(x)]公式中的這種形式，很大程度上是來源於對數似然函式（個人猜測，但也挺合理的）。

這一頁就是最大似然函式的相關知識，主要參考了李巨集毅18年講解的GANs課程PPT，只是將其中的英文部分翻譯成了中文而已，後面還有幾張片子也是來源於他的課程PPT之中的。

這個片子也是參照李巨集毅的課程PPT，與他不同的是我在這裡並沒有關注他原版PPT中將似然函式與KL散度統一的那塊知識，主要是覺得目前還不太會干擾到我後續對GANs論文數理部分的理解，首先這上面取log的主要原因是將連乘轉化成加法運算，並且在取完log之後對本來的函式也沒有什麼本質上的性質改變（這一點很重要！），所以可行。最後一步的約等於是大數定理已經證明的結論，即，當M接近無限大時，可以用期望乘以log(…)代替將log(…)求和。

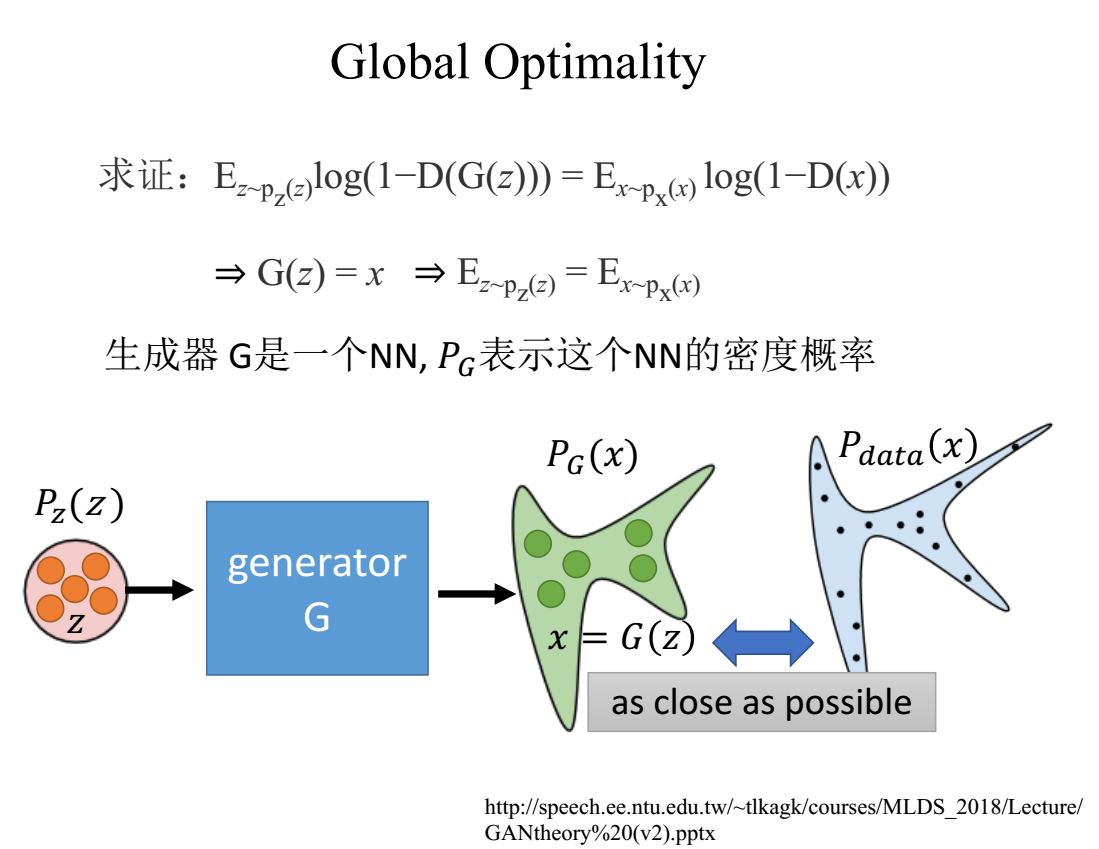
為什麼要求證圖中的式子，因為這個等式成立對我很重要（其實是，這個等式成立是後面幾步運算的基礎）。這裡依然採用李巨集毅PPT中的解釋，（目前來說看到的大部分相關部落格對這一部分要不就是沒有解釋，要不就是採用了我下張片子會講到的驗證方法，但也很少有涉及的部落格）這裡主要是一個理解的過程，第一個等式成立代表了G(z) = x；同時E_z = E_x也是成立的。這一步的基礎是在給定的G 的基礎上求解D的最優解（這是大前提）。具體按圖中的意思就是經過一段優化之後（論文以及後續的很多實驗都說最好預先訓練G一小會）生成器G可以將吃掉的噪音資料大致的規劃成一個新的分佈，就是P_G(x), G吃掉的z生成的就是x(這個x不是來源於真實資料集的x而是生成器生成的x)，GANs做到後面就是要讓兩種來源的x達到幾乎一樣分佈的地步，是判別器無法區分。