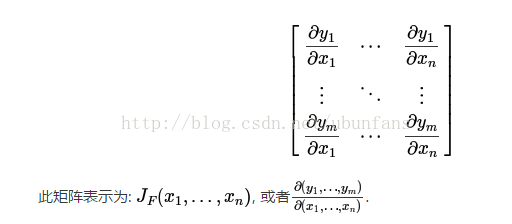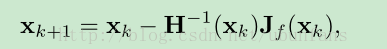一般來說, 牛頓法主要應用在兩個方面, 1, 求方程的根; 2, 最優化。

1，求方程的根

其原理便是使用泰勒展開，然後去線性部分，即：

                (1)  (得到的是x在x0附近的一階線性方程，即下圖中那條切線)

然後令上式等於0，則有： (令其為0即切線與x軸交點)

                                (2)

經過不斷迭代：

                             (3)

當精度達到要求的時候停止迭代。

迭代示意圖如上所示。

2，最優化

最優化一般是求極大或極小問題，這可以轉變為求導數零點，然後轉變為1的情形。

即f' = 0;

把f(x)用泰勒公式展開到二階，即：

                                          (4)

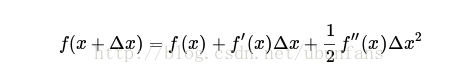
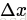
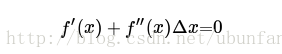
等號左邊和f(x)近似相等，抵消。然後對求導，得到：

                                                                           (5)

更進一步：

                                                                                (6)

然後得到迭代式子：

                                                            (7)

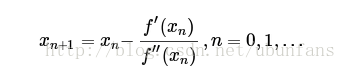
以上只針對單變數進行討論，如果對多變數就要引入雅克比矩陣和海森矩陣

簡單介紹一下二者，雅克比矩陣為函式對各自變數的一階導數，海森矩陣為函式對自變數的二次微分。形式分別如下：

把兩個矩陣代入(7)中

參考文獻：