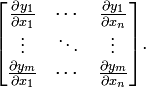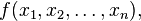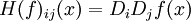雅可比矩陣 和 海森矩陣
雅可比矩陣
假設F:Rn→Rm 是一個從歐式n維空間轉換到歐式m維空間的函式。這個函式由m個實函式組成: y1(x1,...,xn), ..., ym(x1,...,xn). 這些函式的偏導數(如果存在)可以組成一個m行n列的矩陣,這就是所謂的雅可比矩陣:
此矩陣表示為:
-
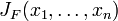 ,或者
,或者 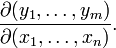
這個矩陣的第i行是由梯度函式的轉置yi(i=1,...,m)表示的
在數學中,海森矩陣(Hessian matrix 或 Hessian)是一個自變數為向量的實值函式的二階偏導數組成的方塊矩陣,此函式如下:
如果 f 所有的二階導數都存在,那麼 f 的海森矩陣即:
其中 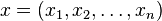 ,即
,即
相關推薦
轉載大神的對雅可比矩陣和海森矩陣的講解
1. Jacobian 在向量分析中, 雅可比矩陣是一階偏導數以一定方式排列成的矩陣, 其行列式稱為雅可比行列式. 還有, 在代數幾何中, 代數曲線的雅可比量表示雅可比簇:伴隨該曲線的一個代數群, 曲線可以嵌入其中. 它們全部都以數學家卡爾·雅可比(Carl Jacob, 1804年10月4日-1851
雅可比矩陣 和 海森矩陣
雅可比矩陣 假設F:Rn→Rm 是一個從歐式n維空間轉換到歐式m維空間的函式。這個函式由m個實函式組成: y1(x1,...,xn), ..., ym(x1,...,xn). 這些函式的偏導數(如果存在)可以組成一個m行n列的矩陣,這就是所謂的雅可比矩陣: 此矩陣表
雅克比矩陣和海森矩陣 Jacobian and Hessian Matrix
轉:http://jacoxu.com/jacobian%E7%9F%A9%E9%98%B5%E5%92%8Chessian%E7%9F%A9%E9%98%B5/ 1. Jacobian 在向量分析中, 雅可比矩陣是一階偏導數以一定方式排列成的矩陣, 其行列式稱為雅可比行列式. 還有, 在代
雅克比矩陣、海森矩陣與非線性最小二乘間的關係與在SFM和Pose Estimation中的應用
近期,在研究SFM和pose estimation時時常接觸到這三個詞,剛開始不太明白他們間的關係,現將他們整理一下。歡迎吐槽,有什麼不對的地方歡迎指正! 首先,介紹一下三個詞的數學定義與含義: 雅可比矩陣 假設F:Rn→Rm 是一個從歐式n維空間轉
牛頓法、雅克比矩陣、海森矩陣
一般來說, 牛頓法主要應用在兩個方面, 1, 求方程的根; 2, 最優化。 1,求方程的根 其原理便是使用泰勒展開,然後去線性部分,即: (1) (得到的是x在x0附近的一階線性方程,即下圖中那條切線) 然後令上式等於0,則有:
深度模型從研者 眼裡的 似然估計 & Hessain 海森矩陣 & Fisher Information (費雪資訊)
深度模型的訓練的基本依據是最小化模型擬合數據的誤差。旨在不僅知其然(如何構建和訓練一個深度模型),還應知其所以然(為什麼這樣訓練,可以做哪些優化)。我們就會發現,有很多研究者,在面向一些特定問題下,深度模型訓練演算法中的誤差函式定義也就有很多種。而萬變不離其宗,如果想
【影象處理】海森矩陣(Hessian Matrix)及一個用例(影象增強)
前言 Hessian Matrix(海森矩陣)在影象處理中有廣泛的應用,比如邊緣檢測、特徵點檢測等。而海森矩陣本身也包含了大量的數學知識,例如泰勒展開、多元函式求導、矩陣、特徵值等。寫這篇部落格的目的,就是想從原理和實現上講一講Hessian Matr
雅克比矩陣 海森矩陣 牛頓法
雅可比矩陣是以一階偏導數以一定方式排列成的矩陣,其行列式稱為雅可比行列式。 雅可比矩陣的重要性在於它體現了一個可微方程與給出點的最優線性逼近。因此,雅可比矩陣類似於多元函式的導數。 海森矩陣是一個以自變數為向量的實值函式的二階偏導陣列成的方塊矩陣。 此函式如下,f(
CNN輸出每一層的卷積核,即每一層的權重矩陣和偏移量矩陣
var 圖像 cas 值轉換 auth git dom 轉換 訓練 分別是16個5*5的一通道的卷積核,以及16個偏移量。A2是轉置一下,為了輸出每一個卷積核,TensorFlow保存張量方法和人的理解有很大區別,A21 A31 A41 A51都是卷積核的權重矩陣偏移量
協方差矩陣和相關係數矩陣(R語言)
一、協方差矩陣 1.協方差定義 &n
【1.1】Eigen C++ 矩陣開源庫學習之稠密矩陣和陣列操作——矩陣類
稠密矩陣和陣列操作 http://eigen.tuxfamily.org/dox-devel/group__DenseMatrixManipulation__chapter.html 包含模組: 1.矩陣類 2.矩陣和向量的運算
雅可比矩陣和Hessian矩陣
1. Jacobian 在向量分析中, 雅可比矩陣是一階偏導數以一定方式排列成的矩陣, 其行列式稱為雅可比行列式. 還有, 在代數幾何中, 代數曲線的雅可比量表示雅可比簇:伴隨該曲線的一個代數群, 曲線可以嵌入其中. 它們全部都以數學家卡爾·雅可比(Carl Jacob, 1804年10月4日-
matlab 雅可比矩陣求取
syms x1 x2 ;%定義變數 a = [x1 x2]; f = [x1*x1+t*x1;x2*cos(x2)]; %定義函式,以矩陣的形式 x = jacobian(f,a); % 求取雅可比矩陣,會發現x是sym型別的 b = [1 2]; y = subs(x,a,b); %賦值 %此
OpenGL ES平移矩陣和旋轉矩陣的左乘與右乘效果
角度 style 位置 作用 span 坐標系 rotate 不同的 世界 OpenGL ES平移矩陣和旋轉矩陣的左乘與右乘 在OpenGL 、OpenGL ES中矩陣起著舉足輕重的作用,而矩陣之間的左乘與右乘在效果上是不同的。 一、先平移後旋轉 場景效果:人繞樹旋轉。 原
線性代數-矩陣-【5】矩陣化簡 C和C++實現
tar tput c++ spec 但是 exc c++語言 emp opened 點擊這裏可以跳轉至 【1】矩陣匯總:http://www.cnblogs.com/HongYi-Liang/p/7287369.html 【2】矩陣生成:http://www.cnblog
#6030. 【雅禮集訓 2017 Day1】矩陣
line 字符 oid inline 技術分享 任務 有一種 run -h #6030. 「雅禮集訓 2017 Day1」矩陣 題目描述 有一個 n×n 的矩
hihocoder 1580 dp最大子矩陣和
ima freopen tdi com hihocode images namespace ans open 題意: 給出n*m的矩陣求最大子矩陣和,要求必須把矩陣中的某一個元素替換成p 代碼: //求最大子矩陣和,容易想到壓縮之後dp但是這道題要求必須替換一
【算法】Dijkstra算法(單源最短路徑問題) 鄰接矩陣和鄰接表實現
當前 prior 排序 發的 單源最短路徑 fine emp eat col Dijkstra算法可使用的前提:不存在負圈。 負圈:負圈又稱負環,就是說一個全部由負權的邊組成的環,這樣的話不存在最短路,因為每在環中轉一圈路徑總長就會邊小。 算法描述: 1.找到最
Spark機器學習中ml和mllib中矩陣、向量
int reg index mac matrix 對比 判斷 bsp ive 1:Spark ML與Spark MLLIB區別? Spark MLlib是面向RDD數據抽象的編程工具類庫,現在已經逐漸不再被Spark團隊支持,逐漸轉向Spark ML庫,Spark ML是面
周任務——矩陣和行列式
dsa 相等 一個 復數 分享 bsp ddl 分享圖片 ec2 話說我一個初二的小蒟篛,給我布置線性代數(汗)。。。。。。 矩陣 第一部分 矩陣的定義 由 m × n 個數aij排成的m行n列的數表稱為m行n列的矩陣,簡稱m × n矩陣。記作: 這m×n 個數稱