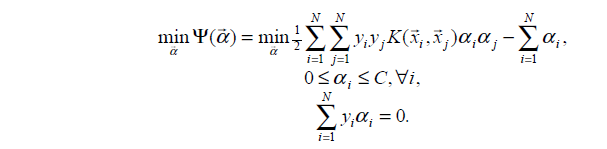2. 程式人生 > >SMO演算法理解

SMO演算法理解

阿新 • • 發佈：2018-12-11

SMO演算法看了近3遍感覺還是有點朦朦朧朧，模模糊糊。

所以索性，理解多少寫多少，避免遺忘。可能會有很多錯誤，歡迎指正。

主要基於李航的《統計學習方法》

SMO(sequential minimal optimization)序列最小最優化演算法

我們在討論支援向量機的學習問題時，可以將其轉換成求解凸二次規劃問題。實現支援向量機的學習是要找到這樣的凸二次規劃問題的全域性最優解，SMO就是支援向量機學習的一種快速演算法，也是一種啟發式演算法。

基本思路：

如果所有變數的解都滿足此優化問題的KKT條件，那麼這個最優化問題的解就得到了。(KKT條件是該最優化問題的充分必要條件)。否則，選擇兩個變數，固定其他變數，針對這兩個變數構建一個二次規劃問題。子問題的兩個變數，一個是違反KKT條件最嚴重的那一個，另一個由約束條件自動確定。如此，SMO演算法將原問題不斷分解為子問題求解，進而達到求解原問題的目的。[1]

特點：

將原始的二次規劃問題分解為只含有兩個變數的二次規劃子問題，對子問題不斷求解，使得所有的變數滿足KKT條件

包含兩部分：

1、求解兩個變數二次規劃的解析方法

2、選擇變數的啟發式方法

 

SMO演算法要解的是如下凸二次規劃的對偶問題：

其中，K( ，)是核函式

 

兩個變數二次規劃的求解方法

1、SMO的最優化問題的子問題

前面提到將原始的二次規劃問題分解為只含有兩個變數的二次規劃子問題，所以假設選定兩個變數\alpha_{1}、\alpha _{2}，其他變數相當於常數，省略常數後，SMO的最優化問題的子問題可以化簡成以下形式：

最終的優化目標是：

 ………… (1)

原來的約束條件變成：

s.t.  \alpha _{1}y_{1}+\alpha _{2}y_{2}=-\sum_{i=3}^{N}\alpha _{i}y_{i}=\xi （用\xi表示）…………(*)

還有0\leq \alpha _{i}\leq C

（注意，對於式子\alpha _{1}y_{1}+\alpha _{2}y_{2}=-\sum_{i=3}^{N}\alpha _{i}y_{i}=\xi，我們在用\alpha _{1}表示\alpha _{2}時，等式兩邊同時乘y _{1}就可以，不要用除以y _{1}的方式，要時刻記住y _{1}^{^{2}}=1）

 

2、視為一元函式，求導取極值

(1)式可以看成是一個二元函式，根據於\alpha _{1}和\alpha _{2}的約束關係，可以把\alpha _{1}消去。不過我們的目的是為了關於\alpha _{2}求導，導數為0的點就是要找的極值點，所以這裡既可以把\alpha _{1}消去後對\alpha _{2}求導，也可以直接在現在這個式子上對\alpha _{2}求導。

根據(*)式得

…………(2)

代入(1)式中，可以看成是一個一元函式

用w(\alpha _{1},\alpha _{2})來表示最優化的目標，將\alpha _{1}=(\xi -y_{2}\alpha _{2})y_{1}帶入得到

w(\alpha _{2})=\frac{1}{2}K_{11}(\xi -\alpha _{2}y_{2})^{2}+\frac{1}{2}K_{22}\alpha _{2}^{2}+y_{2}K_{12}(\xi -\alpha _{2}y_{2})\alpha _{2}-(\xi -\alpha _{2}y_{2})y_{1}-\alpha _{2}+v_{1}(\xi -\alpha _{2}y_{2})+y_{2}v_{2}\alpha _{2}

對上式中的\alpha _{2}求導等於0

…………(3)

借用參考3中部落格解析

把(4)(6)(7)式帶入到(3)式中去，並進行化簡

其中\eta =K_{11}+K_{22}-2K_{12}

得到\alpha _{2}^{new,unc}=\alpha _{2}^{old}+\frac{y_{2}(E_{1}-E_{2})}{\eta }…………(8)

 

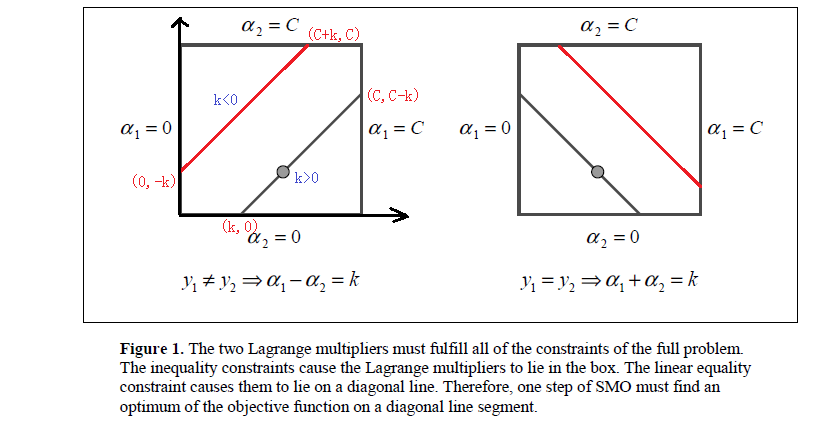
3、對原始解進行裁剪

裁剪的問題，部落格2裡得部分講的很詳細(具體的就不貼出來，請參看最後的參考博文連結)

對約束條件對應的*式\alpha _{1}y_{1}+\alpha _{2}y_{2}=\xi，考慮兩種情況，分別如上圖所示。

\alpha _{2}^{new}需要滿足約束條件0\leq \alpha _{i}\leq C，所以最優值\alpha _{2}^{new}的取值範圍也要滿足條件L\leqslant \alpha _{2}^{new}\leqslant H

L和H分別是\alpha _{2}^{new}坐在的對角線段端點的界。

 

當y_{1}\neq y_{2}時，\alpha _{2}的可行域為\left [max(0,\alpha _{1}-\alpha _{2}), \right min(C,C-\alpha _{1}+\alpha _{2})]，區間端點分別為：

L=max(0,\alpha _{2}^{old}-\alpha _{1}^{old})，H=min(C,C+\alpha _{2}^{old}-\alpha _{1}^{old})

當y_{1}= y_{2}時，\alpha _{2}的可行域為\left [max(0,\alpha _{1}+\alpha _{2}-C), \right min(C,\alpha _{1}+\alpha _{2})]，區間端點分別為：

L=max(0,\alpha _{2}^{old}+\alpha _{1}^{old}-C)，H=min(C,\alpha _{2}^{old}+\alpha _{1}^{old})

所以在更新\alpha _{2}時，要先求出\alpha _{2}的可行域，然後用之前的那個公式求出極值點\alpha _{2}，然後看極值點\alpha _{2}處的在不在可行域範圍內，在的話就使用極值點處的\alpha _{2}，不在的話就使用邊界值H或者L更新，具體更新規則為：

 

4、求解\alpha _{1}^{new}

由於只有兩個變數，根據\alpha _{1}^{old}y_{1}+\alpha _{2}^{old}y_{2}=\alpha _{1}^{new}y_{1}+\alpha _{2}^{new}y_{2}

可以求得\alpha _{1}^{new}=\alpha _{1}^{old}+y_{1}y_{2}(\alpha _{2}^{new}-\alpha _{2}^{new})…………(9)

 

其他一些內容涉及到論文《Sequential Minimal Optimization A Fast Algorithm for Training Support Vector Machines》

等看完再補充

 

選擇變數的啟發式方法

1、第1個變數的選擇

SMO稱第1個變數的選擇稱為外迴圈。外迴圈在訓練樣本中選取違反KKT條件最嚴重的樣本點，將其作為第一個變數。

遍歷的時候首先遍歷滿足0\leq \alpha _{i}\leq C的樣本點，也就是在間隔邊界上的支援向量點，檢驗是否滿足KKT條件；

如果都滿足，那麼遍歷整個訓練集，檢驗是否滿足KKT條件。

 

2、第2個變數的選擇

SMO稱第2個變數的選擇稱為內迴圈。在找到第一個變數的基礎上，第二個變數的標準是希望能使\alpha _{2}有足夠大的變化。

由上述的(8)式，\alpha _{2}是依賴於|E1−E2|，為了加快計算的速度，做簡單的就是選擇|E1−E2|最大時的\alpha _{2}

當E1為正時，那麼選擇最小的Ei作為E2；如果E1為負，選擇最大Ei作為E2。

為了節省時間，通常為每個樣本的Ei儲存在一個列表中，選擇最大的|E1−E2|來近似最大化步長。 

 

3、計算閾值b和差值E_{i}

這一部分還沒理解。空著先……

 

 

參考：

1、李航的《統計學習方法》

2、第三部分：SMO演算法的個人理解

3、【機器學習詳解】SMO演算法剖析

相關推薦

SMO演算法理解

SMO演算法看了近3遍感覺還是有點朦朦朧朧，模模糊糊。 所以索性，理解多少寫多少，避免遺忘。可能會有很多錯誤，歡迎指正。 主要基於李航的《統計學習方法》 SMO(sequential minimal optimization)序列最小最優化演算法 我們在討論支援向量機的學習問

深入理解SVM，詳解SMO演算法

今天是**機器學習專題**第35篇文章，我們繼續SVM模型的原理，今天我們來講解的是SMO演算法。 ## 公式回顧 在之前的文章當中我們對硬間隔以及軟間隔問題都進行了分析和公式推導，我們發現軟間隔和硬間隔的形式非常接近，只有少數幾個引數不同。所以我們著重來看看軟間隔的處理。 通過拉格朗日乘子

目標檢測演算法理解：從R-CNN到Mask R-CNN

　　因為工作了以後時間比較瑣碎，所以更多的時候使用onenote記錄知識點，但是對於一些演算法層面的東西，個人的理解畢竟是有侷限的。我一直做的都是影象分類方向，最近開始接觸了目標檢測，也看了一些大牛的論文，雖然網上已經有很多相關的演算法講解，但是每個人對同一個問題的理解都不太一樣，本文主

Candy演算法--理解

Canny邊緣檢測運算元的目標是找到一個最優的邊緣檢測演算法，最優邊緣檢測的含義是： 好的檢測 - 演算法能夠儘可能多地標識出影象中的實際邊緣。 好的定位 - 標識出的邊緣要與實際影象中的實際邊緣儘可能接近(邊緣過粗，難以精確定位)。 最小響應 -

hashcode和equals及雜湊演算法理解

因為會設計到很多equal的知識，所以先深入理解一下equals(). 1.equals（） Object類中的預設equals()方法和==是沒有區別的，都是判斷兩個物件是否指向同一個引用，記憶體地址是否相同，即是否就是一個物件。而string類和integer等，都需要重寫equals（）方

ALS演算法理解和引數調優

在上一篇博文中我們一起學習瞭如何用spark構建一套歌手推薦系統，在模型訓練的時候，我們用到的是ALS演算法，這篇博文我們就一起來學習一下ALS演算法的原理吧。ALS演算法全稱是Alternating Least Squares，從協同過濾的分類來說，這裡的ALS演算法是同時基於使用者和

ML之SVM：利用Js語言設計SVM演算法(SMO演算法+線性核/高斯核)

ML之SVM：利用Js語言設計SVM演算法(SMO演算法+線性核/高斯核) 輸出結果   設計思路     設計程式碼(部分程式碼) var doTest = function() { loadData();

SMO演算法daidingdaiding

SMO演算法：Sequential Minimal Optimization序列最小優化。把所有整個的二次規劃的求解問題，轉換成一系列的只含每一次只含兩個訓練樣本的α優化問題，是因為st約束條件中對α的限制。每次拿出兩個α來計算求解。 SMO基本思想：通過觀察SVM的優化目標，可以發現其最終

SVM SMO演算法程式碼詳細剖析

演算法實現 一：本文要結合SVM理論部分來看即筆者另一篇https://blog.csdn.net/weixin_42001089/article/details/83276714 二：有了理論部分下面就是直接程式碼啦，本文用四部分進行介紹：最簡版的SMO，改進版platt SMO，核函式，

PHP中選擇排序的演算法理解

選擇排序，原理： 在每一次大迴圈的時候得出一個最大值或者最小值來替換相應的位置，看程式碼： <?php $arr = [3,2,4,7,5]; for($i=0;$i<count($arr);$i++){      //第一次迴圈假設第一個元

貪心演算法理解

貪心演算法 基本思想： 貪心演算法通過一系列的選擇來得到問題的解，其中每一個選擇都是當前狀態下區域性最好的選擇，即貪心選擇 它有兩個重要性質：貪心選擇性質和最優子結構性質。 貪心選擇性質：指問題的最優解可以通過一系列區域性最優解的選擇得到。貪心演算法做貪心選擇可 以依賴於以往所做過的選擇，但決不依賴

【轉載】Folyd演算法理解

一篇非常優秀的解析 傳送門 floyd演算法:我們真的明白floyd嗎? 2016年08月02日 20:14:18 ljhandlwt 閱讀數：7444 標籤： floyd 演算法 更多 個人分類： 演算法  

斯坦福CS229機器學習筆記-Lecture8- SVM支援向量機 之核方法 + 軟間隔 + SMO 演算法

作者：teeyohuang 本文系原創，供交流學習使用，轉載請註明出處，謝謝 宣告：此係列博文根據斯坦福CS229課程，吳恩達主講 所寫，為本人自學筆記，寫成部落格分享出來           博文中部分圖片和公式都來源於CS229官方notes。      

粒子群演算法理解+求解01揹包問題

最近在學群體優化演算法，做個學習筆記吧，本人蒟蒻，有不對的地方還情多多包涵。 1.粒子群演算法的理解。         粒子群演算法是一種智慧優化演算法，模擬的是鳥內捕食行為。假設有一群鳥，在一個區域內覓食，這個區域內只有一個食物（最優解），但是每個鳥只知道自己距食物的距

網路請求中常見的加密機制和加密演算法理解

請求安全性： 伺服器端在接收到請求的時候，要主動鑑別該請求是否有效，是否可接受。 　　token:已登陸使用者的識別碼 　　　　解決的問題:使用者呼叫介面時，不用每次都帶上使用者名稱和密碼，避免了頻繁在網路中傳輸密碼被截獲的風險。 　　　　使用場景:使用者登入系統時傳入使用者名稱和密碼，伺服器校驗成功之後，根

SSD演算法理解（2）

作者：葉 虎 編輯：祝鑫泉 前言 目標檢測近年來已經取得了很重要的進展，主流的演算法主要分為兩個型別：（1）two-stage方法，如R-CNN系演算法，其主要思路是先通過啟發式方法（selective search）或

gcForest演算法理解

一、相關理論 本篇博文主要介紹南京大學周志華教授在2017年提出的一種深度森林結構——gcForest（多粒度級聯森林）。近年來，深度神經網路在影象和聲音處理領域取得了很大的進展。關於深度神經網路，我們可以把它簡單的理解為多層非線性函式的堆疊，當我們人工很難或者不想去尋找兩個目標之間的非線性

回溯演算法理解

一、演算法含義 回溯演算法也叫試探法，它是一種系統地搜尋問題的解的方法。回溯演算法的基本思路是：暴力演算法的改進，在通過遍歷所有路徑基礎上，通過回溯（往回找）篩除不可能的路徑，提高效率。 二、解題步驟： 1.確定一個解空間，它包含問題的解；2.利用適於搜尋的方法組織解空間；3.利用深度優先法搜尋解空間；

資料結構篇：校園最短路徑導航（二：弗洛伊德演算法理解與應用）

求最短路徑最常用的有迪傑斯特拉（Dijkstra）和弗洛伊德（Floyd）演算法兩種。本著簡潔為王道的信條，我選擇了Floyd演算法。 Floyd演算法 首先來看一個簡單圖，紅色標記代表在陣列的下標，橙色標記代表距離（邊權值） 我們用D[6][6]這個矩陣儲存兩點之間最短路徑，

JVM:GC-常用演算法理解

標記-清除 實現原理： 1、標記：標記出所有需要被回收的物件 2、清除：標記完成後，統一回收所有被標記的物件 圖示： 缺點： 1、效率：標記和清除的效率都不高 2、空間：標記清除後會有大量不連續的碎片空間存在，當分配一個大物件時，很有可能因為找不到足夠大的連續空間而導致第二次G