演算法實現

一：本文要結合SVM理論部分來看即筆者另一篇https://blog.csdn.net/weixin_42001089/article/details/83276714

二：有了理論部分下面就是直接程式碼啦，本文用四部分進行介紹：最簡版的SMO，改進版platt SMO，核函式，sklearn庫的SVM，四部分以%%%%%%%分開，採取的順序是先給程式碼及結果，然後分析

三：這裡程式碼大部分來自於Peter Harrington編寫的Machine Learning in Action

其網路資源https://www.manning.com/books/machine-learning-in-action

四：程式碼中需要注意的一點就是採用啟發式來尋找需要優化的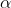 $\alpha$

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

首先看一下最簡版的smo優化演算法：

這裡有兩個py檔案，一個是用來構造SVM的，一個是用來測試的：

MySVM:

# -*- coding: utf-8 -*-
import random
import  numpy  as np
import matplotlib.pyplot as plt
#輔助函式一
def selectJrand(i, m):
    j = i  
    while (j == i):
        j = int(random.uniform(0, m))
    return j
#輔助函函式二
def clipAlpha(aj,H,L):
    if aj > H:
        aj = H
    if L > aj:
        aj = L
    return aj

#最簡版本SMO演算法
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
    dataMatrix = np.mat(dataMatIn); 
    labelMat = np.mat(classLabels).transpose()
    b = 0; 
    m,n = np.shape(dataMatrix)
    alphas = np.mat(np.zeros((m,1)))
    iter_num = 0
    while (iter_num < maxIter):
        alphaPairsChanged = 0
        for i in range(m):
            #注意一
            fXi = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b
            Ei = fXi - float(labelMat[i])
            if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
                j = selectJrand(i,m)
                fXj = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b
                Ej = fXj - float(labelMat[j])
                alphaIold = alphas[i].copy();
                alphaJold = alphas[j].copy();
                if (labelMat[i] != labelMat[j]):
                    L = max(0, alphas[j] - alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])
                if L==H: 
                    print("L==H"); 
                    continue
                #注意二
                eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
                if eta >= 0: 
                    print("eta>=0"); 
                    continue
                
                alphas[j] -= labelMat[j]*(Ei - Ej)/eta
              
                alphas[j] = clipAlpha(alphas[j],H,L)
               
                if (abs(alphas[j] - alphaJold) < 0.00001): print("alpha_j變化小，不需要更新"); continue
                #注意三
                alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])

                #注意四
                b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
                b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
             
                if (0 < alphas[i]) and (C > alphas[i]): b = b1
                elif (0 < alphas[j]) and (C > alphas[j]): b = b2
                else: b = (b1 + b2)/2.0
               
                alphaPairsChanged += 1
              
                print("第%d次迭代 樣本:%d, alpha優化次數:%d" % (iter_num,i,alphaPairsChanged))
       
        if (alphaPairsChanged == 0): 
            iter_num += 1
        else: iter_num = 0
        print("迭代次數: %d" % iter_num)
    #注意五
    return b,alphas
def calcWs(dataMat, labelMat, alphas):
    alphas, dataMat, labelMat = np.array(alphas), np.array(dataMat), np.array(labelMat)
    w = np.dot((np.tile(labelMat.reshape(1, -1).T, (1, 2)) * dataMat).T, alphas)
    return w.tolist()

def showClassifer(dataMat,labelMat,alphas, w, b):
    data_plus = []                                  
    data_minus = []
    #注意六
    for i in range(len(dataMat)):
        if labelMat[i] > 0:
            data_plus.append(dataMat[i])
        else:
            data_minus.append(dataMat[i])
    data_plus_np = np.array(data_plus)              
    data_minus_np = np.array(data_minus)            
    plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1], s=30, alpha=0.7)   
    plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1], s=30, alpha=0.7) 
    #注意七
    x1 = max(dataMat)[0]
    x2 = min(dataMat)[0]
    a1, a2 = w
    b = float(b)
    a1 = float(a1[0])
    a2 = float(a2[0])
    y1, y2 = (-b- a1*x1)/a2, (-b - a1*x2)/a2
    plt.plot([x1, x2], [y1, y2])
    #注意八
    for i, alpha in enumerate(alphas):
        if 0.6>abs(alpha) > 0:
            x, y = dataMat[i]
            plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='red')
        if 0.6==abs(alpha) :
            x, y = dataMat[i]
            plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='yellow')
    plt.show()

接著是測試函式（MyTest）：

# -*- coding: utf-8 -*-#
import MySVM as svm
x=[[1,8],[3,20],[1,15],[3,35],[5,35],[4,40],[7,80],[6,49],[1.5,25],[3.5,45],[4.5,50],[6.5,15],[5.5,20],[5.8,74],[2.5,5]]
y=[1,1,-1,-1,1,-1,-1,1,-1,-1,-1,1,1,-1,1]
b,alphas = svm.smoSimple(x,y,0.6,0.001,40)
w = svm.calcWs(x,y,alphas)
svm.showClassifer(x,y,alphas, w, b)

執行結果：

，，，，，，，，，，，，，

接下來一步步分析MySVM中的程式碼

首次看兩個簡單的輔助函式，第一個函式的作用就是用來選擇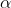 $\alpha$ 對的（即尋找i，j這一對）

第二個函式就是為了將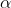 $\alpha$ 規劃到[0,C]範圍內，對應到理論推導部分的：

$\alpha ^{*}_{2}=\begin{Bmatrix} L\, \,\, \, \, \, \, \, \, \, \, \, if \, \, \, \,\alpha _{2}<L\\ \alpha _{2}\, \,\, \, \, \, \, \, \, \, if \, \, \, L\leq \alpha _{2}\leqslant H\\ H\,\, \, \, \, \, \, \, \, \, \, \, if \, \, \alpha _{2}> H \end{Bmatrix}$

接下來就是smo演算法的最簡版本：

注意一下面的fXi對應推導公式的即w的更新：

$w=\sum_{i=1}^{m}\alpha _{i}y_{i}x_{i}\, \, \, \, (9)$

可能這裡和上篇最後給出w的更新形式上看上去有點不對應，其實是一樣的，推導部分即最後一張圖是：

$w = w+y_{1}(\alpha_{1} ^{*}-\alpha_{1} )x_{1}+y_{2}(\alpha_{2} ^{*}-\alpha_{2} )x_{2}$

而這裡的其實在程式就是對應的就是如下三步：

 fXi = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b

 alphas[j] -= labelMat[j]*(Ei - Ej)/eta
 alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])

緊接著的if這裡就是啟發式選擇，即尋找那些誤差過大（正間隔和否間隔）且在（0，C）範圍內的 $\alpha$ 進行優化，選擇誤差大的進行優化我們很容易理解，那為什麼要選擇（0，C）範圍內，而不選擇邊界值呢（值等於0或C），那是因為它們已經在邊界啦，因此不再能夠減少或者增大具體細節請看推導部分，該部分包括L和H為什麼要這樣賦值，以及為什麼L==H的時候要返回都有講到。

注意二的部分就是類似我們在推導部分的 $\alpha _{2}$ 更新，只不過這裡有一步如果變化太小我們就不更新了，直接跳過，只不過原公式中的 $\theta =-eta$ ，所以推導中原本 $\alpha _{2}$ 是加上後面的，而這裡是減即：本質是一樣的啦，當然 $\alpha _{1}$ 更新方向要相反，所以程式碼中對應的是+

 alphas[j] -= labelMat[j]*(Ei - Ej)/eta

至於為什麼eta >= 0為什麼要跳過該次迴圈，請看推導部分，只不過因為 $\theta =-eta$ 所以原來是過濾掉<=0,這裡是>=0

注意三部分就是類似 $\alpha _{1}$ 的更新即大小和 $\alpha _{2}$ 相同，方向相反

注意四的部分應該很直觀啦，看我們推導的b的更新結論一目瞭然

注意五返回的b是一個實數，alphas是一個[m,1]矩陣

最後說一下smo函式的alphaPairsChanged和iter_num以及maxIter的引數意義，maxIter是最外部的大迴圈，是人為設定的最大迴圈次數，迴圈為最大次數後就強行結束返回，在每一個大迴圈下都有一個for迴圈，用以遍歷一遍所有的 $\alpha$ ，遍歷完這一遍所有的 $\alpha$ 後，alphaPairsChange用以記錄看有多少對被優化啦，如果alphaPairsChange不為0，即這一遍走下來後，我們進行了優化，也就代表目前 $\alpha$ 還不夠好，所以我們將iter_num設為0，繼續優化，當alphaPairsChange為0時，說明我們這一遍走下來，說明 $\alpha$ 都很好啦，沒有優化的必要啦，我們將iter_num加一，接著下一遍再去整體看看 $\alpha$ ，如果還是alphaPairsChange為0，恩恩，不錯，不錯，將iter_num再加一，如果iter_num到了maxIter即連續進行了maxIter遍整體（for）觀察都沒發現需要優化的 $\alpha$ ，說明足夠好了，返回吧！！！！！！一旦中間出現意外，發現有需要優化的，就至少說明有不完善的地方，那麼我們立馬讓iter_num為0，即一定要達到連續遍歷maxIter次都沒發現不足，我們才放心，才返回，發現瑕疵立馬iter_num=0從頭開始，怎麼樣？就是這麼嚴格，這也是上面執行結果開始的時候為什麼迭代次數一直都是0，後面趨於收斂，迭代次數連續增加，直到maxIter結束返回

正是因為如此，可以想象得的到帶來的結果就是時間複雜度太高，所以有了後來改進版本的Platt SMO，後面介紹

接下來的calcWs函式作用是:根據訓練出來的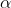 $\alpha$ 生成w：

對應的公式就是：

$w=\sum_{i=1}^{m}\alpha _{i}y_{i}x_{i}\, \, \, \, (9)$

目前我們已經訓練除了SVM模型，即得到了我們想要的w和b，對應的步驟就在上面所說的黃色部分

接下來視覺化看一下結果showClassifer：

注意六的部分就是我們把原始點畫出來，不同的顏色代表不同的分離（橙色的點對應的標籤是-1，藍色的點對應的標籤是1）

注意七的部分就是畫出訓練出來的超平面

y1, y2 = (-b- a1*x1)/a2, (-b - a1*x2)/a2

這個很好理解啦，超平面是：

$0=x_{1}w_{1}+x_{2}w_{2}+b$

所以：

$x_{2}=\frac{-x_{1}w_{1}-b}{w_{2}}$

程式中為了讓超平面儘可能的橫穿整個資料點，所以選取了所有點中x座標最大和最小的點即x1和x2：

然後利用上面的公式，計算出了對應的縱座標

注意八的部分就是畫出向量機點，和那些我們“忽略”的點，依據是推導的：

$\begin{matrix} \alpha _{i}=0\Leftrightarrow y_{i}y(x)\geq 1\\ 0< \alpha _{i}< C\Leftrightarrow y_{i}y(x)= 1 \\ \alpha _{i}=C\Leftrightarrow y_{i}y(x)\leq 1 \end{matrix}$

即在點在兩條間隔線外則，對應前面的係數 $\alpha$ 為0，在兩條間隔線裡面的對應的係數為C，在兩條間隔線上的點對應的係數在0和C之間。至於為什麼請看上篇的推導細節

帶有紅色圓圈的是支援向量機點即間隔線上的點，帶有黃色的點是間隔線內的點

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Platt SMO：

其是SMO演算法的一個改進版，速度更快。

其主要變化的地方有兩個

一：在使用啟發式方法選擇了一個 $\alpha$ 後，我們會去選擇另外一個與之對應是吧，即

 j = selectJrand(i,m)

但是改進的的SMO演算法中，這裡也使用啟發式來選擇，即選擇與Ei誤差最大的Ej即選擇最大步長，簡單來說就是找最需要優化的j,而不是像最簡版本那樣，毫無目的的隨機去選擇，所以對應到推導公式裡面就是 $\alpha _{1}$ 和 $\alpha _{2}$ 都採用啟發式來尋找

二：改進後的演算法是採用在“非邊界值”和“邊界值”範圍內交替遍歷優化的

下面來看一下具體程式碼：

smoP：

# -*- coding: utf-8 -*-
from numpy import *
import matplotlib.pyplot as plt
import random
def loadDataSet(filename): 
    dataMat=[]
    labelMat=[]
    fr=open(filename)
    for line in fr.readlines():
        lineArr=line.strip().split('\t')
        dataMat.append([float(lineArr[0]),float(lineArr[1])])
        labelMat.append(float(lineArr[2]))
    return dataMat,labelMat 
class optStruct:
    def __init__(self,dataMatIn, classLabels, C, toler, kTup):  
        self.X = dataMatIn  
        self.labelMat = classLabels 
        self.C = C 
        self.tol = toler 
        self.m = shape(dataMatIn)[0] 
        self.alphas = mat(zeros((self.m,1)))
        self.b = 0 
        self.eCache = mat(zeros((self.m,2)))
def selectJrand(i,m): 
    j=i
    while (j==i):
        j=int(random.uniform(0,m))
    return j

def clipAlpha(aj,H,L):  
    if aj>H:
        aj=H
    if L>aj:
        aj=L
    return aj
        
def calcEk(oS, k): 
    fXk = float(multiply(oS.alphas,oS.labelMat).T*(oS.X*oS.X[k,:].T) + oS.b)
    Ek = fXk - float(oS.labelMat[k])
    return Ek

def selectJ(i, oS, Ei):
    maxK = -1
    maxDeltaE = 0
    Ej = 0
    oS.eCache[i] = [1,Ei]
    validEcacheList = nonzero(oS.eCache[:,0].A)[0]  
    if (len(validEcacheList)) > 1:
        for k in validEcacheList:
            if k == i:
                continue
            Ek = calcEk(oS, k)
            deltaE = abs(Ei - Ek)
            if (deltaE > maxDeltaE): 
                maxK = k
                maxDeltaE = deltaE
                Ej = Ek
        return maxK, Ej
    else:
        j = selectJrand(i, oS.m)
        Ej = calcEk(oS, j)
    return j, Ej
def updateEk(oS, k): 
    Ek = calcEk(oS, k)
    oS.eCache[k] = [1,Ek]

def innerL(i, oS):
    Ei = calcEk(oS, i) 
    if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)): 
        j,Ej = selectJ(i, oS, Ei)
        alphaIold = oS.alphas[i].copy()
        alphaJold = oS.alphas[j].copy()
        if (oS.labelMat[i] != oS.labelMat[j]): 
            L = max(0, oS.alphas[j] - oS.alphas[i])
            H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
        else:
            L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
            H = min(oS.C, oS.alphas[j] + oS.alphas[i])
        if L==H:
            print("L==H")
            return 0
        eta = 2.0 * oS.X[i,:]*oS.X[j,:].T-oS.X[i,:]*oS.X[i,:].T-oS.X[j,:]*oS.X[j,:].T
        if eta >= 0:
            print("eta>=0")
            return 0
        oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta 
        oS.alphas[j] = clipAlpha(oS.alphas[j],H,L) 
        updateEk(oS, j)
        if (abs(oS.alphas[j] - alphaJold) < oS.tol): 
            print("j not moving enough")
            return 0
        oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])
        updateEk(oS, i) 
        b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[i,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[i,:]*oS.X[j,:].T
        b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[j,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[j,:]*oS.X[j,:].T
        if (0 < oS.alphas[i]<oS.C):
            oS.b = b1
        elif (0 < oS.alphas[j]<oS.C):
            oS.b = b2
        else:
            oS.b = (b1 + b2)/2.0
        return 1
    else:
        return 0

def calcWs(dataMat, labelMat, alphas):
    alphas, dataMat, labelMat = array(alphas), array(dataMat), array(labelMat)
    w = dot((tile(labelMat.reshape(1, -1).T, (1, 2)) * dataMat).T, alphas)
    return w.tolist()

def smoP(dataMatIn, classLabels, C, toler, maxIter,kTup=('lin', 0)): 
    oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler, kTup)
    iter = 0
    entireSet = True
    alphaPairsChanged = 0
    while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
        alphaPairsChanged = 0
        if entireSet:
            for i in range(oS.m):
                alphaPairsChanged += innerL(i,oS)
                print("fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged)) 
            iter += 1
        else:
            nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
            for i in nonBoundIs: 
                alphaPairsChanged += innerL(i,oS)
                print("non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
            iter += 1
        if entireSet:
            entireSet = False
        elif (alphaPairsChanged == 0):
            entireSet = True
        print("iteration number: %d" % iter)
    return oS.b,oS.alphas

def showClassifer(dataMat,labelMat,alphas, w, b):
    data_plus = []                                  
    data_minus = []
    for i in range(len(dataMat)):
        if labelMat[i] > 0:
            data_plus.append(dataMat[i])
        else:
            data_minus.append(dataMat[i])
    data_plus_np = array(data_plus)              
    data_minus_np = array(data_minus)            
    plt.scatter(transpose(data_plus_np)[0], transpose(data_plus_np)[1], s=30, alpha=0.7)   
    plt.scatter(transpose(data_minus_np)[0], transpose(data_minus_np)[1], s=30, alpha=0.7) 
    x1 = max(dataMat)[0]
    x2 = min(dataMat)[0]
    a1, a2 = w
    b = float(b)
    a1 = float(a1[0])
    a2 = float(a2[0])
    y1, y2 = (-b- a1*x1)/a2, (-b - a1*x2)/a2
    plt.plot([x1, x2], [y1, y2])
    for i, alpha in enumerate(alphas):
        if 0.6>abs(alpha) > 0:
            x, y = dataMat[i]
            plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='red')
        if 50==abs(alpha) :
            x, y = dataMat[i]
            plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='yellow')
    plt.show()

接著還是測試函式（MyTest）：

# -*- coding: utf-8 -*-#
import smoP as svm
x=[[1,8],[3,20],[1,15],[3,35],[5,35],[4,40],[7,80],[6,49],[1.5,25],[3.5,45],[4.5,50],[6.5,15],[5.5,20],[5.8,74],[2.5,5]]
y=[1,1,-1,-1,1,-1,-1,1,-1,-1,-1,1,1,-1,1]
b,alphas = svm.smoP(x,y,50,0.001,40)
w = svm.calcWs(x,y,alphas)
svm.showClassifer(x,y,alphas, w, b)

，，，，，，，，，，，

這裡首先optStruct函式定義了一個類作為資料結構來儲存一些資訊，這裡面的alphas就是我們的 $\alpha$ ，eCache第一列就是一個是否有效的標誌位，第二列儲存著誤差值E，總之這個結構體的定義就是為了作為一個整體，方便呼叫，管理。

calcEk和最簡版本沒什麼差別，只不過我們已經定義了結構體，所以直接可以呼叫結構體便可得到一些資訊，所以下面所有程式碼都是這樣，比如C我們可以直接用oS.C等等

selectJ和最簡版本不一樣啦，這裡也就是我們說的用啟發式來尋找j,這裡的：

if (len(validEcacheList)) > 1:

主要是防止第一次迴圈的時候，如果是第一次那麼就隨機選擇，之後都使用啟發式來選擇

updateEk就是用來在計算完i和j的Ei和Ej後更新資料結構中的的eCache

innerL和最簡版本的smoSimple內迴圈（就是for迴圈下面的程式碼：用來優化 $\alpha$ 和b的核心程式碼）一模一樣，只不過這裡要把一些東西，改為資料結構中定義的，而且這裡的selectJ已經採用了啟發式尋找

接下來就是我們的smoP，也是Platt SMO利用主迴圈封裝整個演算法的過程，其和最簡版本一樣，也是兩個迴圈：

外訓練也是使用了一個maxIter，同時使用了iter來記錄遍歷次數（對應最簡版本的iter_num）,但是兩者含義卻不一樣，這裡的iter就是單純的代表一次迴圈，而不管迴圈內部具體做了什麼，它沒有被清0這個過程，隨著程式執行一直是個累加的過程，上面執行結果也可以看到iter是一直遞增的，這也是Platt SMO之所以能夠加快演算法的一個重要原因，而最簡版本的iter_num要肩負著連續這一條件，同時這裡的外迴圈相對於最簡版本的的外迴圈多了一個退出條件即：遍歷整個集合都沒發現需要改變的 $\alpha$ （說明都優化好啦，退出吧）

再來看一下內迴圈，這裡對應著兩種情況，一種是在全集上面遍歷（[0,C]），另一種是非邊界上面（（0，C）），通過

if entireSet:
            entireSet = False
        elif (alphaPairsChanged == 0):
            entireSet = True

使兩種情況交替遍歷

其他部分包括W的獲得，視覺化什麼的就和最簡版本一樣啦，不再重複介紹啦

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

核函式

核函式的作用細節請看推導部分，核函式種類很多，這裡看一下最常用的徑向基高斯（RBF）核函式

下面來簡單說一下部分程式碼（這裡只說不同的地方，相同的地方不再重述）

# -*- coding: utf-8 -*-
from numpy import *
import matplotlib.pyplot as plt
def loadDataSet(filename): 
    dataMat=[]
    labelMat=[]
    fr=open(filename)
    for line in fr.readlines():
        lineArr=line.strip().split(',')
        dataMat.append([float(lineArr[0]),float(lineArr[1])])
        labelMat.append(float(lineArr[2]))
    return dataMat,labelMat 

def selectJrand(i,m): 
    j=i
    while (j==i):
        j=int(random.uniform(0,m))
    return j

def clipAlpha(aj,H,L):  
    if aj>H:
        aj=H
    if L>aj:
        aj=L
    return aj

def kernelTrans(X, A, kTup): 
    m,n = shape(X)
    K = mat(zeros((m,1)))
    if kTup[0]=='lin': 
        K = X * A.T
    elif kTup[0]=='rbf': 
        for j in range(m):
            deltaRow = X[j,:] - A
            K[j] = deltaRow*deltaRow.T
        K = exp(K/(-1*kTup[1]**2)) 
    else:
        raise NameError('Houston We Have a Problem -- That Kernel is not recognized')
    return K


class optStruct:
    def __init__(self,dataMatIn, classLabels, C, toler, kTup):  
        self.X = dataMatIn  
        self.labelMat = classLabels 
        self.C = C 
        self.tol = toler 
        self.m = shape(dataMatIn)[0] 
        self.alphas = mat(zeros((self.m,1)))
        self.b = 0 
        self.eCache = mat(zeros((self.m,2))) 
        self.K = mat(zeros((self.m,self.m))) 
        for i in range(self.m):
            self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup)


def calcEk(oS, k):
    fXk = float(multiply(oS.alphas,oS.labelMat).T*oS.K[:,k] + oS.b)
    Ek = fXk - float(oS.labelMat[k])
    return Ek

def selectJ(i, oS, Ei):
    maxK = -1
    maxDeltaE = 0
    Ej = 0
    oS.eCache[i] = [1,Ei]
    validEcacheList = nonzero(oS.eCache[:,0].A)[0]  
    if (len(validEcacheList)) > 1:
        for k in validEcacheList:
            if k == i:
                continue
            Ek = calcEk(oS, k)
            deltaE = abs(Ei - Ek)
            if (deltaE > maxDeltaE): 
                maxK = k
                maxDeltaE = deltaE
                Ej = Ek
        return maxK, Ej
    else:
        j = selectJrand(i, oS.m)
        Ej = calcEk(oS, j)
    return j, Ej


def updateEk(oS, k): 
    Ek = calcEk(oS, k)
    oS.eCache[k] = [1,Ek]


def innerL(i, oS):
    Ei = calcEk(oS, i) 
    if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)): 
        j,Ej = selectJ(i, oS, Ei) 
        alphaIold = oS.alphas[i].copy()
        alphaJold = oS.alphas[j].copy()
        if (oS.labelMat[i] != oS.labelMat[j]):
            L = max(0, oS.alphas[j] - oS.alphas[i])
            H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
        else:
            L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
            H = min(oS.C, oS.alphas[j] + oS.alphas[i])
        if L==H:
            print("L==H")
            return 0
        eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j] 
        if eta >= 0:
            print("eta>=0")
            return 0
        oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta 
        oS.alphas[j] = clipAlpha(oS.alphas[j],H,L) 
        updateEk(oS, j)
        if (abs(oS.alphas[j] - alphaJold) < oS.tol): 
            print("j not moving enough")
            return 0
        oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])
        updateEk(oS, i) 
       
        b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]
        b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]
        if (0 < oS.alphas[i]<oS.C):
            oS.b = b1
        elif (0 < oS.alphas[j]<oS.C):
            oS.b = b2
        else:
            oS.b = (b1 + b2)/2.0
        return 1
    else:
        return 0


def smoP(dataMatIn, classLabels, C, toler, maxIter,kTup=('lin', 0)):
    oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler, kTup)
    iter = 0
    entireSet = True
    alphaPairsChanged = 0
    while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
        alphaPairsChanged = 0
        if entireSet:
            for i in range(oS.m): 
                alphaPairsChanged += innerL(i,oS)
                print("fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged)) 
            iter += 1
        else:
            nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
            for i in nonBoundIs: 
                alphaPairsChanged += innerL(i,oS)
                print("non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
            iter += 1
        if entireSet:
            entireSet = False
        elif (alphaPairsChanged == 0):
            entireSet = True
        print("iteration number: %d" % iter)
    return oS.b,oS.alphas


def testRbf(data_train,data_test):
    dataArr,labelArr = loadDataSet(data_train) 
    b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, ('rbf', 0.2)) 
    datMat=mat(dataArr)
    labelMat = mat(labelArr).transpose()
    svInd=nonzero(alphas)[0]  
    sVs=datMat[svInd] 
    labelSV = labelMat[svInd] 
    print("there are %d Support Vectors" % shape(sVs)[0]) 
    m,n = shape(datMat)
    errorCount = 0
    for i in range(m):
        kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', 1.3)) 
        predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b  
        if sign(predict)!=sign(labelArr[i]): 
            errorCount += 1
    print("the training error rate is: %f" % (float(errorCount)/m)) 
    dataArr_test,labelArr_test = loadDataSet(data_test) 
    errorCount_test = 0
    datMat_test=mat(dataArr_test)
    labelMat = mat(labelArr_test).transpose()
    m,n = shape(datMat_test)
    for i in range(m): 
        kernelEval = kernelTrans(sVs,datMat_test[i,:],('rbf', 0.1))
        predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
        if sign(predict)!=sign(labelArr_test[i]):
            errorCount_test += 1
    print("the test error rate is: %f" % (float(errorCount_test)/m))
    
    return dataArr,labelArr,alphas

def showClassifer(dataMat,labelMat,alphas):
    data_plus = []                                  
    data_minus = []
    for i in range(len(dataMat)):
        if labelMat[i] > 0:
            data_plus.append(dataMat[i])
        else:
            data_minus.append(dataMat[i])
    data_plus_np = array(data_plus)              
    data_minus_np = array(data_minus)            
    plt.scatter(transpose(data_plus_np)[0], transpose(data_plus_np)[1], s=30, alpha=0.7)   
    plt.scatter(transpose(data_minus_np)[0], transpose(data_minus_np)[1], s=30, alpha=0.7) 
    for i, alpha in enumerate(alphas):
        if abs(alpha) > 0:
            x, y = dataMat[i]
            plt.scatter([x], [y], s=150, c='none', alpha=0.7, linewidth=1.5, edgecolor='red')
    plt.show()

MyTest:

# -*- coding: utf-8 -*-
import smoPrbf as svm
traindata='C:\\Users\\asus-\\Desktop\\train_data.csv'
testdata='C:\\Users\\asus-\\Desktop\\test_data.csv'
TraindataArr,TrainlabelArr,alphas = svm.testRbf(traindata,testdata)
svm.showClassifer(TraindataArr,TrainlabelArr,alphas)

當 $\delta =0.2$ 時：

當 $\delta =1.2$ 時：

kernelTrans函式的作用就是核函式的計算部分，對應到推導公式是：

$K(x_{i},x)=exp(-\frac{\left \| x_{i}-x \right \|^{2}}{2\delta ^{2}})$

這裡的kTup就是指定使用什麼核函式，kTup[0]引數是核函式型別，kTup[1]是核函式需要的超引數，注意這裡只支援線性和徑向基高斯（RBF）核函式兩種.

optStruct函式增加了一個欄位即K，其是一個m*m的矩陣。注意它的含義：

我們的核函式是 $K(x_{i},x)$ 即拿來一個點x，要和所有樣本 $x_{i}$ 做運算，這裡的行代表的意義就是所有樣本，列代表的是x所以這裡是：

elf.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup)

innerL變化的部分是：

eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j]

對比之前的：

 eta = 2.0 * oS.X[i,:]*oS.X[j,:].T-oS.X[i,:]*oS.X[i,:].T-oS.X[j,:]*oS.X[j,:].T

就可以更好的理解為什麼在optStruct結構體中K欄位要這麼設計

同理變化的地方還有：

 b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]
 b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]

calcEk變化的地方：

fXk = float(multiply(oS.alphas,oS.labelMat).T*oS.K[:,k] + oS.b)

簡單來說就是原先有 $x_{i}x$ 的地方都要換成核函式的內積形式即 $x_{i}x\Rightarrow <x_{i},x>$

testRbf這裡主要作用就是使用了訓練集去訓練SVM模型，然後分別統計該模型在訓練集上和測試集上的錯誤率。

注意這裡在通過 $\alpha$ 構建權重w時是隻用到是支援向量機那些點即 $\alpha > 0$ 那些點，其實SVM的原理不就是使用這些向量機來構建的模型的嘛，那些遠離間隔線的點我們是用不到的，對我們沒什麼作用。所以先篩選出哪些點是向量機：

 svInd=nonzero(alphas)[0]

程式也會將向量機的個數打印出來。

最後討論一下rbf的超引數意義即 $\delta$ 值對應在在程式碼的：

b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, ('rbf', 0.2))

或

b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, ('rbf', 1.2))

通過上面的實驗我們可以大體看出隨著 $\delta$ 的增加，支援向量機的個數在減少，由原來的43個減少到25（紅色圓圈的點就是支援向量機）， $\delta$ 的取值存在一個最優解，當 $\delta$ 太大，支援向量機太少，也就是說我們利用了很少的點去決策，顯然結果不好，正如上面體現的那樣，測試集的錯誤在上升，當 $\delta$ 太小，支援向量機太多，也就是我們基本利用了所有樣本點，其實這個時候已經退化到類似KNN啦，因為KNN就是利用了到所有樣本點的距離來決策的，可能會有這樣的疑問？不對呀？使用KNN時不是會指定利用多少個點嗎？不是利用所有點呀？哈哈哈，仔細想想，它的過程是先計算到全部樣本的距離，然後再從中選擇K個最近距離的點來進行比較的，所以它每次要用到的是全部樣本點，而SVM是一旦訓練出 $\alpha$ 後，在之後的決策中就只使用 $\alpha > 0$ 的樣本，即使用部分點，這回明白了吧，再者SVM本質也是和KNN一樣使用距離來決策的，所以才說當支援向量機太多的時候，我們不就是使用全部樣本點通過計算距離來決策的嘛，這和KNN特別相似，當然啦，說了半天這也不是什麼重要的事情，只是為了增加SVM

的理解，最重要的還是要通過除錯找到RBF最佳的超引數值。

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

最後寫一個簡單的呼叫sklearn庫的SVM程式：

關於更多sklearn的SVM更多呼叫請看：

https://blog.csdn.net/weixin_42001089/article/details/79952399

當然還有其他機器學習的呼叫

# -*- coding: utf-8 -*-
from numpy import *
import matplotlib.pyplot as plt
from sklearn import metrics
from sklearn import svm

def loadDataSet(filename): 
    dataMat=[]
    labelMat=[]
    fr=open(filename)
    for line in fr.readlines():
        lineArr=line.strip().split(',')
        dataMat.append([float(lineArr[0]),float(lineArr[1])])
        labelMat.append(float(lineArr[2]))
    return dataMat,labelMat


traindata='C:\\Users\\asus-\\Desktop\\train_data.csv'
testdata='C:\\Users\\asus-\\Desktop\\test_data.csv'


x_train,y_train = loadDataSet(traindata)
x_test,y_test = loadDataSet(testdata)


clf1 = svm.SVC(C=0.8, kernel='rbf', gamma=10, decision_function_shape='ovr')
clf2 = svm.SVC(C=0.8, kernel='rbf', gamma=20, decision_function_shape='ovr')

clf1.fit(x_train, y_train)
clf2.fit(x_train, y_train)



y_predict1=clf1.predict(x_test)
y_predict2=clf2.predict(x_test)
print('--------------------- gamma=10--------------------------------')
print(metrics.classification_report(y_test,y_predict1))
print('--------------------- gamma=20--------------------------------')
print(metrics.classification_report(y_test,y_predict2))

結尾給一下我們用的資料集，方便大家實驗：

Train_data:

-0.214824	0.662756	-1
-0.061569	-0.091875	1
0.406933	0.648055	-1
0.22365	0.130142	1
0.231317	0.766906	-1
-0.7488	-0.531637	-1
-0.557789	0.375797	-1
0.207123	-0.019463	1
0.286462	0.71947	-1
0.1953	-0.179039	1
-0.152696	-0.15303	1
0.384471	0.653336	-1
-0.11728	-0.153217	1
-0.238076	0.000583	1
-0.413576	0.145681	1
0.490767	-0.680029	-1
0.199894	-0.199381	1
-0.356048	0.53796	-1
-0.392868	-0.125261	1
0.353588	-0.070617	1
0.020984	0.92572	-1
-0.475167	-0.346247	-1
0.074952	0.042783	1
0.394164	-0.058217	1
0.663418	0.436525	-1
0.402158	0.577744	-1
-0.449349	-0.038074	1
0.61908	-0.088188	-1
0.268066	-0.071621	1
-0.015165	0.359326	1
0.539368	-0.374972	-1
-0.319153	0.629673	-1
0.694424	0.64118	-1
0.079522	0.193198	1
0.253289	-0.285861	1
-0.035558	-0.010086	1
-0.403483	0.474466	-1
-0.034312	0.995685	-1
-0.590657	0.438051	-1
-0.098871	-0.023953	1
-0.250001	0.141621	1
-0.012998	0.525985	-1
0.153738	0.491531	-1
0.388215	-0.656567	-1
0.049008	0.013499	1
0.068286	0.392741	1
0.7478	-0.06663	-1
0.004621	-0.042932	1
-0.7016	0.190983	-1
0.055413	-0.02438	1
0.035398	-0.333682	1
0.211795	0.024689	1
-0.045677	0.172907	1
0.595222	0.20957	-1
0.229465	0.250409	1
-0.089293	0.068198	1
0.3843	-0.17657	1
0.834912	-0.110321	-1
-0.307768	0.503038	-1
-0.777063	-0.348066	-1
0.01739	0.152441	1
-0.293382	-0.139778	1
-0.203272	0.286855	1
0.957812	-0.152444	-1
0.004609	-0.070617	1
-0.755431	0.096711	-1
-0.526487	0.547282	-1
-0.246873	0.833713	-1
0.185639	-0.066162	1
0.851934	0.456603	-1
-0.827912	0.117122	-1
0.233512	-0.106274	1
0.583671	-0.709033	-1
-0.487023	0.62514	-1
-0.448939	0.176725	1
0.155907	-0.166371	1
0.334204	0.381237	-1 相關推薦 SVM SMO演算法程式碼詳細剖析演算法實現一：本文要結合SVM理論部分來看即筆者另一篇https://blog.csdn.net/weixin_42001089/article/details/83276714 二：有了理論部分下面就是直接程式碼啦，本文用四部分進行介紹：最簡版的SMO，改進版platt SMO，核函式， SMO（Sequential minimal optimization）演算法的詳細實現過程 SMO演算法主要是為優化SVM（支援向量機）的求解而產生的，SVM的公式基本上都可以推到如下這步： m a ML之SVM：利用Js語言設計SVM演算法(SMO演算法+線性核/高斯核) ML之SVM：利用Js語言設計SVM演算法(SMO演算法+線性核/高斯核) 輸出結果設計思路設計程式碼(部分程式碼) var doTest = function() { loadData(); 斯坦福CS229機器學習筆記-Lecture8- SVM支援向量機之核方法 + 軟間隔 + SMO 演算法作者：teeyohuang 本文系原創，供交流學習使用，轉載請註明出處，謝謝宣告：此係列博文根據斯坦福CS229課程，吳恩達主講所寫，為本人自學筆記，寫成部落格分享出來博文中部分圖片和公式都來源於CS229官方notes。詳解SVM系列（六）：深入解析序列最小最優化SMO演算法一 SMO演算法是幹啥的首先要先搞明白一個基本的問題： SMO演算法是幹啥的？通過前面的介紹，我們現在掌握了線性不可分支援向量機。其形式為如下的凸二次規劃： m 資料探勘十大演算法——支援向量機SVM（四）：SMO演算法原理首先感謝“劉建平pinard”的淵博知識以及文中詳細準確的推導！！！支援向量機原理SVM系列文章共分為5部分：（一）線性支援向量機（二）線性支援向量機的軟間隔最大化模型（三）線性不可分支援向量機與核函式（四）SMO演算法原理（五）線性支援迴歸 SVM中的對偶問題、KKT條件以及對拉格朗日乘子求值得SMO演算法考慮以下優化問題目標函式是f(w)，下面是等式約束。通常解法是引入拉格朗日運算元，這裡使用來表示運算元，得到拉格朗日公式為 L是等式約束的個數。然後分別對w和求偏導， Mahout機器學習平臺之聚類演算法詳細剖析（含例項分析）第一部分：學習Mahout必須要知道的資料查詢技能：學會查官方幫助文件：解壓用於安裝檔案（mahout-distribution-0.6.tar.gz），找到如下位置，我將該檔案解壓到win7的G盤mahout資料夾下，路徑如下所示： G:\mahout\mahout 關於SVM中SMO演算法第一個向量選擇的問題在看李航編寫的《統計學習方法》一書中第128頁時，涉及到SMO演算法中第一個變數的選擇，然後作者指出選擇不滿足KKT條件的變數作為第一個變數，然後突然給出瞭如下三個KKT條件: αi=0⇔yig(xi)≥1(1) 0<αi<C⇔yig(xi)=1( SVM 採用smo演算法計算 python 本文采用smo演算法計算svm 程式有點問題，開始才用的libsvm的程式碼，準備將其java程式碼寫成python的，後面發現用libsvm的資料格式老是出問題。就參考了機器學習實戰的程式碼。程式有很多要優化的地方 1）核函式要完善，這裡只寫了線性核函式。但是整個程 SVM支援向量機-《機器學習實戰》SMO演算法Python實現（5）經過前幾篇文章的學習，SVM的優化目標，SMO演算法的基本實現步驟，模型對應引數的選擇，我們已經都有了一定的理解，結合《機器學習實戰》，動手實踐一個基本的SVM支援向量機，來完成一個簡單的二分類任務。建立模型之前，首先看一下我們的資料，然後再用支援向量機實現分類：【機器學習詳解】SMO演算法剖析 CSDN−勿在浮沙築高臺本文力求簡化SMO的演算法思想，畢竟自己理解有限，無奈還是要拿一堆公式推來推去，但是靜下心看完本篇並隨手推導，你會迎刃而解的。推薦參看SMO原文中的虛擬碼。 1.SMO概念上一篇部落格已經詳細介紹了SVM原理，為了方便求解，把原深入理解SVM，詳解SMO演算法今天是機器學習專題第35篇文章，我們繼續SVM模型的原理，今天我們來講解的是SMO演算法。 ## 公式回顧在之前的文章當中我們對硬間隔以及軟間隔問題都進行了分析和公式推導，我們發現軟間隔和硬間隔的形式非常接近，只有少數幾個引數不同。所以我們著重來看看軟間隔的處理。通過拉格朗日乘子 mysql5.7：mysql安裝和基於SSL加密的主從復制（詳細剖析） mysql ssl db 數據加密傳輸小生博客：http://xsboke.blog.51cto.com 小生 Q Q：1770058260 -------謝謝您的參考，如有疑問，歡迎交流目錄：--------my Kylin官方案例詳細剖析及剪枝優化-OLAP商業環境實戰版權宣告：本套技術專欄是作者（秦凱新）平時工作的總結和昇華，通過從真實商業環境抽取案例進行總結和分享，並給出商業應用的調優建議和叢集環境容量規劃等內容，請持續關注本套部落格。版權宣告：禁止轉載，歡迎學習。 Kylin官方案例是一個非常經典的案例，包含的技術細節通過深挖能呈現出更具價值的資訊，如：資料倉庫理論數獨問題的一種簡單演算法程式碼實現五一期間無聊時想起去年考研複試有一道上機題目當時沒作出來，於是一時興起想重新拾起看看是當時太緊張，還是自己能力不足。然後發現這道題目還真稍微有些難度，相當於一道數獨問題(sudoku)的簡化版。自己想來想去也只能想到兩種演算法，一種是拿剩餘元素做全排列測試，一種是回溯法測試。最後只實現了一個全排 ID3的REP（Reduced Error Pruning）剪枝程式碼詳細解釋+周志華《機器學習》決策樹圖4.5、圖4.6、圖4.7繪製處理資料物件:離散型資料資訊計算方式：熵資料集：西瓜資料集2.0共17條資料訓練集（用來建立決策樹）：西瓜資料集2.0中的第1,2,3,6,7,10,14,15,16,17,4 請注意，書上說是10條，其實是上面列出的11條。驗證集（用來對決策樹剪枝）：西瓜資料集2.0中的5,8 梯度下降演算法過程詳細解讀　　看了很多博文，一談到梯度下降，大多都在畫圖，類比“下山”。對於一開始想要了解“梯度下降”是個什麼玩意兒時，這種類比法是非常有助於理解的。但是，當我大概知道了梯度下降是什麼東西之後，我就好奇了，梯度下降究竟是怎樣尋找到模型的最優引數的？不能一想到梯度下降，腦海中就只有“下山”的畫面，“下山”不是目的，目的在 4.支援向量機（SVM）演算法(下） 1.SVM演算法的特點 1.1 訓練好的模型的演算法複雜度是由支援向量的個數決定的，而不是由資料的維度決定的。所有SVM不太容易產生overfitting 1.2 SVM訓練出來的模型完全依賴於支援向量（Support Vectors），即使訓練集裡面所有非支援向量的點都 3.支援向量機（SVM）演算法(上） SVM 1.基本概念支援向量機（Support Vector Machine, SVM）的基本模型是在特徵空間上找到最佳的分離超平面使得訓練集上正負樣本間隔最大。SVM是用來解決二分類問題的有監督學習演算法，在引入了核方法之後SVM也可以用來解決非線性問題。一般SVM有下面三搜尋基礎教學 Mysql入門 Sql入門 Android入門 Docker入門 Go語言入門 Ruby程式入門 Python入門 Python進階 Django入門 Python爬蟲入門最近訪問首頁前端設計程式設計免費資源實用技巧資料庫資訊字典 Copyright © 2002-2020 程式人生 796T.COM All rights reserved.

SVM SMO演算法程式碼詳細剖析

演算法實現

一：本文要結合SVM理論部分來看即筆者另一篇https://blog.csdn.net/weixin_42001089/article/details/83276714

二：有了理論部分下面就是直接程式碼啦，本文用四部分進行介紹：最簡版的SMO，改進版platt SMO，核函式，sklearn庫的SVM，四部分以%%%%%%%分開，採取的順序是先給程式碼及結果，然後分析

三：這裡程式碼大部分來自於Peter Harrington編寫的Machine Learning in Action

其網路資源https://www.manning.com/books/machine-learning-in-action

四：程式碼中需要注意的一點就是採用啟發式來尋找需要優化的

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

首先看一下最簡版的smo優化演算法：

這裡有兩個py檔案，一個是用來構造SVM的，一個是用來測試的：

MySVM:

接著是測試函式（MyTest）：

執行結果：

接下來一步步分析MySVM中的程式碼

首次看兩個簡單的輔助函式，第一個函式的作用就是用來選擇對的（即尋找i，j這一對）

第二個函式就是為了將規劃到[0,C]範圍內，對應到理論推導部分的：

接下來就是smo演算法的最簡版本：

接下來的calcWs函式作用是:根據訓練出來的生成w：

接下來視覺化看一下結果showClassifer：

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Platt SMO：

其是SMO演算法的一個改進版，速度更快。

下面來看一下具體程式碼：

smoP：

接著還是測試函式（MyTest）：

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

核函式

核函式的作用細節請看推導部分，核函式種類很多，這裡看一下最常用的徑向基高斯（RBF）核函式

最後寫一個簡單的呼叫sklearn庫的SVM程式：

結尾給一下我們用的資料集，方便大家實驗：

Train_data:

相關推薦

四：程式碼中需要注意的一點就是採用啟發式來尋找需要優化的 $\alpha$

首次看兩個簡單的輔助函式，第一個函式的作用就是用來選擇 $\alpha$ 對的（即尋找i，j這一對）

第二個函式就是為了將 $\alpha$ 規劃到[0,C]範圍內，對應到理論推導部分的：

接下來的calcWs函式作用是:根據訓練出來的 $\alpha$ 生成w：