《演算法導論》之動態規劃重構解
阿新 • • 發佈:2018-12-11
動態規劃(dynamic programming)就是把問題分解成一個個的子問題,然後對子問題進行求解。下面用通俗易懂的語言來解釋下動態規劃中關於重構解的理解。既儲存最優切割收益也儲存切割方案!
重構解
1、儲存最優切割收益也儲存切割方案的演算法
用 s[ j ] = i 來表示,長度為 j 的鋼條(當然在構建模型的時候也可以是其他含義)所得的最優解為 i 。
上述思想寫成BOTTOM-UP-CUT-ROD擴充套件版本如下:

- 第3句:求每種長度的情況的鋼條第一段切割的最優解。
- 第4句:初始化最優解值為負無窮。
- 第5句:從長度為 1 開始遍歷,一直到整根鋼條長度。計算出第一段長度該切割成多長才能獲得最優解,儲存在
s [ j ]=i中。 - 第6句:
q代表最優解收益,p[ i ] + r[ j - i ]表示切割下的第一段長度為i,剩下鋼條長度j - i的最大收益為r[ j - i ],因此總收益即為p[ i ] + r[ j - i ]。因此,當q<p[ i ] + r[ j - i ]的時候,更新最優情況,s[ j ] = i即切割第一段長度為i時獲益最大。 - 當遍歷完所有的情況,即可知道當前長度為
j的鋼條第一段切割多長可獲得最優收益。 因此,在本演算法中,不僅儲存了最優收益值p,還儲存了第一段切割長度(遞迴操作後,即可知道總的切割方案了),也即第10 句返回的r(最大收益)和s(切割方案)。
上述方案和BOTTOM-UP-CUT-ROD很相似,差別只是在第一行建立了陣列s(第一句),並將求解規模為 j 的子問題時,將第一段鋼條的最優切割長度 i 儲存在s[ j ]中了(第8句)。
2、呼叫上述函式並輸出鋼條切割方案 s 、最大收益 r

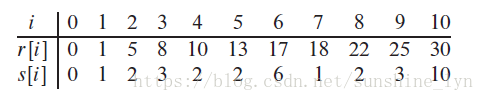
參考資料: [1].《演算法導論》第三版
