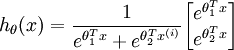Softmax演算法:邏輯迴歸的擴充套件
簡介
在本節中,我們介紹Softmax迴歸模型,該模型是logistic迴歸模型在多分類問題上的推廣,在多分類問題中,類標籤 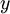 可以取兩個以上的值。
Softmax迴歸模型對於諸如MNIST手寫數字分類等問題是很有用的,該問題的目的是辨識10個不同的單個數字。Softmax迴歸是有監督的,不過後面也會介紹它與深度學習/無監督學習方法的結合。(譯者注: MNIST 是一個手寫數字識別庫,由NYU 的Yann LeCun 等人維護。http://yann.lecun.com/exdb/mnist/ )
可以取兩個以上的值。
Softmax迴歸模型對於諸如MNIST手寫數字分類等問題是很有用的,該問題的目的是辨識10個不同的單個數字。Softmax迴歸是有監督的,不過後面也會介紹它與深度學習/無監督學習方法的結合。(譯者注: MNIST 是一個手寫數字識別庫,由NYU 的Yann LeCun 等人維護。http://yann.lecun.com/exdb/mnist/ )
回想一下在 logistic 迴歸中,我們的訓練集由 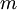 個已標記的樣本構成:
個已標記的樣本構成: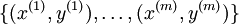 ,其中輸入特徵
,其中輸入特徵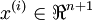 。(我們對符號的約定如下:特徵向量
。(我們對符號的約定如下:特徵向量 
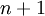 ,其中
,其中 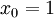 對應截距項
。) 由於 logistic 迴歸是針對二分類問題的,因此類標記
對應截距項
。) 由於 logistic 迴歸是針對二分類問題的,因此類標記 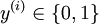 。假設函式(hypothesis
function) 如下:
。假設函式(hypothesis
function) 如下:
我們將訓練模型引數  ,使其能夠最小化代價函式 :
,使其能夠最小化代價函式 :
在 softmax迴歸中,我們解決的是多分類問題(相對於 logistic 迴歸解決的二分類問題),類標 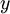 可以取
可以取  個不同的值(而不是
2 個)。因此,對於訓練集
個不同的值(而不是
2 個)。因此,對於訓練集 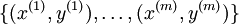 ,我們有
,我們有 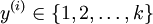 。(注意此處的類別下標從
1 開始,而不是 0)。例如,在 MNIST 數字識別任務中,我們有
。(注意此處的類別下標從
1 開始,而不是 0)。例如,在 MNIST 數字識別任務中,我們有 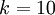 個不同的類別。
個不同的類別。
對於給定的測試輸入  ,我們想用假設函式針對每一個類別j估算出概率值
,我們想用假設函式針對每一個類別j估算出概率值 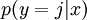
 的每一種分類結果出現的概率。因此,我們的假設函式將要輸出一個
的每一種分類結果出現的概率。因此,我們的假設函式將要輸出一個  維的向量(向量元素的和為1)來表示這
維的向量(向量元素的和為1)來表示這  個估計的概率值。
具體地說,我們的假設函式
個估計的概率值。
具體地說,我們的假設函式 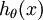 形式如下:
形式如下:
其中 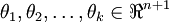 是模型的引數。請注意
是模型的引數。請注意 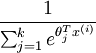 這一項對概率分佈進行歸一化,使得所有概率之和為
1 。
這一項對概率分佈進行歸一化,使得所有概率之和為
1 。
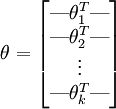
為了方便起見,我們同樣使用符號  來表示全部的模型引數。在實現Softmax迴歸時,將
來表示全部的模型引數。在實現Softmax迴歸時,將  用一個
用一個 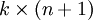 的矩陣來表示會很方便,該矩陣是將
的矩陣來表示會很方便,該矩陣是將 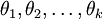 按行羅列起來得到的,如下所示:
按行羅列起來得到的,如下所示:
代價函式
現在我們來介紹 softmax 迴歸演算法的代價函式。在下面的公式中,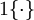 是示性函式,其取值規則為:
是示性函式,其取值規則為:
值為真的表示式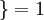
, 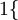 值為假的表示式
值為假的表示式 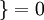 。舉例來說,表示式
。舉例來說,表示式 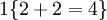 的值為1
,
的值為1
,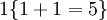 的值為 0。我們的代價函式為:
的值為 0。我們的代價函式為:
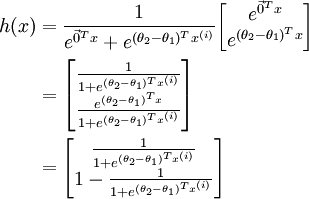
值得注意的是,上述公式是logistic迴歸代價函式的推廣。logistic迴歸代價函式可以改為:
可以看到,Softmax代價函式與logistic 代價函式在形式上非常類似,只是在Softmax損失函式中對類標記的  個可能值進行了累加。注意在Softmax迴歸中將
個可能值進行了累加。注意在Softmax迴歸中將  分類為類別
分類為類別  的概率為:
的概率為:
-
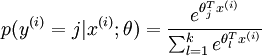 .
.
對於  的最小化問題,目前還沒有閉式解法。因此,我們使用迭代的優化演算法(例如梯度下降法,或
L-BFGS)。經過求導,我們得到梯度公式如下:
的最小化問題,目前還沒有閉式解法。因此,我們使用迭代的優化演算法(例如梯度下降法,或
L-BFGS)。經過求導,我們得到梯度公式如下:
讓我們來回顧一下符號 "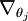 " 的含義。
" 的含義。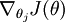 本身是一個向量,它的第
本身是一個向量,它的第  個元素
個元素 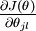 是
是  對
對 的第
的第  個分量的偏導數。
個分量的偏導數。
有了上面的偏導數公式以後,我們就可以將它代入到梯度下降法等演算法中,來最小化  。 例如,在梯度下降法的標準實現中,每一次迭代需要進行如下更新:
。 例如,在梯度下降法的標準實現中,每一次迭代需要進行如下更新: 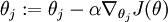 (
(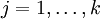 )。
)。
當實現 softmax 迴歸演算法時, 我們通常會使用上述代價函式的一個改進版本。具體來說,就是和權重衰減(weight decay)一起使用。我們接下來介紹使用它的動機和細節。
Softmax迴歸模型引數化的特點
Softmax 迴歸有一個不尋常的特點:它有一個“冗餘”的引數集。為了便於闡述這一特點,假設我們從引數向量  中減去了向量
中減去了向量 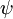 ,這時,每一個
,這時,每一個  都變成了
都變成了 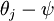 (
(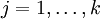 )。此時假設函式變成了以下的式子:
)。此時假設函式變成了以下的式子:
換句話說,從  中減去
中減去 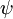 完全不影響假設函式的預測結果!這表明前面的
softmax 迴歸模型中存在冗餘的引數。更正式一點來說, Softmax 模型被過度引數化了。對於任意一個用於擬合數據的假設函式,可以求出多組引數值,這些引數得到的是完全相同的假設函式
完全不影響假設函式的預測結果!這表明前面的
softmax 迴歸模型中存在冗餘的引數。更正式一點來說, Softmax 模型被過度引數化了。對於任意一個用於擬合數據的假設函式,可以求出多組引數值,這些引數得到的是完全相同的假設函式 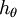 。
。
進一步而言,如果引數 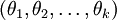 是代價函式
是代價函式  的極小值點,那麼
的極小值點,那麼 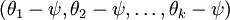 同樣也是它的極小值點,其中
同樣也是它的極小值點,其中 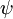 可以為任意向量。因此使
可以為任意向量。因此使  最小化的解不是唯一的。(有趣的是,由於
最小化的解不是唯一的。(有趣的是,由於  仍然是一個凸函式,因此梯度下降時不會遇到區域性最優解的問題。但是
Hessian 矩陣是奇異的/不可逆的,這會直接導致採用牛頓法優化就遇到數值計算的問題)
仍然是一個凸函式,因此梯度下降時不會遇到區域性最優解的問題。但是
Hessian 矩陣是奇異的/不可逆的,這會直接導致採用牛頓法優化就遇到數值計算的問題)
注意,當 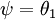 時,我們總是可以將
時,我們總是可以將 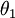 替換為
替換為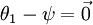 (即替換為全零向量),並且這種變換不會影響假設函式。因此我們可以去掉引數向量
(即替換為全零向量),並且這種變換不會影響假設函式。因此我們可以去掉引數向量 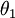 (或者其他
(或者其他  中的任意一個)而不影響假設函式的表達能力。實際上,與其優化全部的
中的任意一個)而不影響假設函式的表達能力。實際上,與其優化全部的 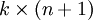 個引數
個引數 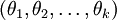 (其中
(其中 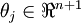 ),我們可以令
),我們可以令 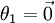 ,只優化剩餘的
,只優化剩餘的 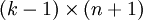 個引數,這樣演算法依然能夠正常工作。
個引數,這樣演算法依然能夠正常工作。
在實際應用中,為了使演算法實現更簡單清楚,往往保留所有引數  ,而不任意地將某一引數設定為
0。但此時我們需要對代價函式做一個改動:加入權重衰減。權重衰減可以解決 softmax 迴歸的引數冗餘所帶來的數值問題。
,而不任意地將某一引數設定為
0。但此時我們需要對代價函式做一個改動:加入權重衰減。權重衰減可以解決 softmax 迴歸的引數冗餘所帶來的數值問題。
權重衰減
我們通過新增一個權重衰減項 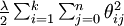 來修改代價函式,這個衰減項會懲罰過大的引數值,現在我們的代價函式變為:
來修改代價函式,這個衰減項會懲罰過大的引數值,現在我們的代價函式變為:
有了這個權重衰減項以後 (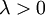 ),代價函式就變成了嚴格的凸函式,這樣就可以保證得到唯一的解了。
此時的 Hessian矩陣變為可逆矩陣,並且因為
),代價函式就變成了嚴格的凸函式,這樣就可以保證得到唯一的解了。
此時的 Hessian矩陣變為可逆矩陣,並且因為 是凸函式,梯度下降法和 L-BFGS
等演算法可以保證收斂到全域性最優解。
是凸函式,梯度下降法和 L-BFGS
等演算法可以保證收斂到全域性最優解。
為了使用優化演算法,我們需要求得這個新函式  的導數,如下:
的導數,如下:
通過最小化  ,我們就能實現一個可用的 softmax 迴歸模型。
,我們就能實現一個可用的 softmax 迴歸模型。
Softmax迴歸與Logistic 迴歸的關係
當類別數 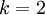 時,softmax
迴歸退化為 logistic 迴歸。這表明 softmax 迴歸是 logistic 迴歸的一般形式。具體地說,當
時,softmax
迴歸退化為 logistic 迴歸。這表明 softmax 迴歸是 logistic 迴歸的一般形式。具體地說,當 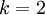 時,softmax
迴歸的假設函式為:
時,softmax
迴歸的假設函式為:
利用softmax迴歸引數冗餘的特點,我們令 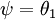 ,並且從兩個引數向量中都減去向量
,並且從兩個引數向量中都減去向量 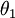 ,得到:
,得到:
因此,用 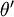 來表示
來表示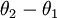 ,我們就會發現
softmax 迴歸器預測其中一個類別的概率為
,我們就會發現
softmax 迴歸器預測其中一個類別的概率為 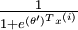 ,另一個類別概率的為
,另一個類別概率的為 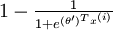 ,這與
logistic迴歸是一致的。
,這與
logistic迴歸是一致的。
Softmax 迴歸 vs. k 個二元分類器
如果你在開發一個音樂分類的應用,需要對k種類型的音樂進行識別,那麼是選擇使用 softmax 分類器呢,還是使用 logistic 迴歸演算法建立 k 個獨立的二元分類器呢?
這一選擇取決於你的類別之間是否互斥,例如,如果你有四個類別的音樂,分別為:古典音樂、鄉村音樂、搖滾樂和爵士樂,那麼你可以假設每個訓練樣本只會被打上一個標籤(即:一首歌只能屬於這四種音樂型別的其中一種),此時你應該使用類別數 k = 4 的softmax迴歸。(如果在你的資料集中,有的歌曲不屬於以上四類的其中任何一類,那麼你可以新增一個“其他類”,並將類別數 k 設為5。)
如果你的四個類別如下:人聲音樂、舞曲、影視原聲、流行歌曲,那麼這些類別之間並不是互斥的。例如:一首歌曲可以來源於影視原聲,同時也包含人聲 。這種情況下,使用4個二分類的 logistic 迴歸分類器更為合適。這樣,對於每個新的音樂作品 ,我們的演算法可以分別判斷它是否屬於各個類別。
現在我們來看一個計算視覺領域的例子,你的任務是將影象分到三個不同類別中。(i) 假設這三個類別分別是:室內場景、戶外城區場景、戶外荒野場景。你會使用sofmax迴歸還是 3個logistic 迴歸分類器呢? (ii) 現在假設這三個類別分別是室內場景、黑白圖片、包含人物的圖片,你又會選擇 softmax 迴歸還是多個 logistic 迴歸分類器呢?
在第一個例子中,三個類別是互斥的,因此更適於選擇softmax迴歸分類器 。而在第二個例子中,建立三個獨立的 logistic迴歸分類器更加合適。
中英文對照
- Softmax迴歸 Softmax Regression
- 有監督學習 supervised learning
- 無監督學習 unsupervised learning
- 深度學習 deep learning
- logistic迴歸 logistic regression
- 截距項 intercept term
- 二元分類 binary classification
- 型別標記 class labels
- 估值函式/估計值 hypothesis
- 代價函式 cost function
- 多元分類 multi-class classification
- 權重衰減 weight decay
中文譯者
曾俊瑀([email protected]), 王方([email protected]),王文中([email protected])
相關推薦
Softmax演算法:邏輯迴歸的擴充套件
簡介 在本節中,我們介紹Softmax迴歸模型,該模型是logistic迴歸模型在多分類問題上的推廣,在多分類問題中,類標籤 可以取兩個以上的值。 Softmax迴歸模型對於諸如MNIST手寫數字分類等問題是很有用的,該問題的目的是辨識10個不同的單個數字。Softmax迴歸是有監督的
數學推導+純Python實現機器學習演算法:邏輯迴歸
自本系列第一講推出以來,得到了不少同學的反響和贊成,也有同學留言說最好能把數學推導部分寫的詳細點,筆者只能說盡力,因為打公式實在是太浪費時間了。。本節要和大家一起學習的是邏輯(logistic)迴歸模型,繼續按照手推公式+純 Python 的寫作套路。 邏輯迴歸本質上跟邏輯這個詞不是很搭邊,叫這個名字完
sklearn分類器演算法:邏輯迴歸及案例分析
分類演算法之邏輯迴歸邏輯迴歸(Logistic Regression),簡稱LR。它的特點是能夠是我們的特徵輸入集合轉化為0和1這兩類的概率。一般來說,迴歸不用在分類問題上,因為迴歸是連續型模型,而且受噪聲
機器學習演算法之: 邏輯迴歸 logistic regression (LR)
by joey周琦 LR介紹 邏輯迴歸屬於probabilistic discriminative model這一類的分類演算法 probabilistic discriminative mode這類演算法的思路如下: - 直接建模 P(Ck|x)
機器學習筆記 第6課:邏輯迴歸演算法
邏輯迴歸是機器學習從統計領域借用的又一項技術。它是二元分類問題(即只有兩種型別的分類問題)的首選方法。 邏輯迴歸和線性迴歸的類似之處在於,其目標是找到每個輸入變數的權重係數。 與線性迴歸的不同點是,邏輯函式是非線性函式,邏輯迴歸使用非線性的邏輯函式對輸出結果進行轉換。
機器學習方法(五):邏輯迴歸Logistic Regression,Softmax Regression
歡迎轉載,轉載請註明:本文出自Bin的專欄blog.csdn.net/xbinworld。 技術交流QQ群:433250724,歡迎對演算法、技術、應用感興趣的同學加入。 前面介紹過線性迴歸的基本知識,線性迴歸因為它的簡單,易用,且可以求出閉合解,被廣泛地
機器學習演算法(一):邏輯迴歸模型(Logistic Regression, LR)
轉自:https://blog.csdn.net/weixin_39910711/article/details/81607386 線性分類器:模型是引數的線性函式,分類平面是(超)平面;非線性分類器:模型分介面可以是曲面或者超平面的組合。 典型的線性分類器有感知機,LDA,邏輯斯特迴歸,SVM
入門機器學習演算法交易:邏輯迴歸的理論和交易
目前股市的量化交易已經成為了人工智慧研究的一個熱門領域,很多計算機人員都想利用自己的程式設計技術去量化交易,也有很多的金融人員想要學習程式設計技術。如果你想知道一些方法論上面的知識,可以檢視我上一個文章。本次 Chat,文章會一步一步向你介如何用最簡單的邏輯迴歸在股票資料上面
演算法學習——邏輯迴歸(Logistic Regression)
1.Logistic Regression 1.1什麼是迴歸? 英文單詞Regression翻譯成中文“迴歸”,那什麼是迴歸呢?事實上,在Logistic迴歸出現以前,人們最先引入的是線性迴歸。瞭解二者之間的來龍去脈將幫助你更深刻地認識Logistic迴歸。 迴歸一詞最早由英國科學家
機器學習演算法2_邏輯迴歸
文章目錄 1 邏輯迴歸 1.1 概念 1.2 推導方法 1.2.1 模型 - Sigmoid 分佈函式 1.2.2 目標函式 - 對數損失函式 1.2.3 求解方法 1.2.3.1
機器學習6:邏輯迴歸到深度學習的思考
如下圖,出現了不可分的情形: , 表明x1與x2並不是兩個很好的特徵,可以從如下方面進行思考: 1、通過特徵變換(將x1與x2通過各種運算組合得到新的可分特徵x3與x4),將模型變成線性可分的模型。比如將上述點轉換成每個點到一個固定座標的距離,得到如下情形: ,變成線性可分。 2
機器學習5:邏輯迴歸之多分類Multi-class classification
上一節講解了邏輯迴歸中的二分類問題的原理與步驟,本節講解多分類問題。 以三個class分類為例,過程如圖所示: 原理性推導省略。 1、如圖1所示,對於每個類別,各分配一個線性模型,通過softmax處理得到每個類別的輸出概率y,且所有y的和等於1; 2、如圖2所示,輸出的
機器學習4:邏輯迴歸與線性迴歸
邏輯迴歸與線性迴歸求解過程: 總體來說,迴歸過程都分三步: 1、Model 2、Loss Fuction 3、Gradient Decent 分析: 1、Model:線性迴歸中,模型為線性方程,取值範圍無窮大;邏輯迴歸中,通過sigmod函式函式將線性方程z轉化成概率(
演算法模型---邏輯迴歸學習
邏輯迴歸的特點 邏輯迴歸的用途 第一用來預測,第二尋找因變數的影響因素。 邏輯迴歸的適用範圍 資料型別 邏輯迴歸的優點 原理的相對簡單,可解釋性強等優點,它還可以作為眾多整合演算法以及深度學習的基本組成單位 Logistic迴歸分析報告結果解讀分析 邏輯迴歸的
機器學習基本知識(二):邏輯迴歸
一、分類和迴歸 迴歸(Regression)和分類(Classification)是機器學習中的兩大類問題,迴歸問題的輸出是連續的,而分類的輸出則是代表不同類別的有限個離散數值。
ML模型2:邏輯迴歸
一些迴歸演算法可以用來處理分類問題,以及一些分類演算法可以進行迴歸預測,邏輯迴歸就屬於前者。邏輯迴歸一般通過估計一個概率值,來表示一個樣本屬於某一類的概率。假如一個樣本屬於某一類的概率大於50%,那麼就判該樣本屬於這一類。 優點:計算代價不高,易於理解和實現。
機器學習:邏輯迴歸詳細推導
如今機器學習、深度學習可謂炙手可熱,人工智慧也確實開始影響、改變著我們的生活。正因如此,很多同學開始接觸或者學習這方面的知識。機器學習的入門是有難度的,因為它不僅要求你會編碼,還要你熟悉高等數學,比如線性代數,微積分等,除此之外,還要懂統計學。如果你想入門機器學習,那麼一定要好好學習邏輯迴歸。原因如
機器學習筆記3:邏輯迴歸
機器學習筆記3:邏輯迴歸 Andrew Ng機器學習課程學習筆記3 邏輯迴歸就是分類問題,比如把郵件標示為垃圾郵件和正常郵件,判斷腫瘤是良性的還是惡性的. Sigmoid function 線性迴歸方程中,hθ(x) 的取值y是連續的,而邏輯迴歸中輸出則是離散的。以兩個類別
tensorflow100天-第4天:邏輯迴歸
程式碼 # coding:utf-8 # zhong import tensorflow as tf # Import MINST data from tensorflow.examples.tutorials.mnist import input_data mnist = inpu
大叔學ML第五:邏輯迴歸
目錄 基本形式 代價函式 用梯度下降法求\(\vec\theta\) 擴充套件 基本形式 邏輯迴歸是最常用的分類模型,線上性迴歸基礎之上擴充套件而來,是一種廣義線性迴歸。下面舉例說明什麼是邏輯迴歸:假設我們有樣本如下(是我程式設計生成的資料): 我們要做的是找到一個決策邊

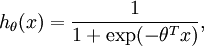
![\begin{align}J(\theta) = -\frac{1}{m} \left[ \sum_{i=1}^m y^{(i)} \log h_\theta(x^{(i)}) + (1-y^{(i)}) \log (1-h_\theta(x^{(i)})) \right]\end{align}](http://deeplearning.stanford.edu/wiki/images/math/f/a/6/fa6565f1e7b91831e306ec404ccc1156.png)
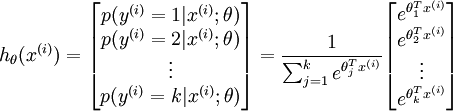
![\begin{align}J(\theta) = - \frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{j=1}^{k} 1\left\{y^{(i)} = j\right\} \log \frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{ \theta_l^T x^{(i)} }}\right]\end{align}](http://deeplearning.stanford.edu/wiki/images/math/7/6/3/7634eb3b08dc003aa4591a95824d4fbd.png)
![\begin{align}J(\theta) &= -\frac{1}{m} \left[ \sum_{i=1}^m (1-y^{(i)}) \log (1-h_\theta(x^{(i)})) + y^{(i)} \log h_\theta(x^{(i)}) \right] \\&= - \frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{j=0}^{1} 1\left\{y^{(i)} = j\right\} \log p(y^{(i)} = j | x^{(i)} ; \theta) \right]\end{align}](http://deeplearning.stanford.edu/wiki/images/math/5/4/9/5491271f19161f8ea6a6b2a82c83fc3a.png)
![\begin{align}\nabla_{\theta_j} J(\theta) = - \frac{1}{m} \sum_{i=1}^{m}{ \left[ x^{(i)} \left( 1\{ y^{(i)} = j\} - p(y^{(i)} = j | x^{(i)}; \theta) \right) \right] }\end{align}](http://deeplearning.stanford.edu/wiki/images/math/5/9/e/59ef406cef112eb75e54808b560587c9.png)
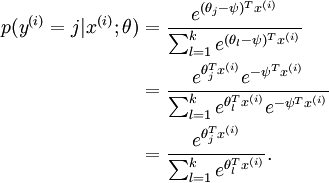
![\begin{align}J(\theta) = - \frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{j=1}^{k} 1\left\{y^{(i)} = j\right\} \log \frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{ \theta_l^T x^{(i)} }} \right] + \frac{\lambda}{2} \sum_{i=1}^k \sum_{j=0}^n \theta_{ij}^2\end{align}](http://deeplearning.stanford.edu/wiki/images/math/4/7/1/471592d82c7f51526bb3876c6b0f868d.png)
![\begin{align}\nabla_{\theta_j} J(\theta) = - \frac{1}{m} \sum_{i=1}^{m}{ \left[ x^{(i)} ( 1\{ y^{(i)} = j\} - p(y^{(i)} = j | x^{(i)}; \theta) ) \right] } + \lambda \theta_j\end{align}](http://deeplearning.stanford.edu/wiki/images/math/3/a/f/3afb4b9181a3063ddc639099bc919197.png)