【小白學遊戲常用演算法】二、A*啟發式搜尋演算法
在上一篇部落格中,我們一起學習了隨機迷宮演算法,在本篇部落格中,我們將一起了解一下尋路演算法中常用的A*演算法。
通常情況下,迷宮尋路演算法可以使用深度優先或者廣度優先演算法,但是由於效率的原因,不會直接使用這些演算法,在路徑搜尋演算法中最常見的就是A*尋路演算法。使用A*演算法的魅力之處在於它不僅能找到地圖中從A到B的一條路徑,還能保證找到的是一條最短路徑,它是一種常見的啟發式搜尋演算法,類似於Dijkstra演算法一樣的最短路徑查詢演算法,很多遊戲應用中的路徑搜尋基本都是採用這種演算法或者是A*演算法的變種。
下面我們來了解一下A*演算法相關的理論知識:

如圖,我們需要在迷宮中找到A點到B點的一條最短的可以通過的路徑,A和B直接被一面牆堵住了。在上一篇部落格中我們說到了,地圖是有二維陣列組成的,牆表示不能通過的地方,用1表示,A*演算法所要做的就是從A找到一條最短的通向B的路徑。當然,不能從牆上飛過去,也不能瞬移到B。只能每次移動一個格子,一步一步地移動到B目標位置。問題在於,每次移動一格的時候,有上下左右四個方向,這裡我們限制物體斜向移動,如何選擇下一個移動方向呢?按照我們的想法,不就是找一條離目標最近的路嗎?那我們可以在這四個方向中,找一個最接近目標點的位置,當然,還要考慮障礙因素,基於這個思想,A*演算法採用了以下的搜尋步驟來實現:
1.首先把起始位置點加入到一個稱為“open List”的列表,在尋路的過程中,目前,我們可以認為open List這個列表會存放許多待測試的點,這些點是通往目標點的關鍵,以後會逐漸往裡面新增更多的測試點,同時,為了效率考慮,通常這個列表是個已經排序的列表。
2.如果open List列表不為空,則重複以下工作:
(1)找出open List中通往目標點代價最小的點作為當前點;
(2)把當前點放入一個稱為close List的列表;
(3)對當前點周圍的4個點每個進行處理(這裡是限制了斜向的移動),如果該點是可以通過並且該點不在close List列表中,則處理如下;
(4)如果該點正好是目標點,則把當前點作為該點的父節點,並退出迴圈,設定已經找到路徑標記;
(5)如果該點也不在open List中,則計算該節點到目標節點的代價,把當前點作為該點的父節點,並把該節點新增到open List中;
(6)如果該點已經在open List中了,則比較該點和當前點通往目標點的代價,如果當前點的代價更小,則把當前點作為該點的父節點,同時,重新計算該點通往目標點的代價,並把open List重新排序;
3.完成以上迴圈後,如果已經找到路徑,則從目標點開始,依次查詢每個節點的父節點,直到找到開始點,這樣就形成了一條路徑。
以上,就是A*演算法的全部步驟,按照這個步驟,就可以得到一條正確的路徑。這裡有一個關鍵的地方,就是如何計算每個點通往目標點的代價,之所以稱為A*演算法為啟發式搜尋,就是因為通過評估這個代價值來搜尋最近的路徑,對於任意一個點的代價值,在A*演算法中通常使用下列的公式計算:
代價F=G+H
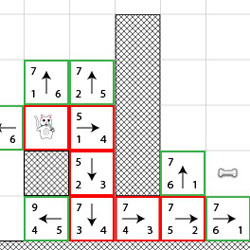
在這裡,F表示通往目標點的代價,G表示從起始點移動到該點的距離,H則表示從該點到目標點的距離,比如圖中,可以看到小狗的附近格子的代價值,其中左上角的數字代表F值,左下角的數字代表G值,右下角的數字代表H值。拿小狗上方的格子來舉例,G=1,表示從小狗的位置到該點的距離為1個格子,H=6,表示從小狗到骨頭的距離是6個格子,則F=G+H=7。在此處,距離的演算法是採用曼哈頓距離,它計算從當前格子到目的格子之間水平和垂直的方格的數量總和,例如在平面上,座標(x1,y1)的點和座標(x2,y2)的點的曼哈頓距離為:
|x1-x2|+|y1-y2|
當然,距離的演算法也可以採用其他的方法,實際在遊戲中,這個移動的代價除了要考慮距離因素外,還要考慮當前格子的遊戲屬性。比如有的格子表示水路、草地、陸地,這些有可能影響人物移動的速度,實際計算的時候還要把這些考慮在內。
另一個需要注意的就是,在計算這個距離的時候是毋須考慮障礙因素的,因為在以上A*演算法步驟中會剔除掉障礙。
這樣,按照前面所說的A*演算法的步驟,第一次迴圈open List的時候,把A點作為當前點,同時把A周圍的四個點放入到open List中。第二次迴圈的時候把A右邊的點作為當前點,該點的父節點就是A,這是處理當前點的時候,只需要把當前點的上下兩個點放入open List中,因為左邊的A已經在close List中,而右邊的是牆,所以直接被忽略。
A*的演算法具體程式碼如下:
1 //地圖工具
2 var _MapUtil = win.MapUtil =
3 {
4 //定義點物件
5 Point:function(x,y)
6 {
7 this.x = x;
8 this.y = y;
9 this.parent = null;
10 this.f = 0;
11 this.g = 0;
12 this.h=0;
13 //當前點狀態,0:表示在openlist 1:表示closelist,-1表示還沒處理
14 this.state=-1;
15 //flag表明該點是否可通過
16 this.flag = 0;
17 },
18 //產生隨機迷宮
19 primMaze:function(r,c)
20 {
21 //初始化陣列
22 function init(r,c)
23 {
24 var a = new Array(2*r+1);
25 //全部置1
26 for(var i=0,len=a.length;i<len;i++)
27 {
28 var cols = 2*c+1;
29 a[i]= new Array(cols);
30 ArrayUtil.fillWith(a[i],1);
31 }
32 //中間格子為0
33 for(var i=0;i<r;i++)
34 for(var j=0;j<c;j++)
35 {
36 a[2*i+1][2*j+1] = 0;
37 }
38 return a;
39 }
40 //處理陣列,產生最終的陣列
41 function process(arr)
42 {
43 //acc存放已訪問佇列,noacc存放沒有訪問佇列
44 var acc = [],noacc = [];
45 var r = arr.length>>1,c=arr[0].length>>1;
46 var count = r*c;
47 for(var i=0;i<count;i++){noacc[i]=0;}
48 //定義空單元上下左右偏移
49 var offs=[-c,c,-1,1],offR=[-1,1,0,0],offC=[0,0,-1,1];
50 //隨機從noacc取出一個位置
51 var pos = MathUtil.randInt(count);
52 noacc[pos]=1;
53 acc.push(pos);
54 while(acc.length<count)
55 {
56 var ls = -1,offPos = -1;
57 offPos = -1;
58 //找出pos位置在二維陣列中的座標
59 var pr = pos/c|0,pc=pos%c,co=0,o=0;
60 //隨機取上下左右四個單元
61 while(++co<5)
62 {
63 o = MathUtil.randInt(0,5);
64 ls =offs[o]+pos;
65 var tpr = pr+offR[o];
66 var tpc = pc+offC[o];
67 if(tpr>=0&&tpc>=0&&tpr<=r-1&&tpc<=c-1&&noacc[ls]==0){ offPos = o;break;}
68 }
69 if(offPos<0)
70 {
71
72 pos = acc[MathUtil.randInt(acc.length)];
73 }
74 else
75 {
76 pr = 2*pr+1;
77 pc = 2*pc+1;
78 //相鄰空單元中間的位置置0
79 arr[pr+offR[offPos]][pc+offC[offPos]]=0;
80 pos = ls;
81 noacc[pos] = 1;
82 acc.push(pos);
83 }
84 }
85 }
86 var a = init(r,c);
87 process(a);
88 return a;
89 },
90 //把普通二維陣列(全部由1,0表示)的轉換成a*所需要的點陣列
91 convertArrToAS:function(arr)
92 {
93 var r = arr.length,c=arr[0].length;
94 var a = new Array(r);
95 for(var i=0;i<r;i++)
96 {
97 a[i] = new Array(c);
98 for(var j=0;j<c;j++)
99 {
100 var pos = new MapUtil.Point(i,j);
101 pos.flag = arr[i][j];
102 a[i][j]=pos;
103 }
104 }
105 return a;
106 },
107 //A*演算法,pathArr表示最後返回的路徑
108 findPathA:function(pathArr,start,end,row,col)
109 {
110 //新增資料到排序陣列中
111 function addArrSort(descSortedArr,element,compare)
112 {
113 var left = 0;
114 var right = descSortedArr.length-1;
115 var idx = -1;
116 var mid = (left+right)>>1;
117 while(left<=right)
118 {
119 var mid = (left+right)>>1;
120 if(compare(descSortedArr[mid],element)==1)
121 {
122 left = mid+1;
123 }
124 else if(compare(descSortedArr[mid],element)==-1)
125 {
126 right = mid-1;
127 }
128 else
129 {
130 break;
131 }
132 }
133 for(var i = descSortedArr.length-1;i>=left;i--)
134 {
135 descSortedArr[i+1] = descSortedArr[i];
136 }
137 descSortedArr[left] = element;
138 return idx;
139 }
140 //判斷兩個點是否相同
141 function pEqual(p1,p2)
142 {
143 return p1.x==p2.x&&p1.y==p2.y;
144 }
145 //獲取兩個點距離,採用曼哈頓方法
146 function posDist(pos,pos1)
147 {
148 return (Math.abs(pos1.x-pos.x)+Math.abs(pos1.y-pos.y));
149 }
150 function between(val,min,max)
151 {
152 return (val>=min&&val<=max)
153 }
154 //比較兩個點f值大小
155 function compPointF(pt1,pt2)
156 {
157 return pt1.f-pt2.f;
158 }
159 //處理當前節點
160 function processCurrpoint(arr,openList,row,col,currPoint,destPoint)
161 {
162 //get up,down,left,right direct
163 var ltx = currPoint.x-1;
164 var lty = currPoint.y-1;
165 for(var i=0;i<3;i++)
166 for(var j=0;j<3;j++)
167 {
168 var cx = ltx+i;
169 var cy = lty+j;
170 if((cx==currPoint.x||cy==currPoint.y)&&between(ltx,0,row-1)&&between(lty,0,col-1))
171 {
172 var tp = arr[cx][cy];
173 if(tp.flag == 0 && tp.state!=1)
174 {
175 if(pEqual(tp,destPoint))
176 {
177 tp.parent = currPoint;
178 return true;
179 }
180 if(tp.state == -1)
181 {
182 tp.parent = currPoint;
183 tp.g= 1+currPoint.g;
184 tp.h= posDist(tp,destPoint);
185 tp.f = tp.h+tp.f;
186 tp.state = 0
187 addArrSort(openList,tp,compPointF);
188 }
189 else
190 {
191 var g = 1+currPoint.g
192 if(g<tp.g)
193 {
194 tp.parent = currPoint;
195 tp.g = g;
196 tp.f = tp.g+tp.h;
197 openList.quickSort(compPointF);
198 }
199 }
200 }
201 }
202 }
203 return false;
204 }
205 //定義openList
206 var openList = [];
207 //定義closeList
208 var closeList = [];
209 start = pathArr[start[0]][start[1]];
210 end = pathArr[end[0]][end[1]];
211 //新增開始節點到openList;
212 addArrSort(openList,start,compPointF);
213 var finded = false;
214 var tcount = 0;
215 while((openList.length>0))
216 {
217 var currPoint = openList.pop();
218 currPoint.state = 1;
219 closeList.push(currPoint);
220 finded = processCurrpoint(pathArr,openList,row,col,currPoint,end);
221 if(finded)
222 {
223 break;
224 }
225 }
226 if(finded)
227 {
228 var farr = [];
229 var tp = end.parent;
230 farr.push(end);
231 while(tp!=null)
232 {
233 farr.push(tp);
234 tp = tp.parent;
235 }
236 return farr;
237 }
238 else
239 {
240 return null;
241 }
242 }
243 }
運用上面的程式碼,我們可以實現一個簡單的迷宮尋路DEMO,使用者在迷宮中點選任意的地點,藍色的球體就會自動尋路移動到該點,如圖:


此DEMO的原始碼地址
A*演算法不僅可以應用在遊戲當中,同樣也可以應用到其他領域,比如車輛定位和行車自動導航,當然,這得需要另外的地理資訊資料支援。

