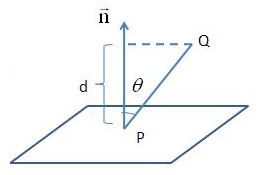
點到平面的距離公式推導
預備知識:
(1) 平面的一般表示式:
其中,n=(A,B,C)是平面的法向量,D決定了平面與原點之間的距離,當D=0時,平面經過原點。
(2) 向量的模(長度):
給定一個向量V=(x,y,z),則
(3) 向量的點積(內積):
給定兩個向量

點到直線的距離公式推導:
參考部落格:http://www.cnblogs.com/graphics/archive/2010/07/10/1774809.html
--------------------- 本文來自 懶懶的傑威 的CSDN 部落格 ,全文地址請點選:https://blog.csdn.net/u011483307/article/details/51034169?utm_source=copy
相關推薦
點到超平面距離公式 推導
idt ima .net || mage sub detail eight 技術 公式: d = |wx0 + b|/||w||2 推導: 參考文獻: https://blog.csdn.net/yutao03081/article/details/7
點到平面的距離公式推導
預備知識: (1) 平面的一般表示式: 其中,n=(A,B,C)是平面的法向量,D決定了平面與原點之間的距離,當D=0時,平面經過原點。 (2) 向量的模(長度): 給定一個向量V=(x,y,z),則 (3) 向量的點積(內積): 給定兩個向量和,
I型支援向量機SVM距離公式推導
關於支援向量機(SVM)I型中,對任意x0x_0x0來說,為何x0x_0x0到超平面ωTX+b=0\omega^TX+b=0ωTX+b=0的距離公式中,必滿足以下式子:∣ωTx0+b∣=1|\omega^Tx_0+b|=1∣ωTx0+b∣=1,??? 其實
二維空間點到直線垂足計算公式推導及Java實現——學習筆記
二維空間點到直線垂足計算公式推導及Java實現前言公式推導程式碼實現畫蛇添足 前言 簡單的公式推導,大概是高中程度的知識了。不管以前學的好不好,很久不用的東西,一上手還是有點懵的。推導一遍也是為了加深記憶。 公式推導 首先我們知道直線上兩點p1,p2: p1:(
分治法求解平面n點中距離最近的兩點
步驟4:將L-d~L+d內的點以y值排序,對於每一個點(x1,y1)找出y值在y1-d~y1+d內的所有點,計算距離為d'。 如果d'小於d,令d=d',最後的d值就是答案。 實驗1 遞迴與分治演算法 一,實驗目的和要求 (1)進一步掌握遞迴演算法的設計思想以及遞迴程式的除錯
根據經緯度計算兩點之間的距離的公式推導過程以及google.maps的測距函式
首先,你要想了解清楚經緯度的具體定義,看完後再往下看,便會一目瞭然。 將地球看成一個球體,A(WA,JA)、B(WB,JB)兩點分別為兩個點的位置,其中W為緯度,J為經度,O為球心,球半徑為R,過A點畫出A的緯度圈並與B所在的經度相交與點C,分別過B、C兩點做球心O所在直線
C++:點到線段的平面距離。點與點的平面距離。
LPoint是自己定義的點 //點(p0) 到線段(p1,p2)的距離 double GroundFilter::xj2DistancePointAndLine( LPoint p0, LPoint
POJ 2140 Herd Sums 公式推導
cpp true typedef 因數 固定 ostream highlight ring sum 題意:給出n<=1e7 求有多少個連續數之和等於k x+x+1+....x+k=n (k+1)k/2+(k+1)x=n (k+1)k+(k+1)2x=2*n (k
vijos - P1543極值問題(斐波那契數列 + 公式推導 + python)
找到 span add gin python3 abi pri n) fill P1543極值問題 Accepted 標簽:[顯示標簽] 背景 小銘的數學之旅2。 描寫敘述 已知m、n為整數,且滿足下列兩個條件: ①
vijos - P1302連續自然數和 (公式推導 + python)
.net ble tags ucid stat down bsp z-index fontsize P1302連續自然數和 Accepted 標簽:[顯示標簽] 描寫敘述 對一個給定的自然數M,求出所有的連續的自然數段(連續個數大於1)
解釋一下核主成分分析(Kernel Principal Component Analysis, KPCA)的公式推導過程(轉載)
線性不可分 itl 專註 out center forest 測試 重要 原因 KPCA,中文名稱”核主成分分析“,是對PCA算法的非線性擴展,言外之意,PCA是線性的,其對於非線性數據往往顯得無能為力,例如,不同人之間的人臉圖像,肯定存在非線性關系,自己做的基於ORL數據
SVM公式推導筆記
svm width org sin .org 參考資料 zhang www http 參考資料: 對偶函數-http://blog.pluskid.org/?p=702 KTT和拉格朗日乘子-http://www.cnblogs.com/zhangchaoyan
反向傳播算法(過程及公式推導)
不能 簡化 會有 geo 之前 代碼 求和 不同 eof 一、反向傳播的由來 在我們開始DL的研究之前,需要把ANN—人工神經元網絡以及bp算法做一個簡單解釋。關於ANN的結構,我不再多說,網上有大量的學習資料,主要就是搞清一些名詞:輸入層/輸入神經元,輸出層/輸出神經元,
機器學習之支持向量機(一):支持向量機的公式推導
根據 監督式 art 通用 利用 哪些 這就是 在線 方法 註:關於支持向量機系列文章是借鑒大神的神作,加以自己的理解寫成的;若對原作者有損請告知,我會及時處理。轉載請標明來源。 序: 我在支持向量機系列中主要講支持向量機的公式推導,第一部分講到推出拉格朗日對偶函數的對偶因
POJ 3026 Borg Maze(Prim+bfs求各點間距離)
spa () 去掉 ets size har href http int 題目鏈接:http://poj.org/problem?id=3026 題目大意:在一個y行 x列的迷宮中,有可行走的通路空格’ ‘,不可行走的墻’#&rsqu
B.儲物點的距離
bject itl ++ 會有 c++ 限制 subject 空間 body 時間限制:C/C++ 1秒,其他語言2秒 空間限制:C/C++ 131072K,其他語言262144K 64bit IO Format: %lld 題目描述 一個數軸
最速降線問題公式推導
關系 工作 第一個 int sub dash calc quad 證明 以前對物理特別感興趣的時候就專門研究過一段時間的變分法,記得當時閱讀了一本十分不錯的書籍,其作者名挺有趣的—老大中先生的《變分法基礎》(真的很不錯的一本講變分法的書,有興趣的同學可以去看
機器學習 LR中的參數叠代公式推導——極大似然和梯度下降
jpg blog 我們 應該 圖片 最大似然 gpo 機器學習實戰 pos 機器學習 LR中的參數叠代公式推導——極大似然和梯度下降 Logistic本質上是一個基於條件概率的判別模型(DiscriminativeModel)。
線性回歸 及 正則化 公式推導
tail 損失函數 csdn .net net nbsp art 公式推導 模型 基礎公式: ?BA/?A = BT ?ATB/?A = B ?ATBA/?A = 2BA 模型函數: hθ(x) = xθ 無正則化損失函數: J(θ) = 1/2(Xθ-Y)2
貝葉斯公式推導
樣本 條件樣式 區別 str 假設 分享 們的 圖片 繼續 基本概念 樣本空間:{試驗所有可能結果}-->一個試驗所有可能結果的集合,用 Ω 表示。所以P(Ω) = 1 事件:樣本空間的一個子集。用A、B、C表示。 條件概率 其實