樹狀陣列的引入

相信讀者一定知道什麼是字首和，形如一串數\(a1,a2...,an,sum[i]=a[1]+a[2]+...+a[i]\)
字首和在演算法的優化上佔有很重要的地位，一般就會預先對資料進行預處理運算以後，再在運算過程中用\(O(1)\)時間呼叫，這樣的操作很大程度上避免了實際運算中的列舉，NOIP2016魔法陣就是一個典型的例題。

But字首和也有其缺陷：

當原序列中的資料修改後如果快速呼叫字首和？？

在此，我們引入了一個名叫樹狀陣列的演算法，快速將單點修改和區間查詢優化到\(O(logn)\)級別。

lowbit的含義

\(lowbit(i)\)表示非負整數i再二進位制下最低位1以及末尾0的個數。

例如，二進位制\(1001001100\)中，\(100\)的長度為\(3\)，所以這個數字\(lowbit\)運算的結果為\(3\)。

根據計算機（dev-c++）的運演算法則可得，lowbit(i)=i&-i .

樹狀陣列的字首和儲存方式

對於每一個求和陣列\(c[i],c[i]\)的求和範圍\(a[i-lowbit(i)+1]\)~\(a[i]\)

用一幅圖可以形象直觀的解釋其儲存方式：

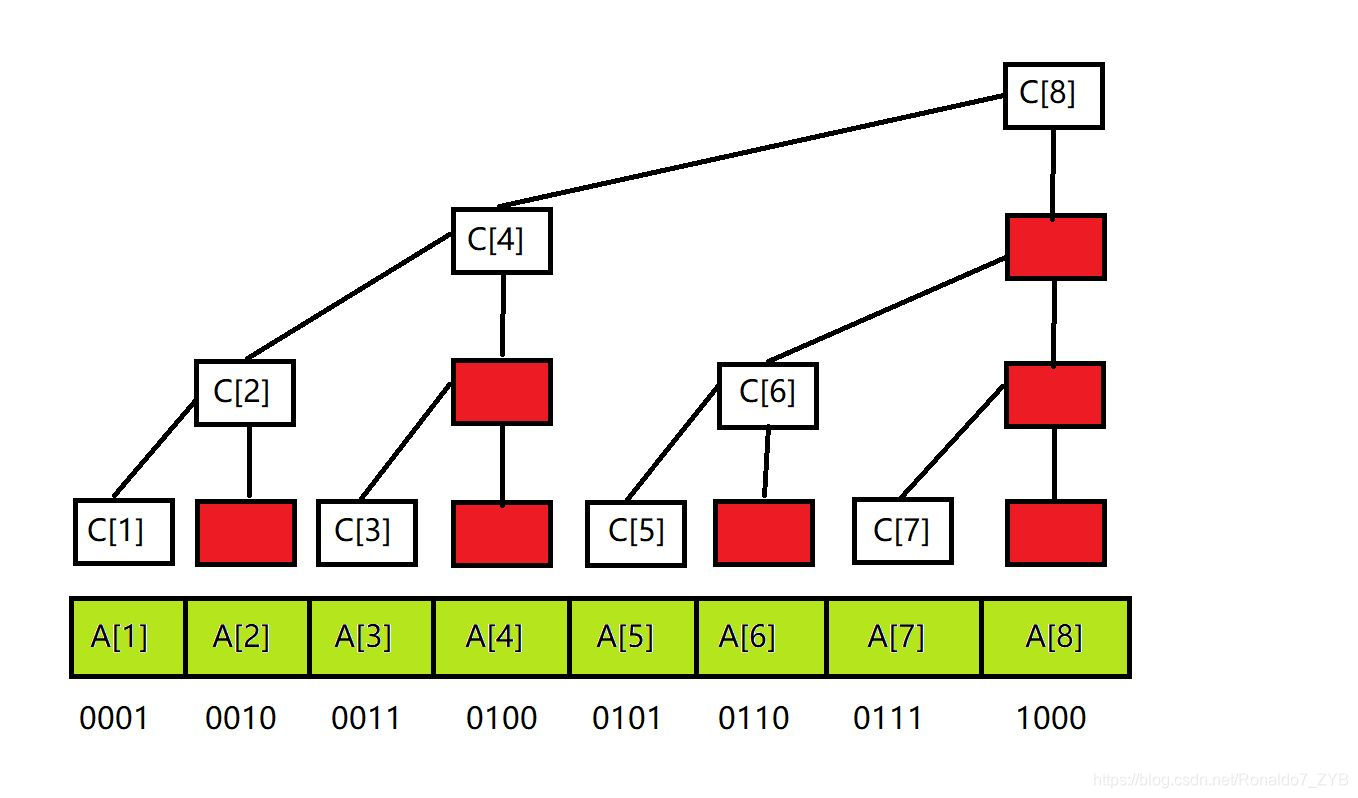
單點修改

對於\(add(x,val)\)，表示\(a[x]\)加上了數值\(val\)。如何修改：

例如\(x=3\)，需要修改的是\(3,4,8\)（若\(n=8\)）

可見對於每一個修改的位置\(x\)，下一個要修改的是\(x+lowbit(x).\)

即，\(3+lowbit(3)=4,4+lowbit(4)=8.\)

故得到程式碼如下：

void add(int x,int val)
{
    for (int i=x;i<=n;i+=lowbit(i))
        c[i]+=val;
    return;
}

區間查詢

\(ask(x)\)表示要查詢\(1\)~\(x\)的字首和。

例如\(x=7，sum=c[7]+c[6]+c[4],\)

可見對於每一\(x\)，下一步要累加的是\(c[x-lowbit(x)].\)

因此得到程式碼如下：

inline int ask(int x)
{
    int ans=0;
    for (int i=x;i>=1;i-=lowbit(i))
        ans+=c[i];
    return ans;   
}

對於查詢l到r區間的和，則\(sum=ask( r )-ask( l-1 ).\)

初始化

每一個\(c\)陣列的求和範圍是\(i-lowbit(i)+1\)~\(i,\)

可以利用最普通的字首和直接求出\(1-i\)的和，

則\(c[i]=sum[i]-sum[i-lowbit(i)]\)。

模板例題——樹狀陣列基本操作

如題，已知一個數列，你需要進行下面兩種操作：

1.將某一個數加上x

2.求出某區間每一個數的和

操作1： 格式：1 x k 含義：將第x個數加上k

操作2： 格式：2 x y 含義：輸出區間[x,y]內每個數的和

輸出包含若干行整數，即為所有操作2的結果。

注意n≤500000.

code：

#include<bits/stdc++.h>
using namespace std;
const int maxn=500000;
int n,m;
int a[maxn+10];
int c[maxn+10];
int sum[maxn+10];
#define lowbit(x) (x&-x)
void add(int x,int val)
{
    for (int i=x;i<=n;i+=lowbit(i))
        c[i]+=val;
    return;
}
inline int ask(int x)
{
    int ans=0;
    for (int i=x;i>=1;i-=lowbit(i))
        ans+=c[i];
    return ans;   
}
int main()
{
    scanf("%d%d",&n,&m);
    for (int i=1;i<=n;++i) 
    {
        scanf("%d",a+i);
        sum[i]=sum[i-1]+a[i];
    }
    for (int i=1;i<=n;++i) c[i]=sum[i]-sum[i-lowbit(i)];
    for (int i=1;i<=m;++i)
    {
        int num,x,y;
        scanf("%d%d%d",&num,&x,&y);
        if (num==1) add(x,y);
        else printf("%d\n",ask(y)-ask(x-1));
    }
    return 0;
} 

差分——區間修改

已知一個數列，你需要進行下面兩種操作：

1.將某區間每一個數數加上x

2.求出某一個數的值

操作1： 格式：1 x y k 含義：將區間[x,y]內每個數加上k

操作2： 格式：2 x 含義：輸出第x個數的值

注意n≤500000.

對於某一區間\(x~y\)加上\(k\)，可以用一個數組b標記：\(b[x]\)加上\(k\)，\(b[y+1]\)減去\(k\)。

仔細思考一下，其實十分巧妙：

對這個標記陣列做字首和，做到\(x\)及以後剛剛加上了k，但是做到\(y+1\)以後又減回去了。

因此我們只需要用樹狀陣列去維護這個陣列b的字首和，對於操作\(2\)返回\(a[x]+ask(x)\)即可。

code：

#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) (x&-x)
#define LL long long
const LL maxn=500000;
LL n,m;
LL a[maxn+10];
LL c[maxn+10];
void add(LL x,LL val)
{
    for (LL i=x;i<=n;i+=lowbit(i))
        c[i]+=val;
    return;
}
inline LL ask(LL x)
{
    LL sum=0;
    for (LL i=x;i>=1;i-=lowbit(i))
        sum+=c[i];
    return sum;
}
int main(void)
{
    scanf("%lld%lld",&n,&m);
    for (LL i=1;i<=n;++i)   scanf("%lld",a+i);
    for (LL i=1;i<=m;++i)
    {
        LL t;
        scanf("%lld",&t);
        if (t==1)
        {
            LL x,y,k;
            scanf("%lld%lld%lld",&x,&y,&k);
            add(x,k),add(y+1,-k);
        }
        if (t==2)
        {
            LL x;
            scanf("%lld",&x);
            printf("%lld\n",a[x]+ask(x));
        }
    }
    return 0;
}

備註