來考慮這樣一個線性方程組：$Ax = b$其中 $A \in \R^{m\times n}，x \in \R^{n}，x \in \R^{n}$。

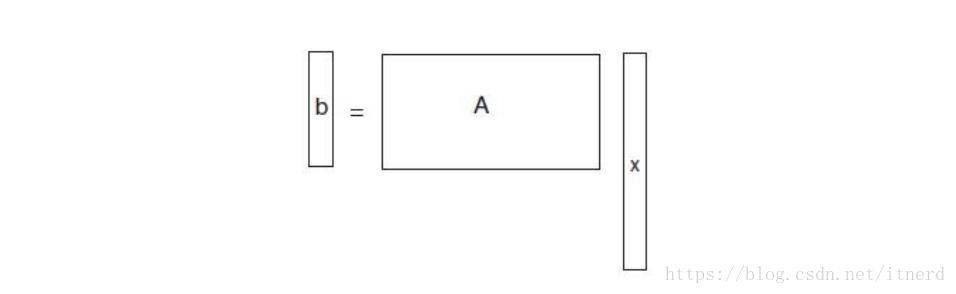
從圖中明顯看出這是一個欠定方程組，因為只要 A 的行滿秩，該方程組有無窮多組解，否則也可能無解（即 b 不在 A 的列空間內，但我們不考慮這種情況）。

這個方程組是怎麼和壓縮感知扯上關係的呢？因為 矩陣A 可以看成一個從 n 維空間到 m 維空間的線性對映，顯然 $n\gg m$，這是一個壓縮對映。

現實的場景是： 採集到的訊號 x 是 n 維的，利用壓縮變換 A 將原訊號壓縮成 m 維的 b，由於 $m$

上面這個方程組 $Ax = b$ 的目的就是利用壓縮的訊號 b，恢復原始訊號 x。

如果你認為這就是一個簡單的求解線性方程組問題的話，那就大錯特錯了，因為如前所述，這個方程組有無窮多個解！

實際上，原始訊號重建問題對應的是一個約束問題： $原始問題：\left\{ \begin{array}{lr} \min ||x||_0, \\ s.t. \:Ax=b \end{array} \right.$

即 在滿足約束 $Ax = b$ 的條件下，經可能地減少 x 中非零元的數目。

不幸的是，上述問題並不是一個凸優化問題，因為 $||\bullet||_0$ 表示非零元個數，不是一個凸函式。

取而代之，我們將優化問題中的目標函式換成 $l_1$ 範數和 $l_2$ 範數來看看，即考慮優化問題： $替代問題1： \left\{ \begin{array}{lr} \min ||x||_2, \\ s.t. \:Ax=b \end{array} \right.$

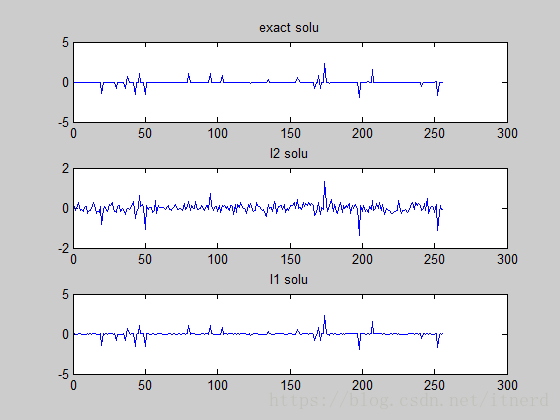
結果如下：

• 圖1 對應原始的稀疏訊號；
• 圖2 對應在$l_2$範數約束下重建的訊號；
• 圖2 對應在$l_1$範數約束下重建的訊號。

從結果可以看出，$l_2$正則化不能保證稀疏性，而 $l_1$正則化可以！

以下是在 matlab 中呼叫 CVX 的 mosek 求解器，對上述 $l_2, l_1$ 約束問題求解的程式碼。

clear all

n = 256;
m = 128;

A = randn(m,n);
u = sprandn(n,1,0.1);
% u = rand(n,1);
b = A*u;

figure(1);
subplot(3,1,1); plot(1:n, u);
title('exact solu');

cvx_solver mosek
cvx_begin 
    variable x(n)
    %minimize( max(norm(x, inf), norm(x,1)/sqrt(n)) )
    %minimize ( max(abs(x)))
    minimize (norm(x))
    subject to
        A*x == b
cvx_end
xl2 = x;

subplot(3,1,2); plot(1:n, xl2);
title('l2 solu');



cvx_begin
    variable x(n)
    minimize( norm(x,1) )
    subject to
        A*x == b
cvx_end
xl1 = x;

subplot(3,1,3); plot(1:n, xl1);
title('l1 solu');

fprintf('\n\nl2 error: %3.2e, l1 error: %3.2e\n', norm(u-xl2), norm(u-xl1));

本文內容參考文再文老師凸優化課程的講義。