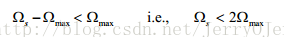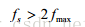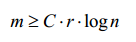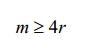一、The Shannon-Nyquist Sampling Theorem

問題：原始資料是連續函式，是否能用有限個取樣百分之百重現原始資料？

夏農回答了這個問題：如果原始資料中最大頻率為f，如果取樣頻率為2f，即每隔1/(2f)秒取一次樣，則可完全恢復原始資料。

陸吾生教授2010年的視訊中給出了非常直觀的解釋：

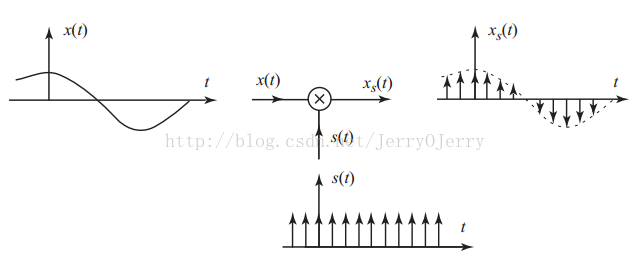
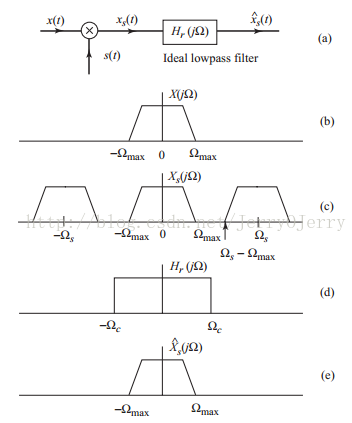
圖a是取樣和恢復過程，圖b表示原始函式的傅立葉變換得到的頻域分佈，圖c表示取樣後的頻域分佈，可以看到是原始頻域分佈複製貼上，且按取樣頻率位移，因為頻率分佈不能重疊，否則資訊就會丟失，這個用公式表示就是下圖的關係，所以可以很容易得到取樣頻率和原始頻率的關係，圖d是低通濾波器，圖e是低通部分，即原始資料的頻率分佈。

最終的恢復公式就是，可以看成是取樣後的訊號與sinc函式卷積的結果：

其中sinc(x)部分是，它的圖示曲線是：

二、Sparse and Compressible Signals

（我的理解）如果訊號是由某種分佈或者幾種分佈構成，則訊號是可以被壓縮的。

比如離散餘弦變換DCT和離散小波變換DWT，本質上即是預先設定的兩組正交基，通過θ=C’x或θ=W‘x即可將原始向量解釋為預設空間中的座標。將θ中接近0的部分設為0，得到θ‘，則轉換後的資料x' = Cθ'或x' = Wθ'，其中C'和W’分別為C和W的轉置。

%Below is a MALAB code to generate matrix DCT. 
function C = gen_dct(n) 
alp = [sqrt(1/n) sqrt(2/n)*ones(1,n-1)]; 
ind = (1:2:(2*n-1))*pi/(2*n); 
C = zeros(n,n); 
for k = 1:n, 
C(k,:) = alp(k)*cos((k-1)*ind); 
end 
 

%Our second example is about an orthonormal basis based on discrete wavelet transform <span style="font-family: Arial, Helvetica, sans-serif; font-size: 12px;">DWT.</span>
% Suppose signal length n= 2^p
%for some integer p, then the basis matrix Wof size nby n
%associated with Daubechies’ orthogonal discrete wavelets can be readily constructed in MATLAB 
%using Toolbox Uvi_Wave toolbox as follows: 
% n -- signal length, must be a power of 2. 
% L -- length of Daubechies wavelet, must be an even integer. 
% W -- orthonormal DWT matrix of size n x n. 
function W = gen_wave(n,L) 
p = log2(n); 
[h0,h1,f0,f1] = daub(L); 
I = eye(n,n); 
W = I; 
for i = 1:n, 
Ii = I(:,i); 
W(:,i) = wt(Ii,h0,h1,p); 
end 
 

上面兩圖為餘弦變換和小波變換的結果，50,100為對應的閾值，可以看出不同的正交基得到的結果不盡相同。

陸吾生教授的視訊裡小波變換講得非常好，想學習的一定要去看看。

三、Sensing a Sparse Signal

小波變換W，θ= W‘x，其實可以理解為用W中基底解釋x的過程，x的稀疏性取決於W基底的”完備性“。這個可以理解為W是一個字典，W中的基底就是字典中的詞，詞越多你對原句的解釋就可以越簡潔，比如”上海“可以解釋為”上“+”海“，也可以解釋為”滬“，因此增加一個矩陣得到[I W]，可以得到更好的稀疏性。字典可以用其他已知的基底構成，比如單位矩陣I，離散餘弦變換DCT，離散小波變換DWT，離散傅立葉變換DFT，Hadamard-Walsh矩陣等等。

現在問題變為Dθ= x，D是n*l的字典，θ是l*1的解，x是輸入向量，如何找到最稀疏的θ？

Dθ = x其實是一個方程數小於變數數的線性方程組，所以這個方程的解一定是特解加通解的形式，特解是類似於廣義逆的形式，θ1 = D‘inv(DD')x，通解需要對D進行SVD分解D=UΛV，U是n*n的特徵向量矩陣，Λ是n*l特徵值矩陣，V是l*l的特徵向量矩陣，θ2 = Vn*δ，Vn是V後(l-n)列，即l*(l-n)的矩陣，δ是(l-n)*1的自由變數（隨便是啥），問題就變成了如何選擇δ確定的解空間中尋找最稀疏的θ1+θ2。

最優化問題形式化為：

其中0-norm表示θ中非0元素的個數，可是這個問題是NP-hard問題，不過可以轉化為：

1-norm就是絕對值的和，上面問題就可以轉化為另一個不帶絕對值的線性規劃問題，這個問題可以用sedumi這個工具求解（具體過程請看陸教授的視訊），得到的解比直接用DWT要好很多。

四、Compressed Sensing

按照夏農的理論，假設取樣頻率為f=n，則一秒鐘需要取樣n個數據，從線性代數的角度來看，是將無限維原始資料對映到n維正交空間。DCT和DWT或者他們構成的字典提供了巧妙的正交基，使得新向量變得稀疏。現在有個想法，為什麼不直接取樣到好空間？換句話說，能否在取樣時不是按照原始資料的頻率，而是按照原始資料資訊的頻率。

假設訊號在Ψ空間中是r-sparse，轉化為壓縮訊號θ：

現在有另外一個空間Φ，取樣x：

Φ^{\hat}是Φ隨機抽取m行的結果，y是m*1，Φ^{\hat}是m*n，x是n*1，m<n，所以這裡是壓縮取樣。

已知y重建x的過程就是最優化一個最稀疏的θ，然後用上面的公式求出x

當m滿足下面公式時，可以保證訊號可以恢復：

可以簡化為：

壓縮感知的Matlab tool可以用CalTech的l1-MAGIC。

Ψ的選擇很重要，直接確定原始資料中哪些資訊是noise哪些是真實資訊，也就是決定訊號是否可以壓縮以及壓縮後是否可以恢復，Φ可以是隨機的矩陣。