字串的全排列和所有組合問題及打靶問題
轉自:https://blog.csdn.net/a1937935900/article/details/77103955
問題1 :輸入一個字串,打印出該字串中字元的所有排列。例如輸入字串abc,則輸出由字元a、b、c所能排列出來的所有字串abc、acb、bac、bca、cab和cba。
思路:這是個遞迴求解的問題。遞迴演算法有四個特性:(1)必須有可達到的終止條件,否則程式將陷入死迴圈;(2)子問題在規模上比原問題小;(3)子問題可通過再次遞迴呼叫求解;(4)子問題的解應能組合成整個問題的解。
對於字串的排列問題。如果能生成n - 1個元素的全排列,就能生成n個元素的全排列。對於只有1個元素的集合,可以直接生成全排列。全排列的遞迴終止條件很明確,只有1個元素時。下面這個圖很清楚的給出了遞迴的過程。
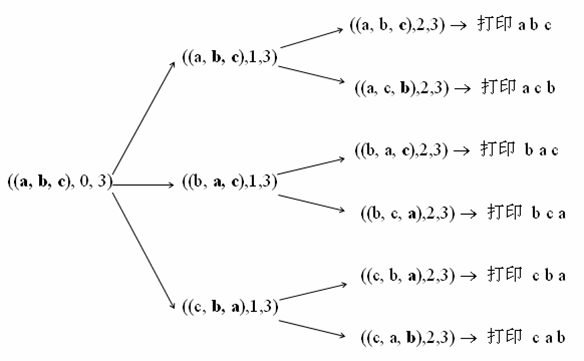
參考程式碼:解法1通過Permutation_Solution1(str, 0, n); 解法2通過呼叫Permutation_Solution2(str, str)來求解問題。
1 //函式功能 : 求一個字串某個區間內字元的全排列 2 //函式引數 : pStr為字串,begin和end表示區間 3 //返回值 : 無 4 void Permutation_Solution1(char *pStr, int begin, int end) 5 { 6 if(begin == end - 1) //只剩一個元素 7 { 8 for(int i = 0; i < end; i++) //列印 9 cout<<pStr[i]; 10 cout<<endl; 11 } 12 else 13 { 14 for(int k = begin; k < end; k++) 15 { 16 swap(pStr[k], pStr[begin]); //交換兩個字元 17 Permutation_Solution1(pStr, begin + 1, end); 18 swap(pStr[k],pStr[begin]); //恢復 19 } 20 } 21 } 22 23 //函式功能 : 求一個字串某個區間內字元的全排列 24 //函式引數 : pStr為字串,pBegin為開始位置 25 //返回值 : 無 26 void Permutation_Solution2(char *pStr, char *pBegin) 27 { 28 if(*pBegin == '\0') 29 { 30 cout<<pStr<<endl; 31 } 32 else 33 { 34 char *pCh = pBegin; 35 while(*pCh != '\0') 36 { 37 swap(*pBegin, *pCh); 38 Permutation_Solution2(pStr, pBegin + 1); 39 swap(*pBegin, *pCh); 40 pCh++; 41 } 42 } 43 } 44 //提供的公共介面 45 void Permutation(char *pStr) 46 { 47 Permutation_Solution1(pStr, 0, strlen(pStr)); 48 //Permutation_Solution2(pStr,pStr); 49 }
問題2:輸入一個字串,輸出該字串中字元的所有組合。舉個例子,如果輸入abc,它的組合有a、b、c、ab、ac、bc、abc。
思路:同樣是用遞迴求解。可以考慮求長度為n的字串中m個字元的組合,設為C(n,m)。原問題的解即為C(n, 1), C(n, 2),...C(n, n)的總和。對於求C(n, m),從第一個字元開始掃描,每個字元有兩種情況,要麼被選中,要麼不被選中,如果被選中,遞迴求解C(n-1, m-1)。如果未被選中,遞迴求解C(n-1, m)。不管哪種方式,n的值都會減少,遞迴的終止條件n=0或m=0。
1 //函式功能 : 從一個字串中選m個元素 2 //函式引數 : pStr為字串, m為選的元素個數, result為選中的 3 //返回值 : 無 4 void Combination_m(char *pStr, int m, vector<char> &result) 5 { 6 if(pStr == NULL || (*pStr == '\0'&& m != 0)) 7 return; 8 if(m == 0) //遞迴終止條件 9 { 10 for(unsigned i = 0; i < result.size(); i++) 11 cout<<result[i]; 12 cout<<endl; 13 return; 14 } 15 //選擇這個元素 16 result.push_back(*pStr); 17 Combination_m(pStr + 1, m - 1, result); 18 result.pop_back(); 19 //不選擇這個元素 20 Combination_m(pStr + 1, m, result); 21 } 22 //函式功能 : 求一個字串的組合 23 //函式引數 : pStr為字串 24 //返回值 : 無 25 void Combination(char *pStr) 26 { 27 if(pStr == NULL || *pStr == '\0') 28 return; 29 int number = strlen(pStr); 30 for(int i = 1; i <= number; i++) 31 { 32 vector<char> result; 33 Combination_m(pStr, i, result); 34 } 35 }
問題3:打靶問題。一個射擊運動員打靶,靶一共有10環,連開10 槍打中90環的可能性有多少?
思路:這道題的思路與字串的組合很像,用遞迴解決。一次射擊有11種可能,命中1環至10環,或脫靶。
參考程式碼:
1 //函式功能 : 求解number次打中sum環的種數
2 //函式引數 : number為打靶次數,sum為需要命中的環數,result用來儲存中間結果,total記錄種數
3 //返回值 : 無
4 void ShootProblem_Solution1(int number, int sum, vector<int> &result, int *total)
5 {
6 if(sum < 0 || number * 10 < sum) //加number * 10 < sum非常重要,它可以減少大量的遞迴,類似剪枝操作
7 return;
8 if(number == 1) //最後一槍
9 {
10 if(sum <= 10) //如果剩餘環數小於10,只要最後一槍打sum環就可以了
11 {
12 for(unsigned i = 0; i < result.size(); i++)
13 cout<<result[i]<<' ';
14 cout<<sum<<endl;
15 (*total)++;
16 return;
17 }
18 else
19 return;
20 }
21 for(unsigned i = 0; i <= 10; i++) //命中0-10環
22 {
23 result.push_back(i);
24 ShootProblem_Solution1(number-1, sum-i, result, total); //針對剩餘環數遞迴求解
25 result.pop_back();
26 }
27 }
28 //提供的公共介面
29 void ShootProblem(int number, int sum)
30 {
31 int total = 0;
32 vector<int> result;
33 ShootProblem_Solution1(number, sum, result, &total);
34 cout<<"total nums = "<<total<<endl;
35 }
